BUSINESS BOOKS

應用舉例

13-1　例1

暖通空調製造商為暖氣設備、通風設備和空調行業生產零部件與原材料，其中一家工廠為家居建材市場生產不同尺寸的金屬管道。有一種產品是直徑為6英寸的金屬管道。這是一個很簡單的產品，但產品的直徑是很關鍵的一個指標。如果它太大或太小，都會造成建築工人難以將這個管道與系統中其他部分匹配起來。精確的尺寸是6英寸，可接受的波動範圍是±0.3英寸。任何在此範圍外的產品都是殘次品。生產線的檢查人員發現實際產品的直徑是5.99英寸，標準差是0.01英寸。

a.這一過程的能力指數是多少？生產一件殘次品的概率是多少？

b.生產線的檢查人員認為他可以不改變過程波動，就能通過調整過程以改變直徑的均值，使其與目標直徑一致。如果他能做到這一點，那麼能力指數會是多少？在這調整後的過程中，生產一件殘次品的概率是多少？

c.通過對員工進行更好的培訓和設備升級的投資，公司能夠實現產品直徑的均值與目標均值一致，並且標準差為0.005英寸。如果能夠實現這一目標，那麼能力指數將會是多少？生產出一件殘次品的概率將是多少？

解答

這一過程是不滿足條件的。能力指數是基於LSL的，表明過程的均值要比目標值低。

為了求得生產一件殘次品的概率，我們需要先找到LCL和USL的Z值：

即2.275%的產品都會太小。

過大的概率是1-0.999 968=0.000 032，因此會有0.003 2%的產品太小。

生產出殘次品的概率是0.022 75+0.000 032=0.022 782，因此2.278 2%的產品會是殘次品。從數量上來看，每100萬件產品中會有22 782件產品是殘次品。

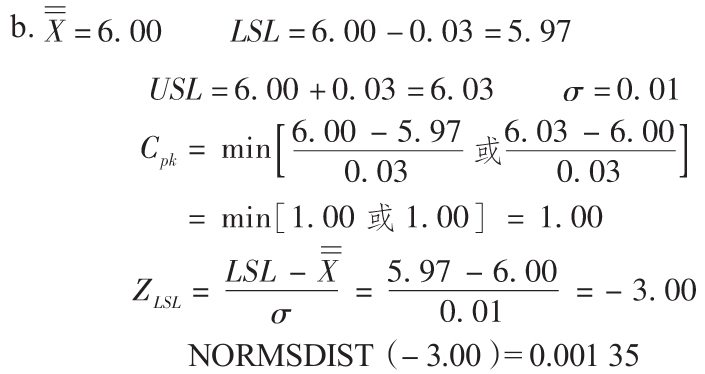
即只有0.135%的產品會太小。

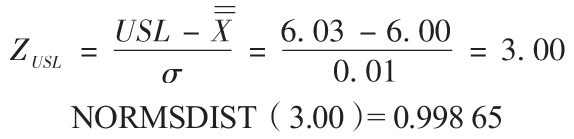
過大的概率是1-0.998 65=0.001 35，因此會有0.135%的產品會太大。

生產出殘次品的概率是0.001 35+0.001 35=0.002 7，因此0.27%的產品會是殘次品。從數量上來看，每100萬件產品中會有2 700件產品是殘次品。通過調整過程的均值，使殘次品的產出降低了90%。

由於過程的均值與目標值是一致的，且規範限制與過程均值有3個標準偏差的距離，因此這一調整過程的能力指數Cpk =1.00。為了要比此方式更好地實現目標，我們需要減少過程的波動，正如c部分那樣。

通過將過程標準差減半，實現了過程能力指數翻了1倍。這對產出的殘次品率有什麼影響呢？

按照前面的思路，生產出一件殘次品的概率是0.000 000 001 973，這一概率非常小！利用前面的數字例子，每100萬件產品中只有0.001 973件殘次品。通過將過程標準差降低一半，我們可以實現殘次品出現概率降低，這一降低比例遠超於50%，本例中是通過管道直徑來判斷是不是殘次品。這一例子證明了六西格瑪質量概念的強大和重要性。

13-2　例2

每天對一家保險公司的某一部門填寫好的表格進行抽樣，以檢查這一部門的工作質量。為了給這個部門制定一個試驗性規範，在15天中每天抽取一個容量為100單位的樣本，其結果如下表所示。

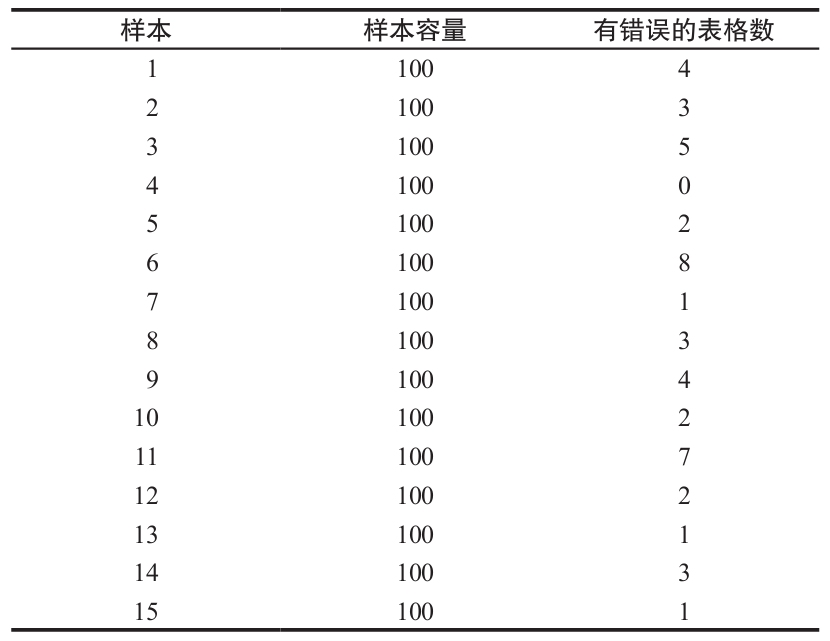
a.在95%的置信度區間下繪製一個p圖（z=1.96）。

b.畫出這15個樣本點。

c.你如何評價該過程？

解答

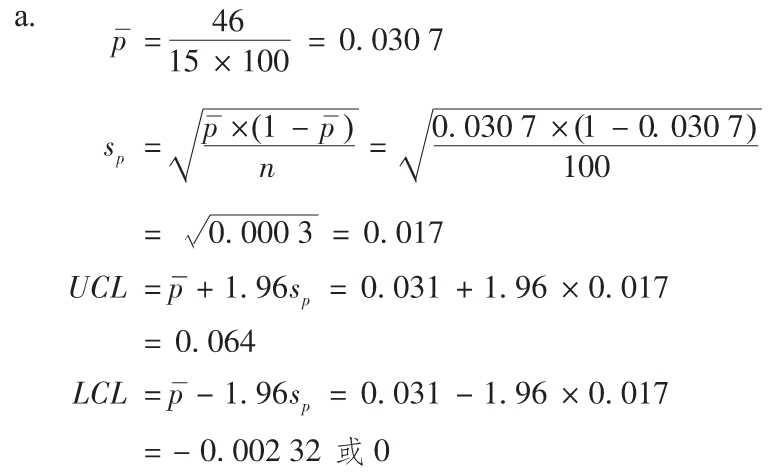
b.缺陷點圖示如下。

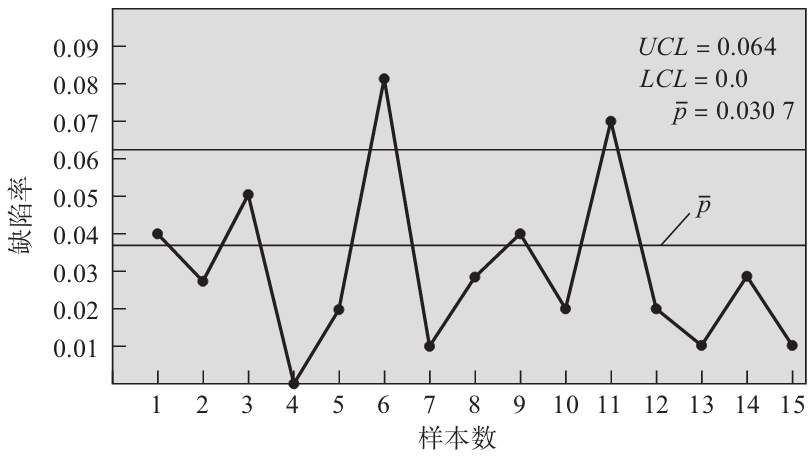
c.在15個樣本中，有2個超出了控制界限。由於控制界限設定為95%，即1/20，因此我們認為該過程失控。需要對其進行檢查，找出如此巨大波動的原因。

13-3　例3

管理者試圖確定以3%的缺陷率穩定生產的零件A是否需要檢測。如果不進行檢測，這3%的缺陷品將通過產品裝配階段，在後面的階段被更換掉。如果檢測所有的零件，1/3的缺陷品將會被發現，因此質量水平提升到2%的缺陷率。

a.如果每單位檢測成本為0.01美元，在最後裝配時替換一個次品的成本為4.00美元，是否應該進行檢測？

b.假設每單位檢測成本為0.05美元而不是0.01美元，問題a的答案是否會變化？

解答

是否應該檢測零件A？

無檢測缺陷率為0.03。

有檢測缺陷率為0.02。

a.只要簡單地計算1%提升帶來的效果，很容易解決問題。

收益=0.01×4.00=0.04（美元）

檢測成本=0.01（美元）

因此，進行檢測，每單位節約成本0.03美元。

b.單位檢測成本為0.05美元，比檢測節約的成本高0.01美元。因此不應進行檢測。