e4 Robert Jacobs 運營管理 v15
13.1 統計質量控制
本章內容涉及統計質量控制 (statistical quality control,SQC),主要講述質量管理的定量分析方法。通常SQC是從一致性角度評估質量的一些技術方法。它需要進行定期的過程抽樣和數據統計分析,從而評估出我們提供的產品和服務與其設計要求之間的吻合程度。
如下面的例子所示,SQC可以應用在物流、製造和服務過程中。
·汽車噴漆缺陷數量的控制,安裝一個新的噴嘴是否可以提升噴漆質量?
·在基於Web的交易系統中執行訂單的時間控制,安裝一臺新的服務器是否可以提升服務,在交易日裡系統績效是否有變化?
·我們對3英寸滾珠軸承的裝配尺寸公差進行控制,給定軸承的製造工藝,每生產100萬個預計會產生多少個缺陷產品?
·在中午繁忙時間段,通過免下車窗口服務一位顧客需要多長時間?

在中國深圳的美泰實驗室裡,ELMO舞蹈小雞玩偶正在接受聲音檢查。美泰公司正遊說其實驗室為玩具安全性提供檢測證明。這家加州公司在6個國家擁有10個實驗室。
製造和服務流程的輸出結果通常都會出現一些波動。多種因素可以導致這種波動,其中有些因素是可以控制的,有些因素是流程所固有的。那些可以被識別和控制的因素導致的波動稱為非隨機波動 (assignable variation)。例如,由於工人的培訓不一致導致的波動和由於機器調試不當導致的波動都是非隨機波動。流程固有的因素所導致的波動叫正常波動 (common variation),通常稱為隨機波動。
正如本節的標題所示,我們需要了解基本的統計知識。回憶一下正態分佈的均值和標準差的定義。其中,均值是指一組數據的平均值。其數學表達如下:

式中xi ——觀測值;
n——觀測值的總數。
標準差是:

注:原書疑有誤,更正為此。——譯者注
應用SQC進行過程監控時,過程輸出結果被隨機抽樣並進行統計計算。樣本的統計分佈與流程本身的統計分佈具有類似的變化規律,只是樣本的統計方差會較小。因此,它可以快速診斷出真實流程分佈的變化,抽樣的目的是識別出非隨機的變化何時產生,進而確定變化產生的根源。
在SQC術語中,西格瑪(σ)是指樣本標準差,根據分佈特點不同(比如,正態分佈或者泊松分佈)西格瑪的計算方法也不相同。
13.1.1 理解並測量過程變化
人們普遍認為,減少變異可以提升質量。直觀的理解是:如果火車總是可以保持準時,那麼列車時刻表就可以制定得更加精確;如果服裝尺寸是一致的,可以降低通過從目錄中訂購的時間。但是人們很少考慮降低這些可變性所帶來的價值。在設計一個機械設備(如汽車)的時候,相關知識被明確地定義。活塞必須適合汽缸,門必須適合門框,電氣部件必須兼容,輪胎必須能夠承擔所需的負載,等等。否則,質量將無法接受,客戶將不滿意。
然而,工程師也知道不可能有零變異性。由於這個原因,設計人員建立了規範,不僅定義了目標值,而且還定義了可接受的範圍限制。例如,如果一個尺寸的目標值是10英寸,那麼設計規範可以是10±0.02英寸。這將告訴製造部門,雖然它應該追求10英寸,但是9.98~10.02英寸都是可以接受的。這些設計限制通常被稱為規範上限和下限 (upper and lower specif ication limits)。
如圖13-1所示,傳統觀念認為只要規範參數落在可接受的範圍內,那麼就認為這些零件的質量是好的,而且都是一樣好;如果是落在可接受範圍之外,則認為這些零件的質量都是壞的(這裡要注意,在可接受範圍內的質量成本都是0,一旦超出這個範圍就會產生一定數額的質量成本)。
來自日本的知名質量專家田口原一(Genichi Taguchi)曾經指出如圖13-1所示的傳統觀念是不合適的,理由如下。
(1)從顧客角度來說,如果兩個產品都在規範界限附近,一個在可接受範圍之內,一個在可接受範圍之外,那麼這兩個產品並沒有什麼差別;相反,同樣是處於可接受範圍之內的兩個產品,如果一個處於目標水平,而另一個處於界限水平,那麼這兩個產品的質量具有明顯差別。
(2)隨著顧客要求越高,降低波動的緊迫性就越大。然而,圖13-1沒有反映這種思想。
田口原一給出了一個更科學的展示損失的圖,如圖13-2所示。注意,在這個圖中成本用一條平滑的曲線來表示。有許多例子可以體現這種觀點:齒輪傳動過程中的齧合、膠片電影的速度、工作間或者百貨商店的溫度,等等。幾乎所有可以被測量的事物,顧客看到的不是一條突變的線條,而是一條接受度隨著偏離目標值的距離漸變的線。相比圖13-1,圖13-2能更好地反映顧客眼中的損失函數。
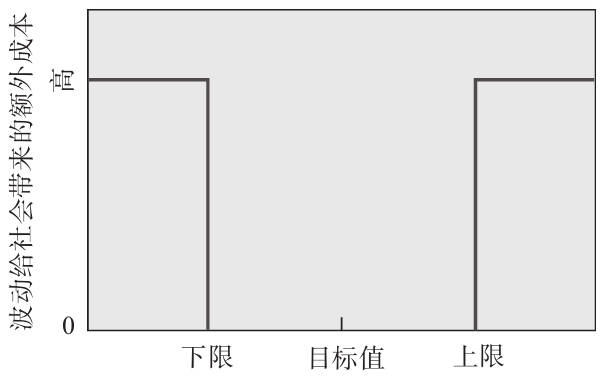
圖13-1 傳統的波動成本的觀點
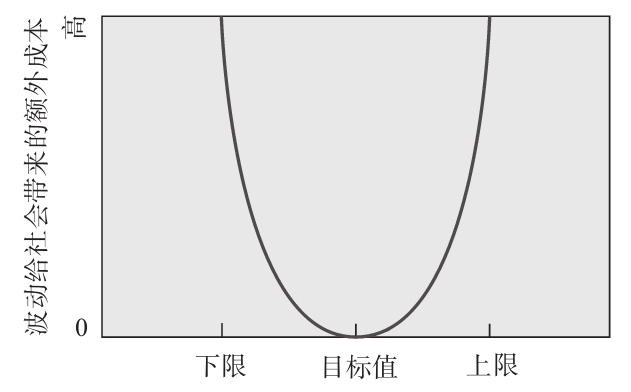
圖13-2 田口原一的波動成本的觀點
當然,如果在規範範圍之外的產品總是做報廢處理,在大多數情況下成本損失曲線會在規範範圍之外變得平坦。這是因為,至少在理論上講,這些產品是不會賣出去的,因此不會給社會造成外部損失成本。然而,在許多實際情況中,要麼就是企業有能力生產相當高比例的符合規範的產品而不需要進行百分之百的檢驗,要麼就是生產的合格品比例不高而需要進行全檢,並對超出界限的產品通過返工返修達標。在任何一種情況下,這種拋物線形損失函數都是一個合理的假設。
13.1.2 測量過程能力
田口原一認為是否在可接受範圍內並非一個是或者不是的判斷,而是一個連續函數。另外,摩托羅拉公司的質量專家認為用於生產產品或者提供服務的過程應該要達到非常高的水平,從而使缺陷的發生概率很低。摩托羅拉採用六西格瑪管理令其過程能力和產品設計聞名於世。 [1] 我們在設計一個零件的時候,就規定某些尺寸必須在規範限定的上下限之內。
舉個簡單的例子,假設我們為一個轉軸設計軸承,比如一個汽車車輪的車軸。這裡會涉及很多變量,比如軸承的寬度、滾子的尺寸、車軸的尺寸、車軸長度、它怎樣得到支撐的,等等。設計者為每個變量設定了限制,以確保這些部分能夠正確地匹配。假設開始選擇了一種設計,其軸承的直徑設為1.250±0.005英寸。這就是說可以接受的軸承直徑在1.245~1.255英寸(分別是規範下限和上限)波動。
接下來考慮一下製造軸承的過程。試想我們可以許多不同的過程來製造軸承。通常在設計製造某一個部件的過程時還要考慮一些權衡。例如,這一過程可能速度非常快但不是很穩定,或者相反,它可能很慢但非常穩定。軸承製造過程的一致性可以通過測量直徑的標準差得到。我們可以這樣進行測試:製造100個軸承並測試樣本中的每個直徑。
我們假設經過測試,發現直徑的均值是1.250英寸。也就是說,這一過程的均值正好位於規範上限和下限的中間。在實際中像我們的例子中這樣恰好居中的過程是很少的。假如說直徑的標準差或者σ等於0.002英寸,這意味著過程生產出的軸承不完全是同一尺寸。
在本章後面我們將會看到,一般我們用控制圖對某生產過程進行監控,比如當這一過程生產的軸承大於或者小於1.250英寸3個標準差(±0.006英寸),就停止該過程。這就是說我們的產品都是在1.244(也就是1.250-3×0.002)和1.256(也就是1.250+3×0.002)英寸之間,其中1.244和1.256就是這一過程所限制的上下界。注意,不要把這裡的術語搞混淆了。“過程”的限制是顯示製造軸承這一過程的一致性如何。管理這一過程的目標是把軸承的直徑保持在均值的上下3個標準差之內。“規範”限制是關於部件的設計。回憶一下,從設計的角度來看,可接受的零件的直徑在1.245~1.255英寸(分別是規範下限和上限)。
關鍵思想 
其重點是該過程應該能夠在設計規範中做好。在這裡,我們將展示如何使用統計數據來評估流程的優異程度。
我們可以看到,過程的界限範圍比設計者規定的規範範圍要稍大一些。這樣並不好,因為我們生產出來的一些零件可能達不到規範要求。採用六西格瑪過程的公司要求過程設計規格界限偏離過程均值6倍標準差。對於軸承生產過程,過程的標準差要達到多小才能夠達到六西格瑪水平?我們的設計規範是1.250±0.005英寸。這裡0.005是指過程的波動,0.005除以6等於0.000 83,我們可以據此來確定六西格瑪過程的標準差。因此要達到六西格瑪標準,這一過程生產出的產品直徑均值要恰好為1.250英寸,而且標準差要小於等於0.000 83英寸。
可能這時有些讀者對六西格瑪的整個思想有點混淆不清了。比如,為什麼我們不對每一軸承進行測試,然後把那些直徑小於1.245英寸和大於1.255英寸的挑出來呢?這當然可以做到,並且有很多零件都是進行百分之百的檢測的。而問題是對於一家每小時要製造成千上萬個零件的公司來說,測量每一個生產出來的零件的每一個關鍵尺寸將是非常昂貴的。對於軸承來說,除了直徑之外,很可能還有10個或者更多其他關鍵尺寸需要測量。如果採用百分之百檢測的方法,公司在檢測上花費的時間可能要比實際製造這些零件的時間還要多。這就是為什麼公司用小樣本進行定期檢測以保證過程是在統計控制之中。我們將在本章後面詳細討論統計抽樣的原理。
當一個過程的均值和標準差可以令過程上下控制界限相對於規範的上下限來說可以接受,那麼我們說一個過程是合格的。圖13-3a是我們在前面討論的過程中軸承直徑尺寸的分佈情況。平均值或者說均值為1.250,設計規範要求的上下限分別是1.245和1.255。過程的控制界限是加減3個標準差(1.244和1.256)。注意,這裡深色的區域表示將會產生缺陷產品的概率。
如果我們可以通過減小軸承直徑的標準差來改進過程,缺陷的概率就會減小。圖13-3b展示了一個標準差減小到0.000 83(淺色區域)的新過程。儘管我們不能從圖中看出該過程仍有可能產生缺陷,但是這個概率將會非常低。
假設過程中心值或者過程均值偏離了均值。如圖13-4所示,過程均值朝著上界的方向偏離了一個標準差。這就會使缺陷期望值升高,但我們看到這樣的過程仍舊很不錯。我們可以用能力指數來衡量一個過程相對於設計要求的滿足水平。關於過程能力的計算將在下一節中詳細描述。
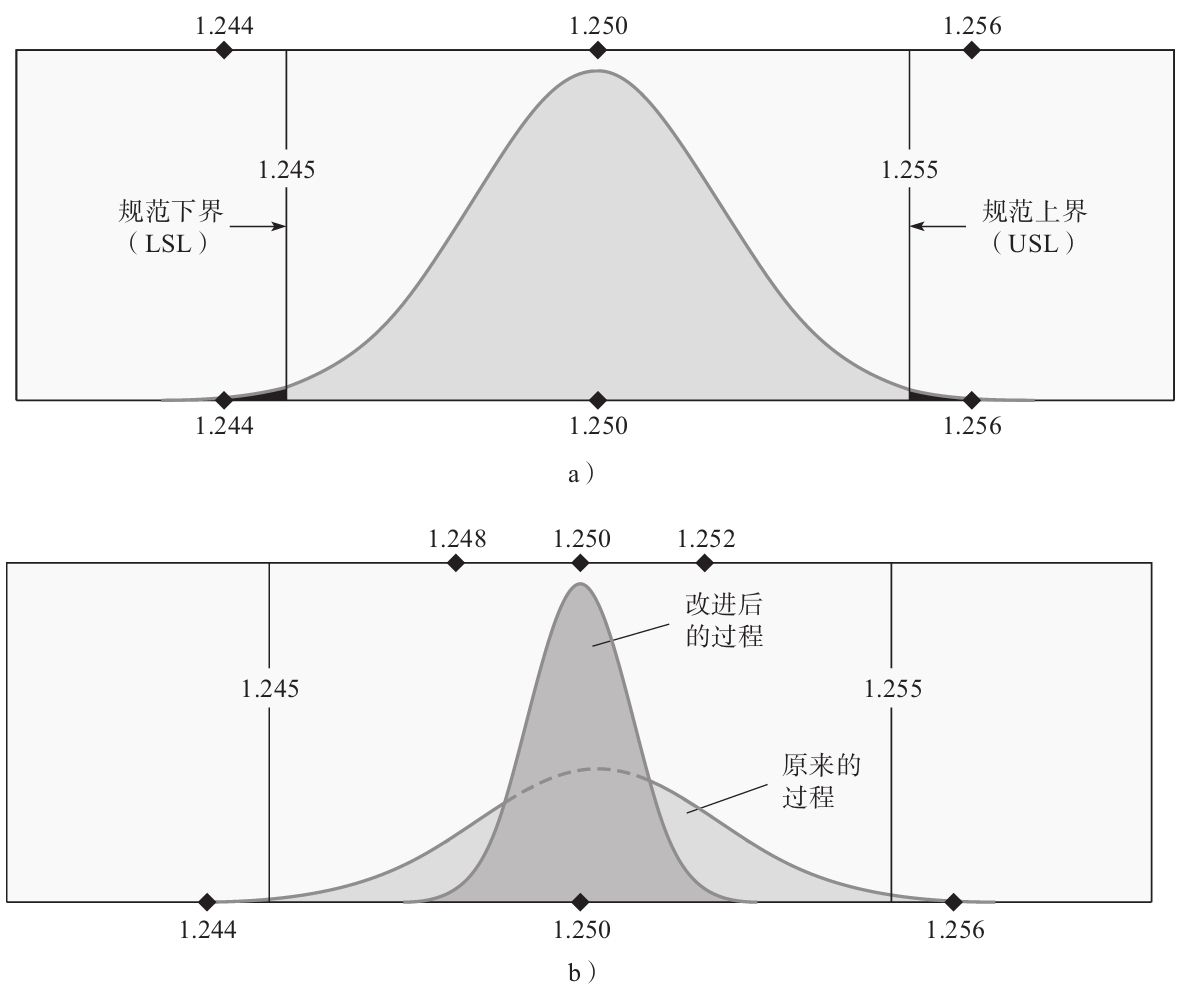
圖13-3 過程能力

圖13-4 過程均值偏離中值的過程能力
過程能力指數
過程能力指數 (capability index,Cpk )表示生產的零件與設計界限規定的範圍的吻合程度。如果設計界限比過程所允許的3σ大,則可以允許過程均值在調試前偏離中心值,即使這樣仍然能夠得到較高的合格率。
根據圖13-3和圖13-4可以看出,過程能力指數(Cpk )是指過程均值及其分佈邊界相對於設計規範的位置。中值偏離程度越大,產生缺陷的概率就越大。
由於過程中值可能向任一方向偏離,所以其偏離方向與設計規範距離就規定了過程能力的界限。偏離的正方向是數字小的方向。
過程能力指數(Cpk )的計算公式如下:

結合在圖13-4中的例子,假設過程均值為1.251且σ=0.000 83(σ代表了標準差):

Cpk=1.6,為最小值。可見,這個過程能力指數相當不錯,缺陷將很少。這告訴我們過程中值偏向右側,與圖13-4所示相似,但是零件參數仍然在設計界限之內。
有時候我們需要計算實際缺陷率。假設過程以某一穩定不變的標準差生產,我們可以應用電子數據表來方便地計算。方法就是根據過程均值和標準差計算產品落在設計規範的上限和下限之外的概率。
計算一下我們的例子,在這個例子中過程是不居中的,均值為1.251英寸,σ=0.000 83,LSL=1.245,USL=1.255,首先我們要用規格的上限和下限來計算Z值。回憶一下所學過的統計學,Z值代表在某一個概率分佈下相對於零點右側或者左側偏離的標準差倍數。

在我們的例子中:

得到這些Z值的一種簡單方法是在Excel中用NORMSDIST函數(你也可以用附錄G中的表格)。這一函數的計算公式為NORMSDIST(Z),其中Z為上面計算得出的Z值。Excel得出如下的值(你得到的結果可能與這裡給出的稍微有些差別,這與你用的Excel的版本有關):
NORMSDIST(-7.228 9)=2.434 61E-13 和 NORMSDIST(4.819 3)=0.999 999 28
要解釋這些數值所表示的信息需要清楚地瞭解NORMSDIST函數給出的具體含義。NORMSDIST得出的是給定的Z值左側的累計概率。Z=-7.228 9是對應於規範下限相對於標準差的倍數,生產出低於這個數的零件概率為2.434 61E-13。
這個數字是用科學記數法,後面的E-13表示我們要把小數點移動13位才能得到真實的缺陷率。因此缺陷率為0.000 000 000 000 243 61,這是一個非常小的數字。同樣,我們計算得到0.999 999 28的零件在規範範圍的上限以下。這裡我們真正感興趣的是大於這個上限的部分,因為那些才是缺陷零件。這一大於規範上限缺陷概率為:1-0.999 999 28=0.000 000 72。
把這兩部分的缺陷率加起來我們得到0.000 000 720 000 243 61。我們可以這樣解釋,即每100萬個零件中預計只有大概0.72件是有缺陷的。顯然這是一個很好的過程。計算了本章後面的習題後你會發現實際情況並不總是這樣。
例13-1
質量保證部門經理在評估一個把壓縮潤滑油裝入氣溶膠罐過程的能力。設計規範要求每罐中平均每平方英寸(psi)的壓強為60磅,且上限為65psi,下限為55psi。他從產品中抽取了一個樣本,發現這批產品平均壓強為61psi,標準差為2psi。這一過程的生產能力如何?產生一個次品的概率有多大?
解答
第一步:對問題中的數據進行闡述。
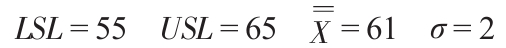
第二步:計算Cpk 。


這不是一個很好的能力指標。我們在第三步中看看為什麼這是正確的。
第三步:計算生產一個缺陷的概率。
罐壓小於55psi的概率:

罐壓大於65psi的概率:

罐壓小於55psi或者大於65psi的概率:
概率=0.001 349 898+0.022 750 132=0.024 100 030
即大約2.4%的氣罐有缺陷。
下表是各種設計界限(以標準差表示)對應的缺陷概率的快速參考表。這個表的假設前提是標準差保持不變並且過程中精確地處於設計界限中間。
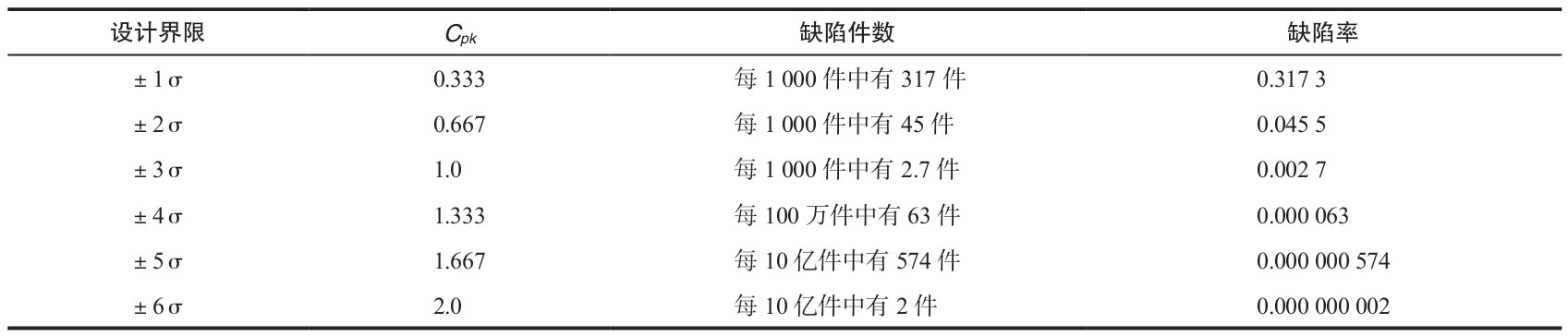
在摩托羅拉的六西格瑪設計界限中,過程偏離均值量為1.5σ(Cpk =1.5),從而實現每生產100萬個產品只有3.4個缺陷。如果均值非常精確位於設計規範界限中間(Cpk =2),那麼預計每10億中只有2個缺陷,如上表所示。
[1] 但因其未能持續關注質量而走向末路。——譯者注