BUSINESS BOOKS

10.3　排隊問題的計算機仿真

一些排隊問題給人的第一印象看似非常簡單，真正做起來卻極其困難或者根本就不可求解。在這裡，我們已經對相互獨立的排隊問題做了討論，也就是說，無論是由單階段構成的整個系統服務還是系列服務中的一個階段服務，它們都是相互獨立的（這種情況發生於當一個服務檯的輸出在下一個服務檯之前允許累計起來，從實質上說，該輸出成為下一個服務的輸入客戶源）。當一系列服務依次進行，且前一個服務的輸出率是後一個服務的輸入率時，我們將不能再運用這些簡單的公式。另外，當問題不能滿足公式規定的條件時，如表10-2規定的條件，也不能運用這些公式。解決這類問題的最好手段是計算機仿真。

排隊問題常常連續地和並行地發生（例如在裝配線和工作車間），通常無法用數學的方法解決。然而，排隊問題通常容易用電子表格仿真。

10.3.1　例題：一條兩階段裝配線

考慮一條所組裝的產品體積很大的裝配線，如冰箱、爐子、汽車、船、電視或傢俱的組裝。圖10-7表示的是一條裝配線上的兩個工作站。

圖10-7　一條裝配線上的兩個工作站

產品的體積是裝配線分析和設計所要考慮的一個重要因素，因為每個工作站上所能存放的產品數量將會影響工人的工作。如果產品體積很大，那麼相鄰的工作站存在著相互依賴關係。如圖10-7所示，鮑勃（Bob）和雷（Ray）在一個兩階段裝配線上工作，鮑勃在工作站1上裝配完的產品傳遞給在工作站2上的雷，雷再進行加工。如果兩個工作站相連，中間沒有存放半成品的地方，那麼如果鮑勃幹得慢，雷就會被迫等待；相反，如果鮑勃幹得快（或者說雷完成工作的時間要比鮑勃長），那麼鮑勃就得等雷。

在這個仿真問題中，我們假設鮑勃是組裝線上的第一個工人，他能夠在任何時候拿到需組裝的半成品進行工作，那麼我們把分析重點放在鮑勃與雷彼此間的相互影響上。

1.研究目標

關於這條裝配線，我們希望能通過研究解決一些問題。下面我們列出了部分待解決的問題：

·每個工人的平均完工時間是多少？

·這條組裝線的生產率是多少？

·鮑勃等待雷的時間是多少？

·雷等待鮑勃的時間是多少？

·如果兩個工作站中間的空間加大，可以存儲半成品，從而增加了工人的獨立性，那麼這對於生產率、等待時間等問題會有什麼影響？

2.收集數據

進行系統仿真，我們需要鮑勃和雷的裝配時間數據。要收集這些數據，一種方法就是將總裝配時間分割成小段時間，在每段時間內對工人進行單獨觀測。對這些數據進行簡單的彙總和分析，我們可以得到非常有用的直方圖。

表10-6顯示的是觀測鮑勃和雷兩人裝配時間後得到的數據表格。為了簡化操作過程，裝配時間以10秒為區間進行劃分。對鮑勃的工作我們進行了100次觀測，而對雷的觀測我們只進行了50次。二者的觀測次數可以不同，但觀測次數越多，時間間隔的劃分越細，則研究的準確性越高。然而，時間間隔越小，觀測次數越多，需要投入的時間和人力也就越多（同時，用於編程的時間和仿真模型運行的時間也就越長）。

表10-6　通過觀測工人得到的數據表格

這種方式的數據收集定義了可以用作仿真的經驗分佈。正如本例中所示的那樣，經驗分佈源自對相關事件的觀察結果。在本例中，觀察的是完成任務的時間。在其他例子中，可觀察到某個時間段內到達排隊系統中的顧客數量、產品需求和服務單個顧客的時間。

對於仿真，某一事件發生的頻率是一個隨機數。這一隨機數與系統中的其他數字完全不相關。附錄H中包括了隨機數表。如需要00～99的隨機數，按照表格中的順序取出從該表中隨機產生一個隨機數。比如56、97、08、31和25是該表中的前5個隨機數。電子數據表格的RAND（）函數可以返回0～1的任一隨機數，函數RANDBETWEEN（minimum，maximum）返回最小值和最大值之間的隨機數。

在本例中，使用了00～99的隨機數。如果某一時間發生概率為10%，需要分配10個數字；如果發生概率32%，則要分配32個數字，如此往復。這樣，隨機數與觀察到的經驗頻率分佈是相匹配的。

表10-7包含了按照實際觀測數據的比率進行分配的隨機數區間。例如，鮑勃在100次操作中有4次在10秒鐘內完成。因此，如果我們用100個數進行分配，那麼我們應該分配4個數與10秒鐘相對應。這4個數可以是任意的，例如42、18、12和93，但是這會使查找工作變得非常煩瑣，所以我們就分配連續數，比如00、01、02和03。

表10-7　鮑勃和雷的隨機數區間

我們得到了50個對雷的觀測的值。我們有兩種方法可以用來分配隨機數。第一種方法是，我們就用50個數（如00～49）來進行分配，並在仿真中忽略掉所有超過49的數。然而，這是一種浪費，因為我們將丟棄隨機數列中50%的數。另一種方法是將頻率次數加倍。例如，我們不是將00～03分配給50次觀測中裝配時間為10秒的4次觀測，而是將00～07分配給100次觀測中的8次觀測，這樣的話，觀測次數加倍了但比例不變。實際上，考慮到當前的計算機速度和本例裝配線的規模，由該方法增加的運行時間是微不足道的。

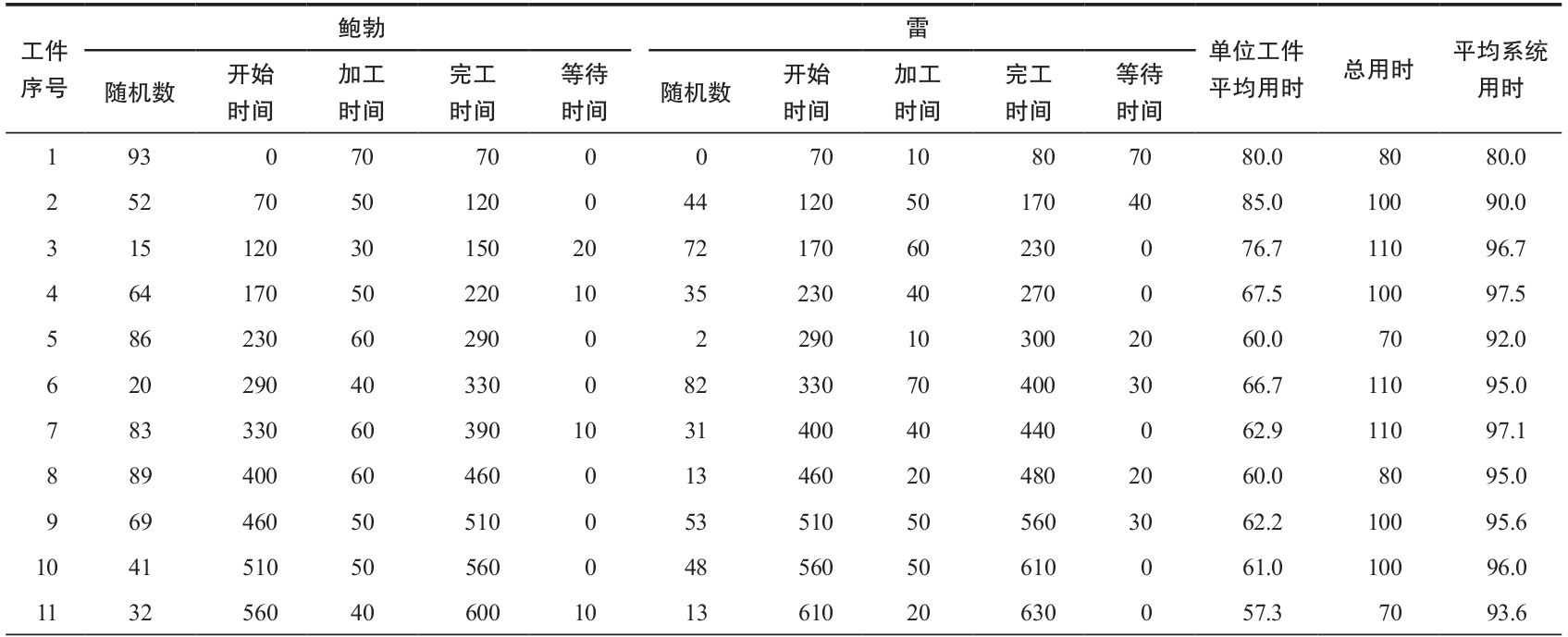
表10-8顯示的是對鮑勃和雷裝配10件產品的手工仿真結果。隨機數來自附錄H，從二位數的第一列開始向下取數。

表10-8　鮑勃和雷：兩階段裝配線的仿真　　（單位：秒）

假設我們從00時間開始，接下來以秒來計算（不要自找麻煩將其換成小時或分鐘）。第一個隨機數56對應於鮑勃第一個裝配工作時間50秒。這個工件傳送給雷，它的開始時間是第50秒。接下來的隨機數是83，根據表10-7，雷用70秒完成了工作。同時，鮑勃開始裝配下一件產品，從第50秒開始用時50秒（隨機數55），在第100秒完成。然而，鮑勃無法開始第三件產品的工作，因為雷在第120秒才做完頭一個工件。因此，鮑勃等了20秒（如果鮑勃與雷的工作站之間有存儲空間，鮑勃幹完的工件可以移出工作站，在第100秒鮑勃就可以做下一個工件）。表裡剩下的數據可以用同樣的方法來計算：得到一個隨機數，找到對應的加工時間，注意等待的時間（如果有的話），並計算完工時間。我們可以看出，由於鮑勃與雷之間沒有存儲空間，兩位工人的等待時間都很長。

現在，我們可以回答一些問題，並且可以對系統進行一些評述，例如：

每件工作的平均加工時間為60秒（總共用時為600秒，平均分配給雷加工的10個工件）。

鮑勃的利用率為470/530=88.7%

雷的利用率為430/550=78.2%（除去最開始的等待時間50秒）

鮑勃的平均加工時間為470/10=47（秒）

雷的平均加工時間為430/10=43（秒）

我們已經說明了怎樣對這個問題進行簡單的手工仿真，但10個抽樣所組成的樣本實在是太小了，不足以保證結果的可信度。因此，這個問題應由計算機進行數千次的重複計算才能得到比較可信的結果（我們將在本章的下一節中對該問題進行進一步擴展）。

對於兩個工人間的存儲空間的研究也是很重要的。解決這個問題，主要是要看在工人之間沒有存儲空間的條件下，流程時間和工人利用率等數據。第二次仿真存儲空間增加一個單位產品，並記錄下相關數據的變化，然後在增加存儲空間2個、3個、4個……的情況下進行仿真。經理可以根據這些數據計算增加存儲空間所增加的成本和使用價值，並將二者加以比較。在工人間增加存儲空間有可能需要一個更大的廠房，系統中需要更多的物料和工件，需要增加物料處理設備、傳送設備，使用更多的熱能和電能，以及增加廠房的維護等。

通過仿真，還可以讓經理知道：如果一個工人被自動化設備所取代，那麼相關數據會有哪些變化。從這個自動化設備裝配線上仿真得到的數據，還可以看出引入自動化設備是否合適。

10.3.2　運用電子表格仿真

在本書裡，我們已經多次提到了電子表格可用於解決許多問題。表10-9就是在Excel電子表格中說明了鮑勃和雷兩階段裝配線的情況。這與我們在表10-8中手工仿真的格式一樣。

表10-9　鮑勃和雷兩階段裝配線在微軟Excel上的仿真　　（單位：秒）

在Excel中總共進行了1 200次仿真（見表10-9），也就是說，雷一共加工了1 200個工件。仿真技術作為一種分析工具，它的動態特性決定了它在定量分析方面具有優勢。解析方法表示的是系統長期運轉的平均結果。我們從

圖10-8a中可以看出有一個明顯的啟動階段（或稱瞬時階段），而從圖中曲線的長期表現中我們可能也會產生疑問，甚至在1 200後，曲線也沒能達到一個常數值（或稱穩定值）。圖10-8a描繪了通過鮑勃和雷兩階段系統的100件的數據。請注意第一個工件完成後的劇烈變化。曲線數據指的是工件完成的平均時間。它是一個累計數據，即第一個工件時間採用的是隨機產生的數值，兩個工件的平均時間是第一次和第二次所用總時間的平均值，而三個工件的平均時間則是前三次所用總時間的平均值，依此類推。曲線的開始階段取決於產生的隨機數據流，因而可以是任何形狀，並不一定如圖所示。我們能夠確定的是加工時間在系統啟動之後的一段時間內將上下波動，直到加工後期，平均加工時間趨於一致。

圖10-8b顯示的是加工工件在系統中的平均時間。在開始階段，曲線在系統中表現出時間不斷增加的趨勢。這是合理的，因為系統從閒置狀態開始，工件從鮑勃到雷的過程中沒有間斷。通常工件進入系統後，在兩個工序間會等待，這使得隨後的工件進入系統的時間不得不延期，從而增加了等待時間。隨著時間的增長，除非第二道工序的工作能力小於第一道，工件傳遞將趨於穩定。在我們當前的案例中，不允許他們之間存在空間。所以，若是鮑勃先完成，他不得不等待雷；反之亦然。

圖10-8c表示的是模擬鮑勃和雷完成1 200個工件產品後的結果。將這些數據與我們手工模擬的10個工件數據相比，手工模擬還不是很差。鮑勃的平均工作時間為46.48秒，這非常接近於長期運行時你所期望的加權平均值，鮑勃工作時間的期望值是（10×4+20×6+30×10×…×）/100=45.9（秒）。雷的工作時間的期望值是（10×4+20×5+30×6×…×）/50=46.4（秒）。

圖　10-8

兩階段裝配線仿真是設計電子表格分析問題的一個很好的例子。在Excel中可以內嵌更多的仿真程序。康奈爾大學運營管理教授約翰·麥克萊恩（John McClain）就開發了兩種仿真電子表格，可以用於說明許多類似的系統。本書的網頁中有這些電子表格。

第一個電子表格叫作“LineSim”，用於分析簡單的序列生產線。這種系統中擁有一系列機器，一臺機器的產品輸出到存儲區，然後成為下一臺機器的輸入產品。這個電子表格可以很容易地設置以適用於不同數量的機器，不同大小的緩衝存儲區和不同處理時間分佈。另外，還可以模仿機器故障和修理的情況。第二個電子表格“CellSim”與前一個相似，但機器的變化適用範圍更加廣泛。我們感謝麥克萊恩教授提供了這些電子表格。

10.3.3　仿真程序和語言

仿真模型可以分為連續型和離散型。連續型模型是基於數學方程建立的，因而是連續的，每一時間點上均有對應值。相反，離散型仿真僅在特定的節點上才運行。例如，對顧客到達銀行的出納窗口這一事件的仿真就是離散型仿真。仿真從一個節點跳到另一個節點：顧客到達、服務開始、服務結束、下一個顧客到達，等等。離散型仿真也可由單位時間（每天、每小時、每分鐘）來引發。這種仿真方法也可以叫作事件仿真。由於前後事件間沒有某種數學聯繫，所以節點之間的點既得不到仿真有效數值也無法得到計算值。運營管理的應用幾乎都採用離散型仿真（事件仿真）。

仿真程序可以分為通用程序和專用程序兩類。通用模式軟件指的是那些允許程序員設計自己的模型。專用模式軟件的仿真程序是專門用於仿真某種特定的應用。再如，在用於製造業的專用仿真中，會考慮到指定的加工中心數量、特性、開工率、加工時間、生產批量、在製品數量、包括人力和加工順序的可用資源等因素。另外，程序還可以讓使用者觀察到動畫，以及在仿真運行時觀察通過系統的數量值和流量值。數據被收集、分析，然後繪製成這些應用類型大都適用的數據表格。命名為ExtendSim的仿真軟件的特徵在專欄10-1中進行了介紹。

|專欄10-1|

動畫和仿真軟件

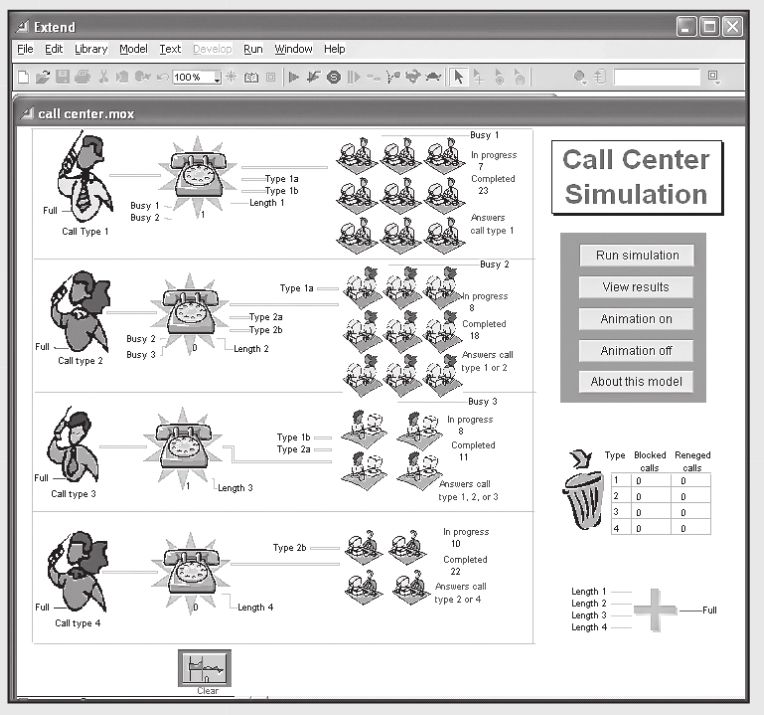
仿真可以很好地應用於呼叫中心。呼叫中心的工作很容易被模擬，而且服務時間、到達頻率、掛斷時間、電話接入呼叫中心的路徑這些信息都很容易獲取。在這個呼叫中心中，有4類電話在隨機間隔時間內到達，呼叫中心有4類接線員可以接線。每個接線員專長於特定的呼叫類型，但是其中一些接線員可以應答不同種類的電話。

我們可以很快地應用Imagine That!公司的產品ExtendSim得到這個仿真。這個產品廣泛運用了動畫，所以可以使讀者能實際地看到呼叫中心運營。你可以訪問下面的網站來更多地瞭解這個產品：http://www.extendsim.com 。

對於仿真軟件我們最後說一點，不要忘記運用電子表格進行仿真。正如你所注意到的，我們在電子表格中仿真了鮑勃和雷的工作流程。在仿真中，電子表格使用起來簡單快捷，這彌補了必須將複雜問題簡單化以適應電子表格的不足。

@RISK是與微軟Excel一起使用的一個加載宏。這個程序給電子表格增加了許多與仿真有關的功能。使用@RISK可以自動地從確定的分佈函數中提取隨機數值，然後自動重算帶入了新隨機數的電子表格，並得到輸出值和統計值。@RISK簡化了建立和運行電子表格仿真的過程。