e4 Robert Jacobs 運營管理 v15
應用舉例
6-2
例1
假設你正在測試求職者能否勝任一條裝配線上的工作。管理部門認為,在操作1 000次後大體上就可以達到穩定狀態。預計普通裝配工人在4分鐘內完成該任務。
a.如果求職者第1次的操作時間為10分鐘,第2次的操作時間為9分鐘,那麼是否應該僱用這個求職者?
b.該求職者第10次操作的預期時間為多少?
c.這一分析的主要限制是什麼?
解答
a.學習率=9/10=90%。
由表6-2可知,第1 000次操作所要求的時間為0.349 9×10=3.449(分鐘),因而應該僱用這個求職者。
b.由表6-2可知,在學習率為90%時,第10次操作的改進因子為0.704 7,因此第10次操作的預期時間為0.704 7×10=7.047(分鐘)。
c.對僱用工人績效的估計需要收集更多的數據。
例2
波音公司收集了它生產的前8架新的商務噴氣式飛機的成本數據。
a.估計新商務噴氣式飛機的學習曲線。
b.估計前1 000架噴氣式飛機的平均生產成本。
c.估計第1 000架噴氣式飛機的生產成本。
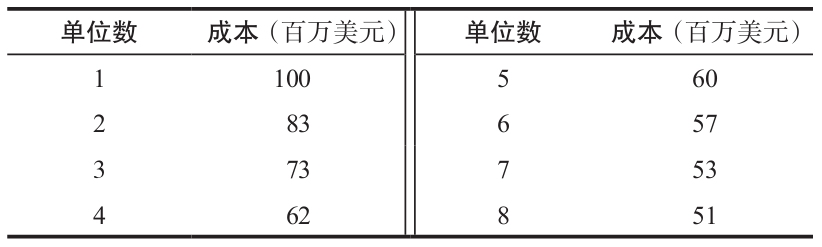
解答
a.首先,通過計算每個雙倍產量的平均學習率估計學習率:
第1架~第2架=83/100=83%
第2架~第4架=62/83=74.7%
第4架~第8架=51/62=82.26%
平均=(83+74.4+82.6)/3=80%
b.從表6-3可以估計出前1 000架飛機的平均成本。在學習率是80%的情況下,第1 000架飛機的改進因子是158.7。前1 000架飛機的製造成本是:
100×158.7=15 870(百萬美元)
前1 000架飛機的平均製造成本是:
15 870/1 000=15.9(百萬美元)
c.用表6-2估計第1 000架飛機的製造成本。在學習率是80%的情況下,第1 000架飛機的改進因子是0.108 2。生產第1 000架飛機的成本是:
100×0.108 2=10.82(百萬美元)