BUSINESS BOOKS

6.2　學習曲線如何建模

有多種方法可以對歷史數據進行分析來描繪一條有用的趨勢曲線。首先我們將使用簡單的指數曲線作為運算程序，然後使用對數進行分析。在算術製表方法中，縱座標為生產單位，一列產品單位數量依次成倍增加，如1，2，4，8，16，…，生產第1個單位產品的時間乘以學習率得到生產第2個單位產品的時間，生產第2個單位產品的時間再乘以學習率將得到生產第4個單位產品的時間，依此類推。因此，如果我們繪製一條80%學習曲線，將得到表6-1中的第2列數字。為便於計劃，通常我們要知道累計直接勞動時間，表6-1中的第3列提供了這方面的信息。第4列即累計平均直接勞動時間，由第3列除以第1列得到（參照下面的部分是如何進行單位計算的）。

表6-1　80%學習曲線所需的單位、累計直接勞動時間、累計平均直接勞動時間

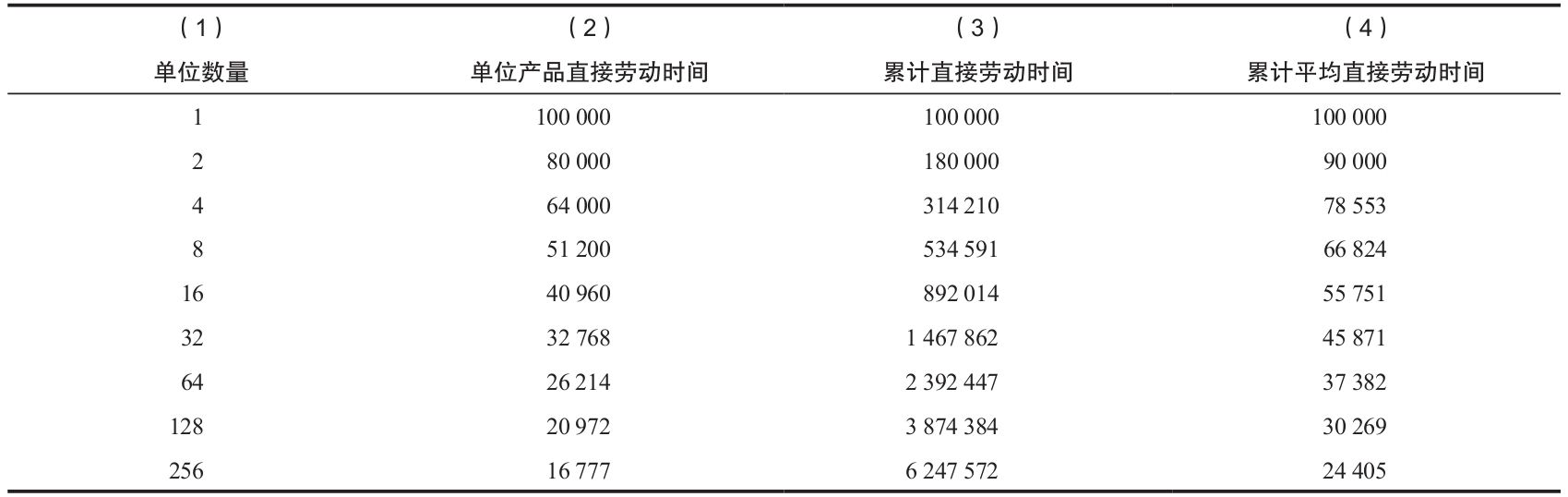
圖6-2a給出了三條不同學習率的曲線，其學習率分別為90%、80%、70%。假定第1個單位產品的生產成本是100美元，第30個單位產品在90%的學習率下的生產成本就是59.63美元，在70%的學習率下的生產成本就是17.37美元。學習率的不同將使結果產生很大差異。

在實踐中，學習曲線經常是在以對數座標刻度的圖上繪製的，其結果是單位產品生產時間學習曲線在整個範圍內都變成了直線，而累計學習曲線在開始的幾個單位之後也變成了直線。線性的好處是有助於預測，並且可以更準確地讀出累計學習曲線。微軟Excel中有這種刻度，在電子表格上簡單地生成一個普通的散點圖，然後選中每一個軸並且使用對數運算。圖6-2b是在對數座標圖上畫出的學習率為80%的單位產品生產成本曲線和平均生產成本曲線。注意，累計平均生產成本曲線在8個單位後就完全變成了直線。

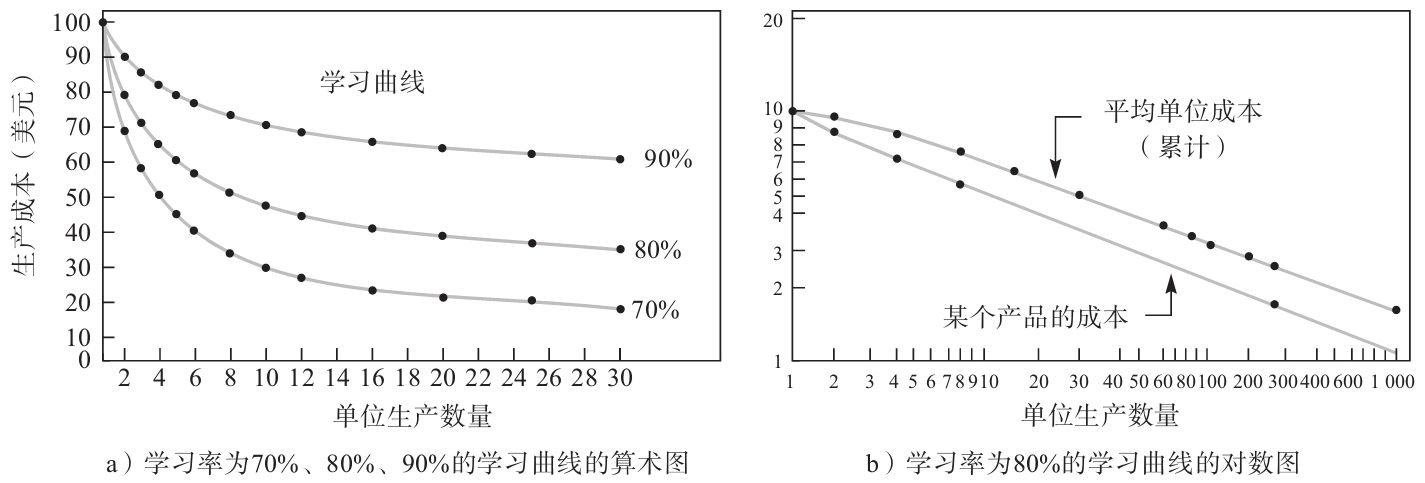
圖6-2　學習曲線的算術圖

雖然算術列表方法很有用，但對學習曲線問題的對數分析方法因為不需要對連續的一系列時間-產量的組合數據進行一一列舉，因而通常比算術列表方法更為有用。而且，在那些數據難以獲得的情況下，對數分析模型可能是獲得估計產出的最佳方法。

6.2.1　對數分析

學習函數的一般形式是：

式中　x——單位生產數量；

Yx ——生產第x個產品所需的直接勞動時間；

K——生產第一個產品所需的直接勞動時間；

n——logb/log2，其中b表示學習率。

這個問題我們可以用數學方法加以求解，也可以用下一節的表格來求解。採用數學方法，為了計算出在我們的例子（表6-1）中生產第8個單位產品所需的勞動時間，我們將以下式計算：

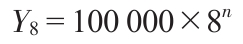
使用對數：

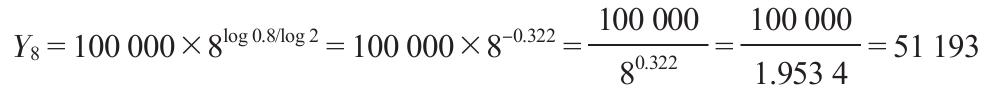
因此，生產第8個單位產品將需要51 193小時。答案可能會有細微差別，可以利用Excel中的公式=100 000×8（log 0.8/log 0.2）得到精確值（見表6-1）。

6.2.2　學習曲線表

已知學習率，利用表6-2和表6-3可以非常方便地估計出某一特定產品或某一組產品的勞動小時數，只需用最初的勞動小時數乘以表中給出的相應值就可以了。獲得單元和累計改進因子的另一種方法是從OSCM Tools應用程序中獲得，該應用程序在http://oscm-pro.com/tools/ 中。

表6-2　學習曲線單位改進因子表

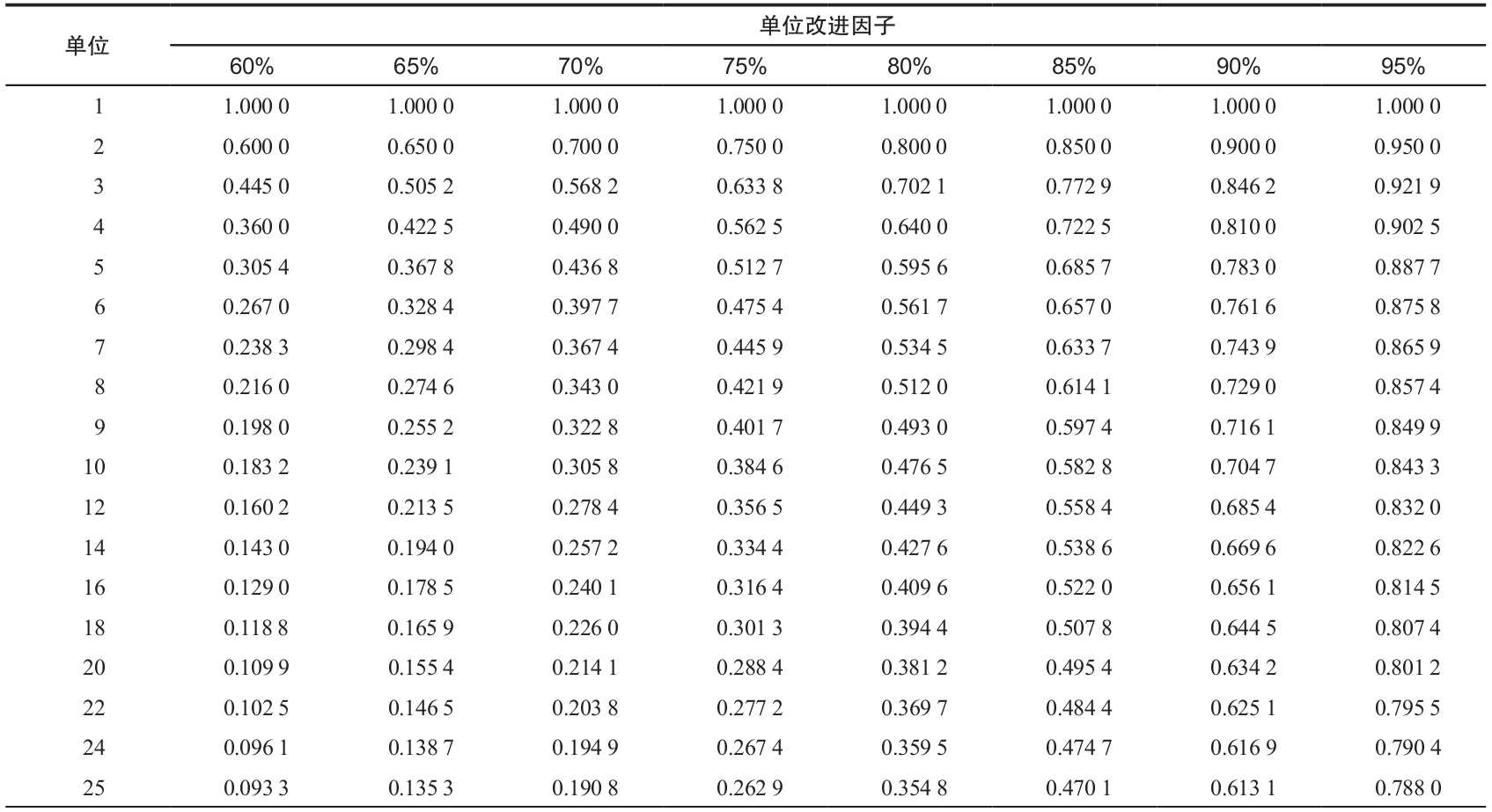
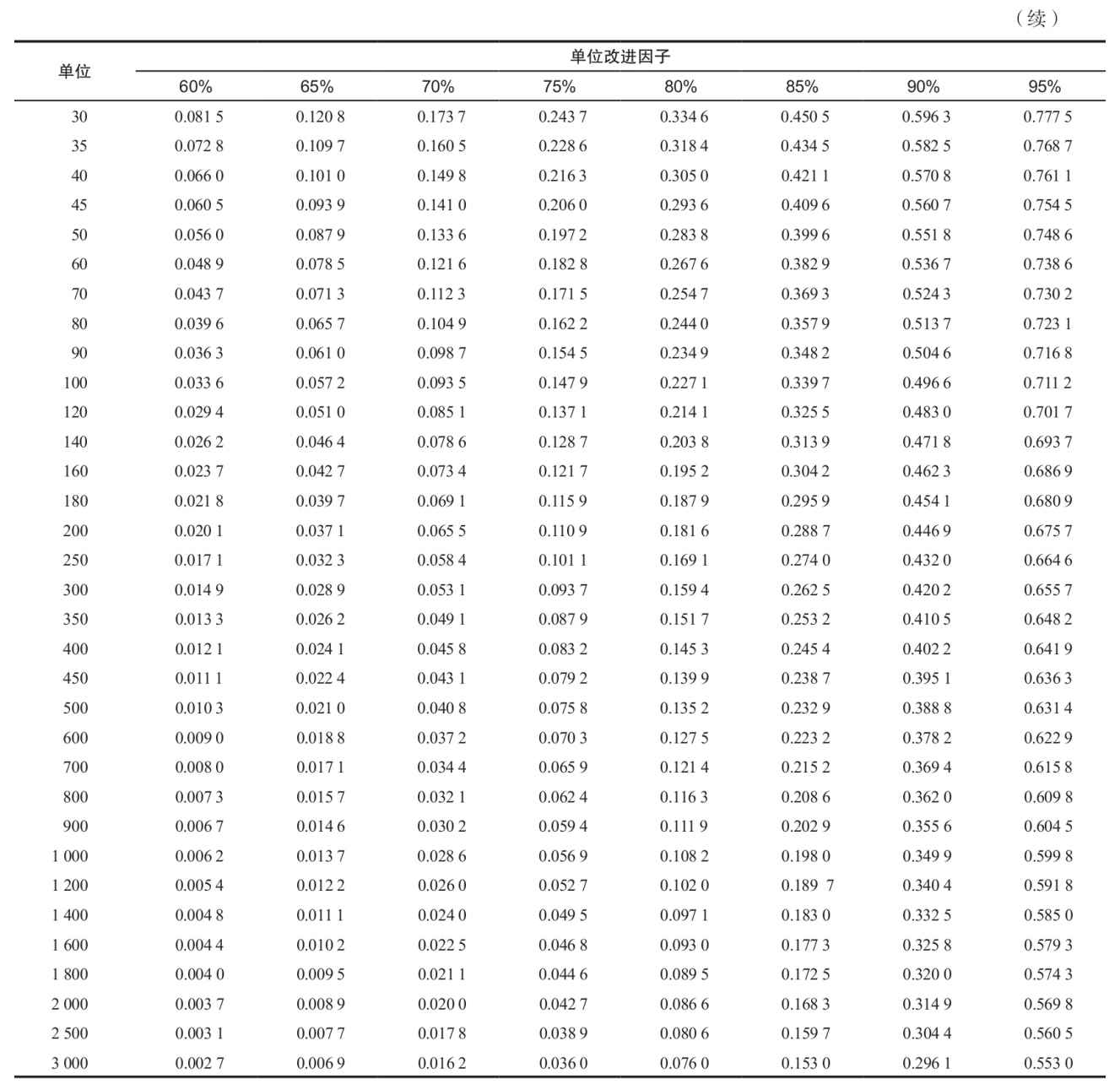
表6-3　學習曲線累計改進因子表

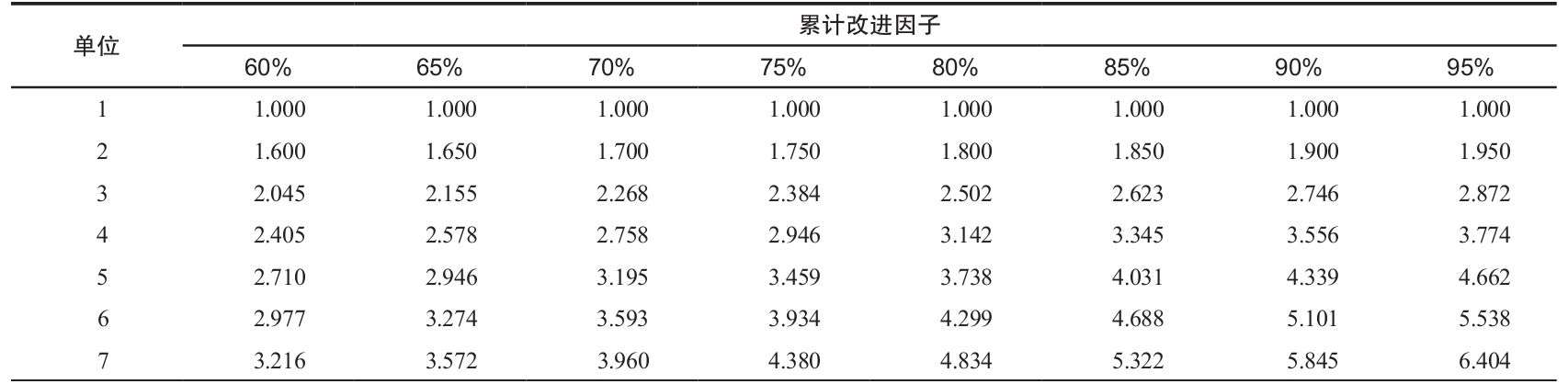
詳細解釋如下，假設我們要嚴格檢查表6-1中第16個單位產品的勞動小時數和累計勞動小時數。查表6-2可知，第16個單位產品在80%的學習率下的改進因子為0.409 6，該數乘以100 000（生產第1個單位產品的小時數）得40 960，同表6-1中的結果完全一樣。從表6-3中可知，前16個單位產品的累計改進因子為8.920，乘以100 000後得到892 000，同表6-1中得出的確切值892 014非常接近。

下面是應用學習曲線解決生產問題的一個更為詳細的例子。

例6-1　簡單學習曲線問題

薩伯特潛水艇公司（SUB）的老闆雷蒙感到非常困惑。他有一份生產12艘潛水艇的合同，並且已經生產了4艘。他發現主管生產的經理——年輕的歐裡克先生，在生產4艘潛水艇後，抽調越來越多的工人到魚雷艇裝配線上去工作了。例如，生產第1艘潛水艇需要225名工人，每人工作1周，工作時間為40小時，生產第2艘潛水艇所需要的工人少了45名。歐裡克已經告訴他們“這僅僅是個開始”，並且說生產合同中所籤的最後一艘潛水艇將只需要100名工人。

歐裡克的計劃是基於學習曲線制訂的，但他對工人人數的削減是不是做得有些過分了呢？

解答

因為生產第2艘潛水艇需要180名工人，由簡單的指數曲線可知學習率為80%（=180÷225）。為了求出生產第12艘潛水艇需要多少工人，我們在表6-2中查一下學習率為80%的第12個單位的改進因子，並將此值乘以生產第1艘潛水艇需要的工人數。改進因子為0.449 3，需要101.092 5（=0.449 3×225）名工人（注意，電子表格可用於查找表中未包括的值，它們可直接從式（6-1）中計算得到）。因此，歐裡克對生產最後一艘潛水艇所需的工人人數的估計只比真正所需工人人數少1人。

例6-2　使用學習曲線估算成本

SUB公司生產第一艘小型潛水艇的成本為500 000美元，其中200 000美元為材料成本，300 000美元為勞動成本。基於以上成本，公司可接受的利潤率為10%，且公司願意基於70%的學習率簽訂一份合同。那麼簽訂生產3艘潛水艇合同的協議價格應該是多少？

解答

如果生產受到干擾，那麼將需要重新學習。在某些情況下，可以估計出學習曲線上新的時間位置。

6.2.3　估計學習率

如果已經開始生產了一段時間，那麼通過以前的生產記錄能夠很容易地得到學習率。一般而言，生產時間越長，估計就越準確，因為生產初期可能發生很多狀況，所以大部分公司直到已生產了一些產品之後才開始收集用於學習曲線分析的數據。

如果生產還未開始，對學習率的估計就是一個具有啟發性的猜測問題。在這種情況下，分析人員可以有以下三種選擇：

（1）假設學習率與同一行業以前應用的學習率一樣。

（2）假設學習率與相同的或類似的產品的學習率是一樣的。

（3）分析目前的運營方式與之前的運營方式的相同點和不同點，並由此得出最適合此種情況的修正了的學習率。

6.2.4　學習時間應該持續多久

生產在經過一定階段後產出是否會穩定下來呢？還是對生產的改進會持續下去呢？有些領域的改進可以持續幾年甚至幾十年（如收音機、計算機和其他電子產品，如果我們考慮通貨膨脹的影響，那麼汽車、洗衣機、電冰箱和大部分製造類產品也屬於這種情況）。如果學習曲線對幾百件甚至幾千件產品都有效，那麼對以後的幾百件甚至幾千件產品還會繼續有效。從另一方面來說，高度自動化系統的學習曲線，其學習率可能近似為1，因為安裝系統之後，它們很快就達到了一個穩定的生產水平。