e1 Zvi Bodie 投資學 v10
習題
基礎題
1.長期債券的價格較短期債券波動更大。但是,短期債券的到期收益率比長期債券波動大。如何調和這兩種經驗觀察?
2.一種無限期的年金,其久期會短至10年或是20年嗎?
中級題
3.9年期債券,收益率為10%,久期是7.194年。如果市場收益率變動50個基點,債券價格變動百分比是多少?
4.某債券的剩餘期限是3年,到期收益率為6%,每年付息一次,票面利率是6%,其久期是多少?如果到期收益率變為10%,久期又是多少?
5.如果第4題中的利息每半年支付一次,債券的久期是多少?
6.2008年金融危機期間,AAA級債券和國債之間的歷史利差大幅度擴大。如果你相信利差將會迴歸到歷史正常水平,你將會採取什麼行動?這是哪種形式的債券互換?
7.你預測利率即將下跌。哪種債券將會為你帶來最高的資本利得?
a.低票面利率,長期限。
b.高票面利率,短期限。
c.高票面利率,長期限。
d.零息,長期限。
8.給下列兩組債券的久期或有效久期排序。
a.債券A的票面利率為6%,20年期,以面值出售。債券B票面利率是6%,20年期,以低於面值的價格出售。
b.債券A是20年期的票面利率為6%的不可贖回附息債券,以面值出售。債券B是20年期的票面利率為7%的可贖回附息債券,以面值出售。
9.一家保險公司必須在1年內向客戶支付1000萬美元,並在5年內支付400萬美元。收益率曲線在10%時是平的。
a.如果公司想通過單一的一種零息債券來充分融資以免疫對該客戶的債務,則它購買的債券的期限應為多久?
b.該零息債券的面值和市場價值各是多少?
10.長期國債當前出售的到期收益率接近6%。你預計利率會下降,市場上的其他人認為在未來一年內利率會保持不變。假定你是正確的,對以下每種情況,選擇能帶來較高持有期收益的債券。簡述理由。
a.ⅰ.Baa級債券,票面利率為6%,到期期限20年。
ⅱ.Aaa級債券,票面利率6%,到期期限20年。
b.ⅰ.A級債券,票面利率3%,剩餘期限20年,105時可贖回。
ⅱ.A級債券,票面利率6%,剩餘期限20年,105時可贖回。
c.ⅰ.票面利率為4%的不可贖回國債,20年期限,到期收益率為6%。
ⅱ.票面利率為7%的不可贖回國債,20年期限,到期收益率為6%。
11.當前,期限結構如下:1年期債券收益率為7%,2年期債券收益率為8%,3年期債券和更長期限債券的收益率都是9%。你正在1年期、2年期和3年期債券中做選擇,所有債券均是每年一次支付8%的利息。如果你確信年底時收益率曲線會在9%處持平,你將購買哪種債券?
12.在未來兩年底,你要支付10000美元的學費,且債券當期的收益率為8%。
a.債務的現值和久期各是多少?
b.什麼樣期限的零息債券可以使你的債務免疫?
c.假設你購買一種零息債券,其價值和久期與你的債務相同。現在假設利率立即上升至9%。你的淨頭寸將會發生什麼變化?換句話說,你的學費債務和債券價值之間的差異會有什麼變化?如果利率降低7%,又會如何?
13.養老金向受益人支付終身年金。如果一家公司永久地參與這項業務,養老金債務則類似於終身年金。因此假定,你來管理這一年金,每年向受益人支付2億美元,永不終止。所有債券的到期收益率都是16%。
a.如果5年期票面利率為12%(每年支付)的債券的久期是4年,而且20年期且票面利率為6%(每年支付)的債券久期是11年。要使你的債務完全融資並免疫,則每種債券持有量為多少?(以市價計算。)
b.你持有的20年期附息債券的面值是多少?
14.你正在管理100萬美元的資產組合。你的目標久期是10年,你可以從以下兩種債券中選擇:5年期的零息債券和終身年金,當期收益率均為5%。
a.在你的資產組合中,你將持有兩種債券各多少?
b.如果你現在的目標久期是9年,明年持有比例會發生什麼變化?
15.我的養老基金計劃將在10年期間每年支付給我10000美元。第一筆支付將在5年後。養老基金想將其頭寸免疫。
a.養老基金對於我的債務的久期是多少?當期利率為每年10%。
b.如果養老基金計劃使用5年和20年零息債券來構建免疫頭寸,每隻債券要投入多少資金?每隻零息債券的面值是多少?
16.30年期的債券,每年支付一次,票面利率為12%,久期是11.54年,凸性為192.4。該債券在8%的到期收益率水平出售。如果債券的到期收益率下跌至7%或上漲至9%,使用財務計算器或電子數據表計算債券價格。按照新的收益率,根據久期法則和凸性久期法則,債券價格是多少?每種方法的誤差百分比是多少?對於這兩種方法的準確性,你有何結論?
17.特許金融分析師梅耶斯是一位大型養老金的固定收益投資經理。投資委員會的成員斯派西對學習固定收益組合管理非常感興趣。斯派西向梅耶斯提出了幾個問題,尤其是斯派西非常想知道的固定收益投資經理如何配置投資組合,以從對未來利率的預期中獲利。
梅耶斯使用一隻固定利率債券和票據向斯派西說明固定收益交易策略。兩隻債券都是半年的付息期。除非特別說明,所有的利率變化都是同步的。兩種證券的特徵如表16-9所示。他還考慮一隻9年期的浮動利率債券,每半年支付一次浮動利率,當前的收益率是5%。
表16-9 固定利率債券和固定利率票據的特徵
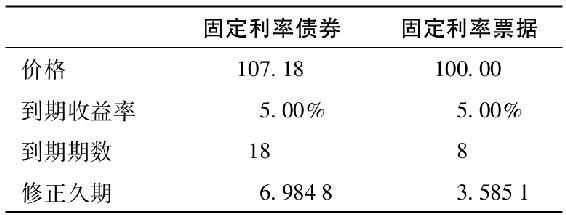
斯派西問梅耶斯當預期利率上升時,固定收益投資經理如何進行資產配置。以下哪種是最合適的策略?
a.降低組合的久期。
b.買入固定利率債券。
c.拉長組合的久期。
18.斯派西讓梅耶斯(見上題)從利率變化中確定價格變化量。為了說明,梅耶斯計算了表中固定利率票據的價值變化。特別地,他假定利率水平上升了100個基點。運用表16-9中的信息,預計固定利率票據的價格變化是多少?
19.某30年期限的債券,票面利率為7%,每年付息一次。今天的出售價格為867.42美元。某20年期限的債券,票面利率是6.5%,也是每年付息一次。今天的出售價格是879.50美元。債券市場分析師預測5年後,25年期債券將以到期收益率8%的價格出售,而且15年期債券將以到期收益率7.5%的價格出售。因為收益率曲線向上傾斜,分析師認為利息將投資於利率為6%的短期證券。5年後哪一種債券可以提供較高的期望收益率?
20.a.如果年利率上升至12%,運用數據表計算表16-3中兩隻債券的久期。為什麼附息債券的久期下降而零息債券的久期不變?(提示:考察F欄中計算的權重發生了什麼變化。)
b.如果票面利率是12%而不是8%,且半年的利率還是5%,使用同樣的電子數據表計算附息債券的久期。解釋為什麼久期比表16-3中的久期低(再次查看F欄。)
21.a.構建一張電子數據表計算5年期,票面利率8%,每年支付一次,初始到期收益率為10%的債券的凸性。
b.5年期零息債券的凸性是多少?
高級題
22.某零息債券的期限是12.75年,在到期收益率8%的水平出售(有效年收益率),凸性為150.3,修正久期為11.81年。30年期,票面利率為6%,每年付息一次的附息債券同樣在到期收益率為8%的水平賣出,與零息債券的久期相同——11.79年,但是凸性顯著高於零息債券,為231.2。
a.假設兩種債券的到期收益率都上升至9%。每種債券資本損失的百分比是多少?根據久期凸性法則預測出來的資本損失百分比是多少?
b.重複問題a,但此次假設到期收益率下降至7%。
c.比較兩種場景下兩隻債券的表現:一種是利率上升,一種是利率下降。根據不同投資表現,解釋久期的吸引力。
d.根據你對問題c的回答,如同此例,如果兩種債券的收益率等量上升或下降,你認為有可能使兩種久期相同而凸性不同的債券在初始時以同樣的到期收益率來定價嗎?在這種情況下,有人願意購買較小凸性的債券嗎?
23.新發行的10年期債券,票面利率為7%(每年付息一次),債券以面值出售。
a.債券的久期和凸性是多少?計算凸性。
b.假設到期收益率即刻從7%上漲至8%(期限仍然是10年),計算債券的實際價格。
c.根據式(16-3)得到的價格是多少?公式的誤差百分比有多大?
d.根據式(16-5)得到的價格是多少?公式的誤差百分比有多大?
24.a.使用電子表格來回答如下問題,假設收益率曲線維持在4%的水平。計算出一個“子彈頭”式固定收益投資組合的凸性(即一筆單一現金流構成的投資組合,該筆現金流在5年後收回)。
b.現在,計算出一個“槓鈴”型固定收益投資組合的凸性,即在一段時間內使用相等的現金流進行的投資組合。假設證券在第1~9年每年產生100美元現金流,使得它的久期接近a中的子彈型。
c.是“槓鈴型”還是“子彈型”擁有更大的凸性?