e3 Harold Kerzner 項目管理 v12

17.4　確定性、風險及不確定性

決策過程可歸結為 3個範疇：確定性、風險及不確定性。（決策過程與定量風險分析相關，包括收益矩陣、期望值和決策樹，但不限於此，見17.10節中的分析。）確定狀態下的決策過程是最容易的事情。在確定狀態下，我們假定很容易獲得所有必需的信息去做正確的決策，而且我們對結果很有信心。

17.4.1　確定狀態下的決策

所謂確定狀態下的決策，意味著我們能百分之百地瞭解事件的性態（state of nature）以及每種性態的結果。從數學上看，這可以通過支付矩陣來表達。要建立一個支付矩陣，必須先識別（或選擇）我們所不能控制的事物的性態，然後選擇針對不同性態所能採取的行動，這通常被稱為策略。該矩陣中的要素就是每個策略的成果。基於確定性狀態下進行決策所建立的決策模型具有兩個主要特徵：

• 無論事物以何種性態出現，我們都能獲得一種主要的、具有支配作用的策略。該策略比其他任何策略收入更高，損失更小，並適用於事物的所有性態。

• 在事物的各種性態之間沒有發生概率的分佈機制（每一種性態具有相同的發生概率）。

例

某公司欲投資5 000萬美元開發某類新產品。該公司將市場性態分為3類：N 1 代表較強的市場需求，N 2 代表中等狀況的市場需求，N 3 代表較差的市場需求。該公司還提出 3種戰略，即S 1 、S 2 、S 3 ，分別以A、B、C表示。（本例中還有所謂的S 4 戰略，即不開發此項產品，既無收益又無損失，我們在此將其省略。）假定這個決策是基於開發產品的考慮。我們用支付矩陣將其表示出來，如表17-2所示，S 3 戰略在任何市場性態下都是盈利最多的戰略，從而在開發新產品時也就成為該公司的首選戰略。

圖17-2　支付矩陣　　　　　　　　　　 　　單位：100萬美元

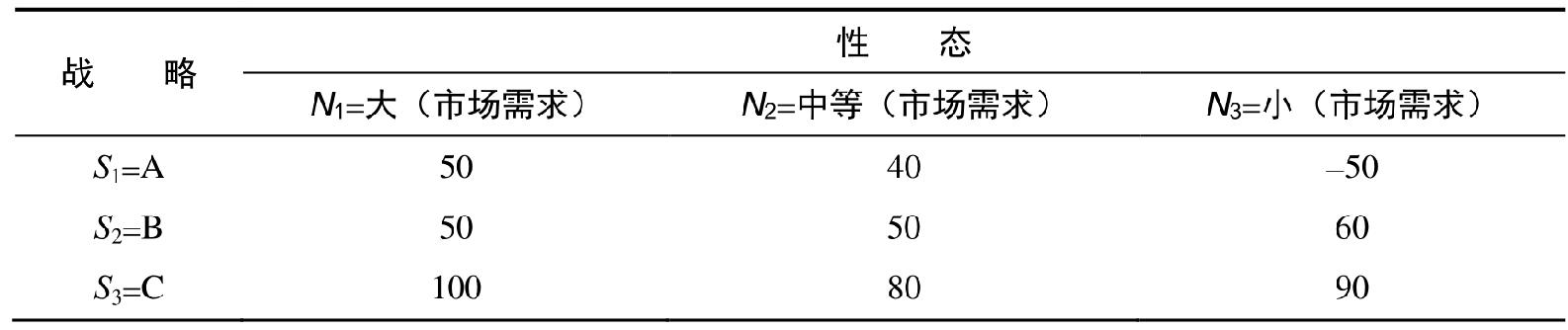
17.4.2　風險狀態下的決策

大多數的事件中，並不存在適用於全部形態的主要戰略。在現實世界中，常常是高利潤伴隨著高風險和高損失。如果不存在某一主要戰略，就必須考慮各種性態的發生概率。風險可以被視為某一確信限度（如概率分佈）的結果（如各種性態）。事件的概率分佈常常可以通過嚴謹的實驗數據來估計或定義。考慮表 17-3，此矩陣僅僅將表 17-2支付矩陣中狀態N 3 下的戰略S 1 ~S 3 的收益值相互交換了。

表17-2也可用下標符號來表示：以Pi , j 代表表中的要素，P 為收益，i 為橫軸（戰略），j 為縱軸（性態）。例如，P 2,3 就表示在需求較小的市場性態（N 3 ）下采用戰略S 2 所產生的收益。需要注意的是，採用此方法時，矩陣並不一定是正方形的，但至少是矩形的（事物性態的類型有可能不等於戰略的數目）。

圖17-3　收益表　　　　　 　　單位：100萬美元

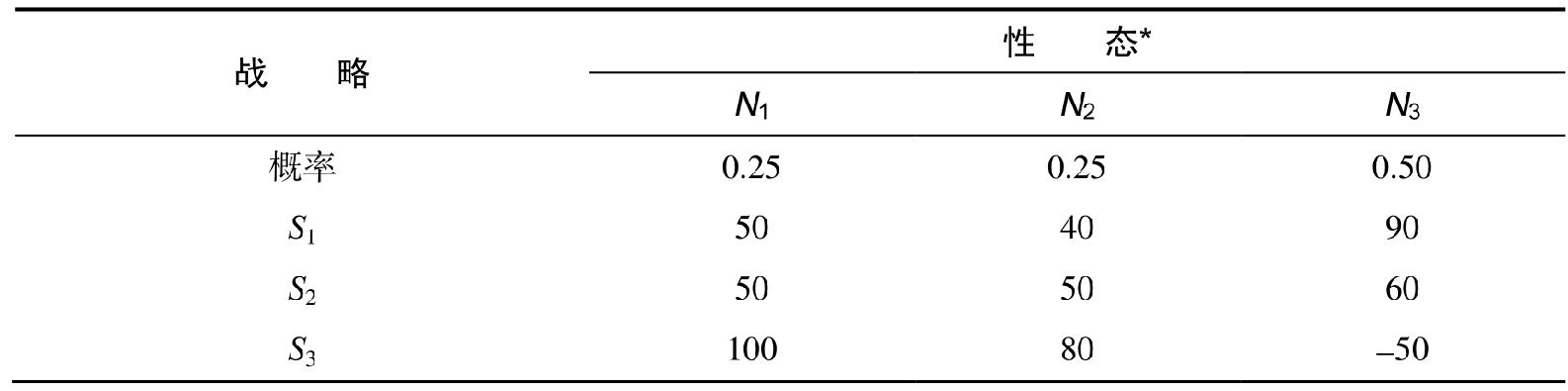
注：* 數字代表每一性態的發生概率。

從表17-3中可以看出，這裡沒有支配性的主要戰略，所以需要考慮各種市場性態的發生概率。最佳的選擇是期望值最高的戰略，期望值是每一種戰略在每一種市場性態下的收益乘以該性態發生的概率，並加總求和的結果。期望值用數學公式表達為：

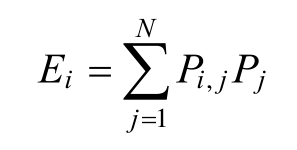
式中　Ei 　——戰略i 的期望值；

Pi ， j ——結果要素；

Pj 　——每種性態發生的概率。

例如，S 1 戰略的總期望值為：

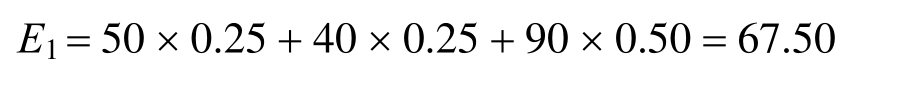
同理可得，E 2 =55，E 3 =20。在期望值計算的基礎上，企業會選擇S 1 戰略。如果兩種戰略所產生的期望值相等，我們就可以參照其他要素（如發生頻率、資源可用性、影響時間等）進行選擇。（注意：只有在風險中立者的效用關係基礎上，才能進行期望值計算。如果決策者不是風險中立者，那麼這類計算不一定有效，產生的結果將視其風險容忍度的差別而有所不同。）

為量化任何一種潛在後果，我們必須確認將要採用的戰略、期望收益以及該種性態發生的概率。本例中，我們選用S 1 戰略，就是因為其最後期望收益最高（其他條件保持不變）。一般來講，人們只考慮期望收益為正數的風險；若期望收益為負數，則該風險極有可能是我們應預先防範的風險。

在這種決策中，一個重要因素是各種性態的發生概率問題。概率設定是否正確會影響到計算的結果以及最終的戰略抉擇。在表17-3中，若我們將三種市場性態概率改為0.6、0.2、0.2，期望收益就會分別變成 E 1 =56、E 2 =52、E 3 =66。在該狀態下，企業會選擇 S 3 戰略（其他條件保持不變）。

17.4.3　在非確定性狀態下進行決策

風險與不確定性（非確定性）之間的區別在於，風險狀態中，各種性態的發生有一定概率；而在不確定性狀態中，各種性態的發生概率無法得知。不過和風險決策一樣，不確定性決策也常常意味著不存在某種支配性戰略。通常，決策者可提出4套準則來進行決策，採用哪套準則取決於項目的類型以及決策者的風險容忍限度。

第一套準則稱為哈維茨法（該方法由諾貝爾經濟學獎獲得者 Hurwicz提出），也稱極大極大準則。如果用此準則，則決策者是樂觀主義者，其採用何種戰略完全以戰略所產生的最大收益為準。例如，表17-3中最大收益100為S 3 所產生，則決策者為追求100的收益而選擇S 3 戰略；但S 3 戰略在N 3 性態下的損失也是最大的，因此選擇這種戰略還必須有足夠的財力承擔可能的風險或損失。實力雄厚的大企業會採用這種方式，中小企業則對可能損失最小為準則的方法較有興趣。

第二套準則是小企業常用的懷爾德法（Wald），也稱極小極大法則，決策者在此多半隻注意他能承擔多大的損失。該法比較保守，試圖降低最大可能的損失。

在哈維茨法中，我們只考慮了表17-3中每種戰略的最大收益；而在懷爾德法中，我們僅考慮最小收益。在該表中，S 1 、S 2 、S 3 三種策略的最低收益分別為 40、50、−50，企業為縮小最大可能損失而選擇S 2 戰略。如果三個方案的收益都是負數，項目經理會選擇損失相對最小的方案。但如果考慮不同企業的財力，也有可能任何一種都不選。

第三套準則稱為塞維格法（Savage），也稱極大極小法。假設決策者對損失的痛苦異常敏感，他會盡力降低選擇的最大後悔度。

採用此法的第一步是從最大值中扣除每一列的所有值，做一張“後悔值”表格。把這種方法用於表17-3，就可以得到表17-4。

圖17-4　後悔值表

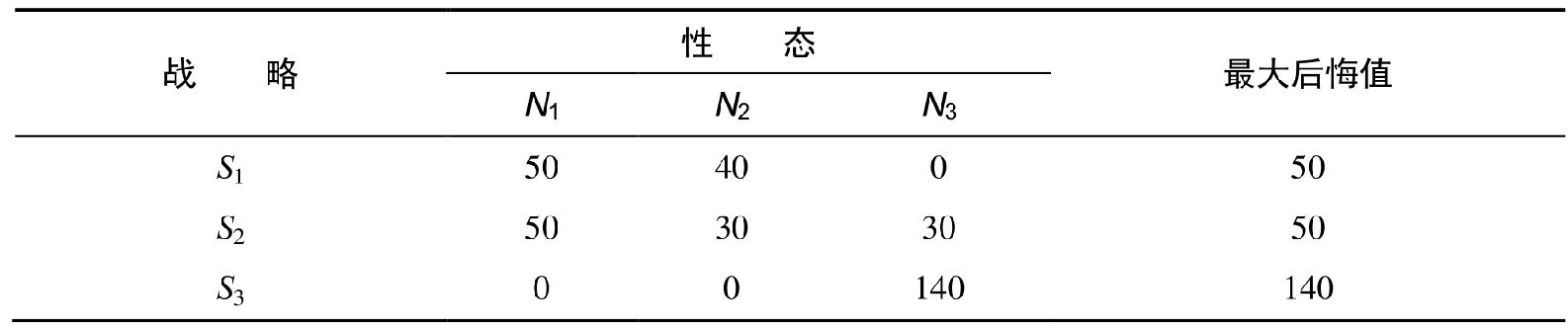
每一結果元素的後悔值可通過從該列最大值中扣除該結果元素而得出。每行的後悔值的最大值即該戰略的最大後悔值。換言之，如果決策者選擇戰略S 1 或S 2 的最大後悔值均為50，而選擇戰略S 3 的最大後悔值為140，則決策者會選S 1 或S 2 。

第四套準則稱為拉普拉斯準則（Laplace），也叫等可能性準則。這種方法實際上是努力將不確定性決策轉化為風險決策。風險與不確定性之間最大的區別是性態發生概率的確定。拉普拉斯法在貝葉斯（Bayesian）統計原理的基礎上，假定各種性態發生概率全部相等，於是不確定性決策轉化為風險決策，接著可按風險決策方法進行決策，即選擇期望收益最大的戰略。在表17-3中應用拉普拉斯法則，即假設P 1 =P 2 =P 3 =1/3，便得到表17-5。決策者根據拉普拉斯法則將選擇S 1 戰略。

圖17-5　拉普拉斯法則

所有的不確定性決策最後都會歸結為一點，即盡力將不確定性轉化為項目管理者可以管理的風險。關於這四種準則，戰略的選擇主要取決於企業的資金能力及風險容忍限度。

17.4.4　在非確定性狀態下進行決策

期望值可以與概率及決策樹結合在一起來識別和量化潛在風險。另一個方法是製作影響分析表。決策樹法適用於決策過程較為分散、不成一體的情況。在該情況下，決策者同時分析幾種決策。（此處仍假設是風險中立者。）

圖17-3介紹了決策樹。圖中各條分支末端（最右端）的概率由各條分支的概率相乘而得出。

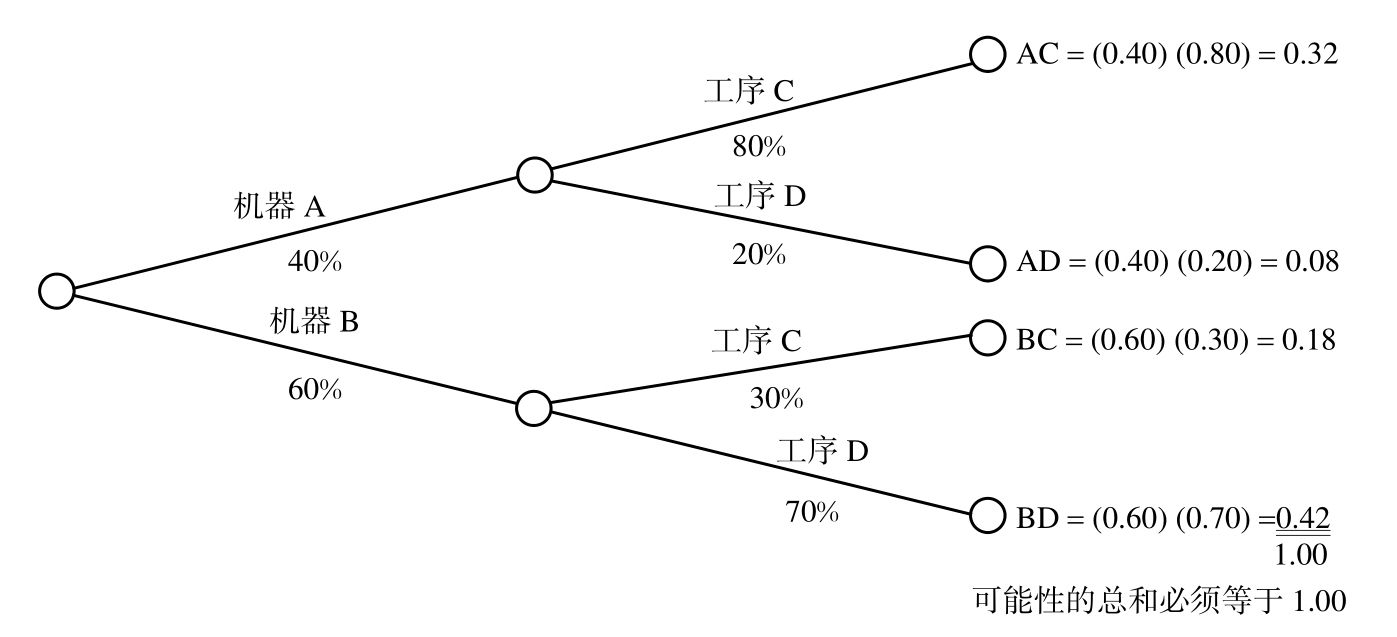
圖17-3　決策樹

對於更復雜的問題，決策樹的制定過程就更加複雜了。決策樹包含兩個要素：一是決策點，通常用方框表示，該點表示決策者必須做出某種選擇；二是機會點，用圓圈表示，通常表示有機會存在。［決策樹方法的關鍵假設是風險中立（見17.2節）。決策樹中期望值的計算不是平均結果，是一種風險中立的結果。］

建立決策樹有如下幾個必要的步驟：

• 建立一棵邏輯樹，通常從左至右，包括決策點和機會點。

• 將事物各種性態的發生概率標示在“樹”上。

• 計算出各種方案的收益，然後完成決策樹。

考慮下面的問題。某產品可以自制，也可以外購。若自己做，需付3.5萬美元買新設備，若市場狀況好（概率為0.70），收益為8萬美元；若市場狀況較差（概率為0.30），只有3萬美元收益，不包括設備成本。如果將工作外包出去，那麼合同管理費用為5 000美元。若市場好可盈利5萬美元，若市場差則只賺1.5萬美元。圖17-4說明了該問題的決策樹。在這個問題中，外包戰略比自制戰略收益的期望值大4 500美元。因此，我們應該選擇外包戰略。

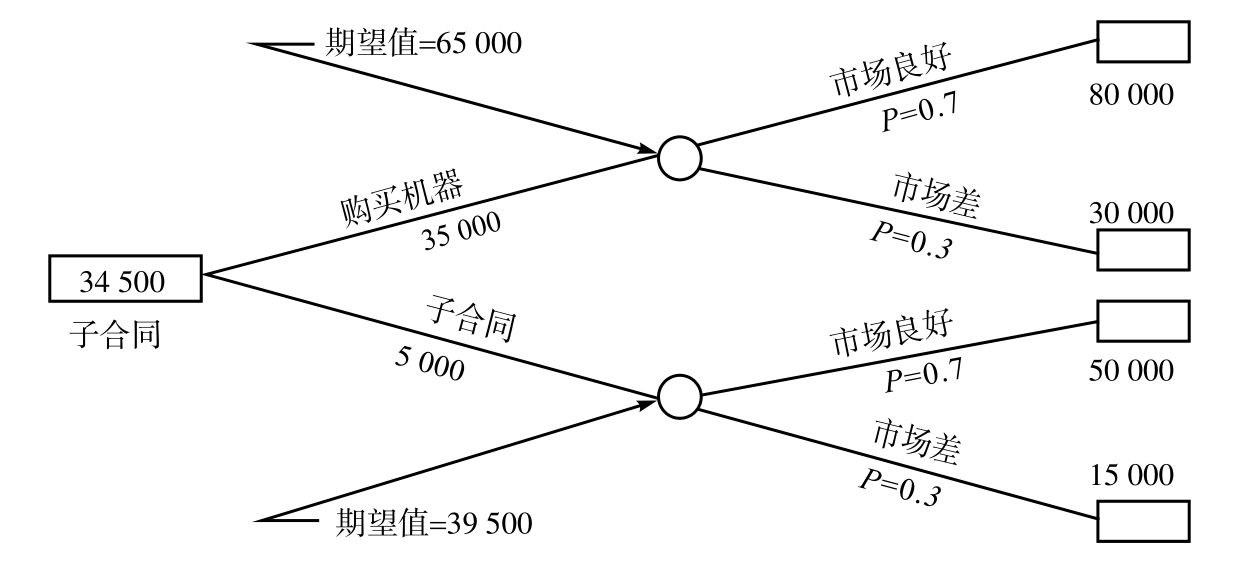
圖17-4　擴展決策樹（單位：美元）