e2 Sanjeev Bordoloi 服務管理：運作、戰略與信息技術 v9
16.6.3 對項目完成時間分析的評價
我們對於項目完成時間分佈的分析是基於一個關鍵假設，即通過期望活動時間計算出的關鍵路線是真正的關鍵路線。這個假設之所以非常重要，是因為它假定在所有不確定活動完成之前我們就已經知道了這條關鍵路線。而實際上，關鍵路線本身也是一個隨機變量，在項目完成之前它也是不確定的。我們知道，關鍵路線的時間是不確定的，且呈概率分佈，同樣，其他路線的時間也是不確定的。因此，可能有一條預期時間比關鍵路線短的路線最後卻成了關鍵路線，因為這條路線上的活動用的時間比預期要長得多，最終結果是未認定為關鍵路線的路線決定了項目的完成時間。所以，當我們只考慮一條關鍵路線時，對項目完成時間期望和方差的估計就發生了偏差。從方差角度看，它也許偏高也許偏低，但是，項目期望完成時間總是偏於樂觀的。因為，真正的期望完成時間總是大於或等於我們所估計的時間。
一個簡單的原則可以幫助我們理解這些估計的準確性：如果關鍵路線的期望時間比其他路線的期望時間長得多，這種估計可能就是正確的。在這種情況下，關鍵路線非常可能決定項目的完成時間。然而，如果一個項目網絡中包含一些總的緩衝時間很少的非關鍵路線，那麼，這些活動就可能影響項目完成時間。這種情況稱作“合併節點偏差”（merge node bias）。也就是說，項目的結束節點有很多路線在那裡聚合，其中每一條都有可能成為確定項目完成時間的關鍵路線。在我們的分析中，只有最可能的路線被假設為關鍵路線，所以，我們估計的項目完成時間分佈就可能偏於樂觀，因為其他接近關鍵的路線都被忽略了。例16-6就表明，當一個準關鍵路線包含一項有很大方差的活動時，它對於完成項目的概率會有影響。
⊙【例16-6】
網球比賽——合併節點偏差
項目進行了幾天，我們發現購買網球和獎品（即活動G）所花費的時間可能比預想的要多一些，所以，我們修改估計為A=2、M=3和B=28，這對在24天內完成項目的可能性有什麼影響呢？
首先，我們利用式（16-8）和式（16-10）重新計算活動G的期望時間和方差，得出t=7，σ2=676/36，回想圖16-7中，活動G最初有4天期望時間，並有4天緩衝時間，所以我們把期望時間修訂為7天，活動G仍然是非關鍵性的且TS=1。然而，因為活動G的方差很大，所以它有可能使A-C-D-G-I-J成為一條關鍵路線。這條準關鍵路線的完成時間分佈可以用以下方式來確定：
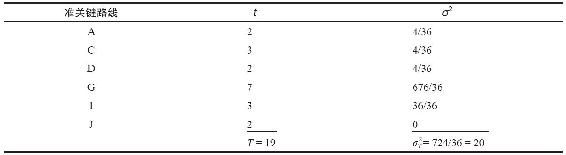
現在我們可以利用這條準關鍵路線的T和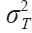
確定在24天內完成項目的概率了。標準差Z的值，可用式（16-11）來計算：
利用Z=1.12查標準正態分佈表，我們可以知道在24天內完成項目的概率為0.87，這條準關鍵路線的完成時間分佈如圖16-16所示。所以，一個含有大方差活動的準關鍵路線是不能被忽略的，因為事實上，這樣的路線可能會變成關鍵路線並延誤工期，計算機仿真（見第13章附錄）是更準確地確定項目完成時間分佈的一種方法。
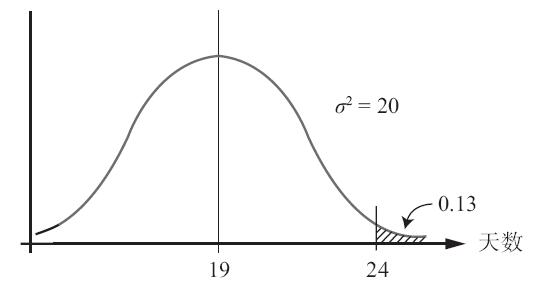
圖16-16 準關鍵路線完成時間分佈