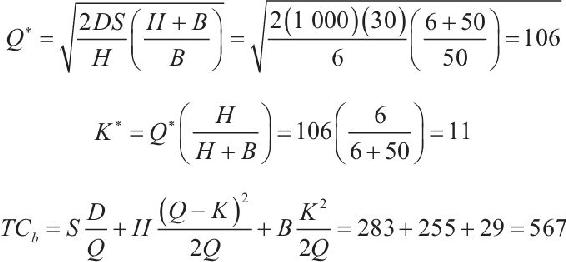e2 Sanjeev Bordoloi 服務管理：運作、戰略與信息技術 v9

15.3.3　考慮有計劃的短缺時的庫存模型

當顧客願意容忍庫存短缺時，可以應用計劃短缺庫存模型。例如，一家輪胎商店可能沒有預備各種尺寸的高性能輪胎，因為該商店瞭解：當某一特殊型號的輪胎缺貨時，顧客願意等一兩天。但是，為使顧客接受這一戰略，商店必須信守所許諾的到貨時間，而且這一時間的長度必須合理。否則，顧客將會覺得該商店不可靠而轉投其他商店。

電子數據交換（EDI）和供應商交貨時間的可預測性保證了最少庫存戰略的實施，這一系統的收益取決於庫存維持成本和可延遲訂貨的缺貨成本之間的權衡。如果顧客願意去等待一件目前暫時缺貨的商品，則銷售就沒有喪失，但是應當考慮一下給顧客造成不便的一些主觀成本損失。軟件製造商通過創造“霧件”（vaporware，即已計劃生產但仍未實際獲得的軟件）來極大化對缺貨的容忍度。這種公司通過廣告宣傳這些霧件來估計該產品的需求水平，然而，如果這一戰略實施過多，就會影響公司在顧客心目中的信用形象。對零售商來說，這一戰略對顧客的吸引力在於庫存成本的節省使商品價格降低。

圖15-7描述了有計劃短缺庫存系統的理想行為，該圖基於如下假設：①需求率為常數；②顧客將願意等待，直到下一批訂貨量Q到達，補充已積累到最大值K的缺貨量。在以上兩點假設下，稱為“允許缺貨時的總成本”（TC_b）的新的總庫存成本公式如下：

式中　K——當訂貨到達時已短缺的庫存數量；

B——以美元表示的每年每單位缺貨成本。

引入幾何中相似三角形的比例關係理論（例如，直角三角形中邊和高互成比例），注意到真實的庫存只佔整個庫存週期的一小部分，則平均庫存的表達式可由下導出：

由相似三角形知：T₁/T=(Q-K)/Q。代入上式，得：(Q-K)²/2Q。

同理，可得平均延遲庫存的表達式為：

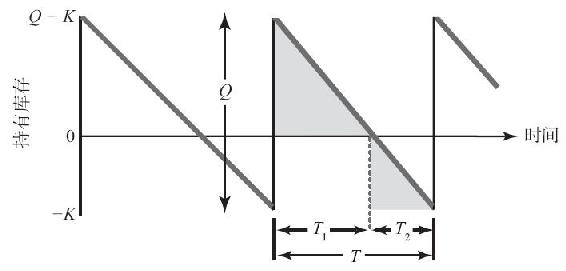
圖15-7　有計劃短缺模型中的庫存水平

由相似三角形知：T₂/T=K/Q。代入上式，得：K²/2Q。

由於式（15-5）總庫存成本中含有兩個待定變量Q和K，所以對訂貨量和延遲訂貨量進行微分，解出每一個變量值：²

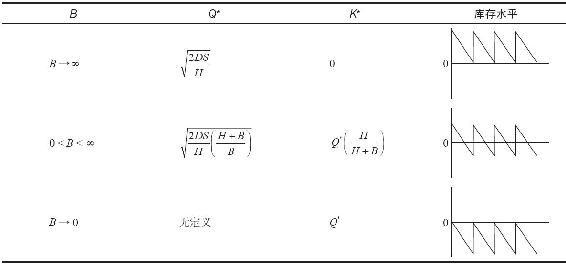
如表15-3所示，當延遲訂貨成本B允許在（0，∞）內取值時，計劃短缺系統以及式（15-6）、式（15-7）都會帶給我們有關庫存系統的大量信息。如表15-3所示，用∞代替式（15-6）中的B，則得到傳統的EOQ式（15-3）。這樣，當傳統EOQ公式應用於企業時，則暗含延遲訂貨成本無窮大，因此庫存短缺不會發生。但延遲訂貨成本實際上是一個有限值，因此應用EOQ公式會導致存貨系統成本不恰當的上升。

若延遲訂貨成本為零，則EOQ值無定義（因為零被當作除數），但這種情況下的庫存模型的確存在。例如，病人在等待心臟移植，因為捐贈者是不能被貯存的，所以等待接受捐贈的病人就處於延遲訂貨狀態。

表15-3　作為延遲訂貨成本功能的Q^*和K^*值

⊙【例15-3】

落基山電力公司——有計劃短缺問題

假設玻璃絕緣體延遲訂貨的成本是付給聯邦快遞公司的50美元滯留費。代入式（15-6）和式（15-7），計算一個新的訂貨量和最大的延遲訂貨積累量。和傳統的EOQ方法相比，有沒有年總成本節餘呢？

在EOQ=100時，TC_p=600美元，比上面計算得到的TC_b多33美元。因此，用簡單的EOQ模型，成本會增加，因為它假設庫存短缺不會發生。注意，當以年為單位來計量時，訂貨和維持成本都大幅度下降到300美元以下，因為這一EOQ模型中延遲訂貨成本僅為29美元。