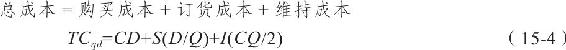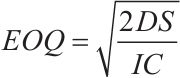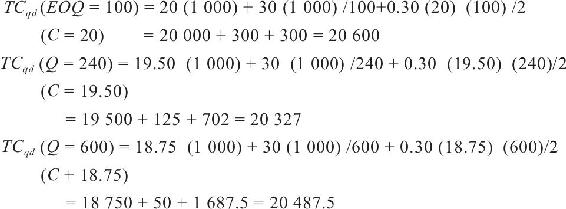e2 Sanjeev Bordoloi 服務管理：運作、戰略與信息技術 v9

15.3.2　考慮數量折扣時的庫存模型

供應商也有感興趣的訂購量，由於啟動生產耗費金錢，故有自己的經濟批量規模。例如，準備四打巧克力餅乾的花費和努力與準備一打的花費相差甚微。同樣的道理，生產廠商也會鼓勵顧客每次多買以減少自己的成本；而且，一整卡車貨物的運費比半卡車貨物的運費均攤起來要少得多。因此，對大批量訂貨的顧客給予價格或數量上的折扣是互惠互利的。通常，只有訂購比EOQ多得多的貨物量時，才會有可觀的價格折扣。因此，需要在節省的購買成本與維持過量庫存的費用之間加以權衡。為了研究該權衡問題，我們要將貨物的價格看作一個變量，將它包括在年總成本當中。加入購買成本，式（15-2）則變為“數量折扣總成本”（TC_qd）的新公式：

式中　C——貨物的單位成本（用美元表示）；

I——以貨物成本的百分比表示（以小數表示）的年庫存維持成本（注意：IC=H）。

為了證明數量折扣情況下給出的權衡分析模型，我們再回頭看落基山電力公司的例子。

⊙【例15-2】

落基山電力公司——數量折扣問題

玻璃絕緣體SKU1341的供應商正與RMP談判，試圖讓其訂購比100片SKU1341多得多的批量，且它給出了下列數量折扣：

RMP該如何作答呢？由於訂購數量不同，價格也不一樣，所以恰當的庫存成本模型應為式（15-4），維持成本的百分數值由IC=H得出，解得I=H/C=6/20=30%=0.30。然而，當考慮到購買成本、訂貨成本和維持成本時，如何應用式（15-4）去計算每年總庫存成本最小時的訂購量？一種求解方法如圖15-6所示，將總成本看作訂購量的函數，並求該非連續曲線的最低點（此例中，大量訂貨折扣價下對應的Q值為240片）。

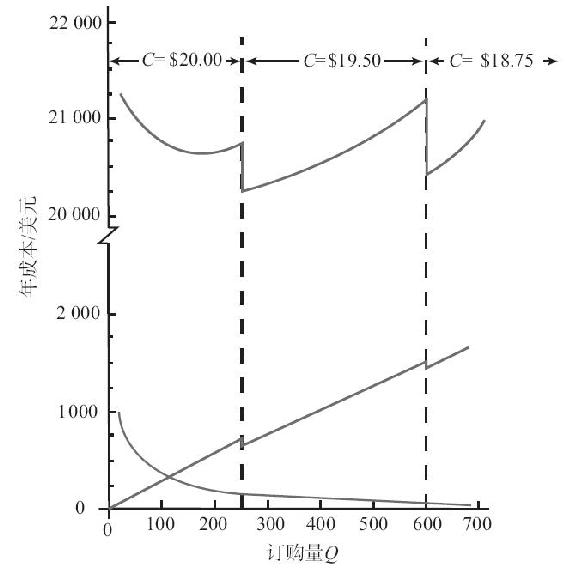
圖15-6　數量折扣模型的年成本

應用下列分析步驟也可得到相同的結論：

（1）在單位最低價處計算EOQ值，將IC=H代入式（15-3）：

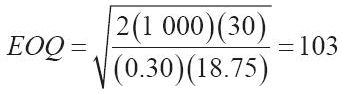，但18.75美元的價格僅適用於EOQ≥600時。

（2）假如EOQ位於正確的價格範圍之外（就如最後一段所示的那樣），則對於下一個最低價，我們要重新計算EOQ值，直到EOQ位於正確的價格範圍之內。因此，當價格為19.50美元時（將19.50代入成本C），重新計算得到的EOQ為101。然而此結果是無效的，因為在批量為240～599之間時，價格才為19.50美元。接著，我們再計算C=20美元時EOQ的值，得到100，此值正確，因為100在單價為20美元時的範圍1～239之內。下表總結了得到正確的EOQ值的一系列計算過程：

（3）將步驟2得到的EOQ值代入式（15-4），計算TC_qd，並和得到所有較高折扣價的Q值所計算出的TC_qd（TC_qd方程中的間斷點見圖15-6）比較，然後選擇使TC_qd最少的Q值：

可以看出，當訂購量為240時，年總成本最少。