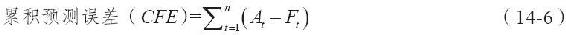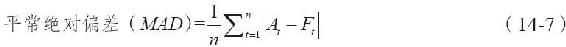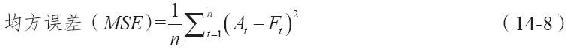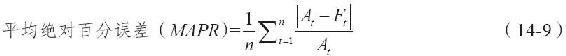e2 Sanjeev Bordoloi 服務管理：運作、戰略與信息技術 v9

14.5.3　預測誤差

雖然從圖14-1中我們可以明顯發現平滑曲線已經修勻了實際曲線的最高點和最低點，但是怎樣才能測量預測的精確度呢？

首先，我們應該期望得到一個公正的預測，可以反映實際數據的真實情況。因而，考慮到正、負的不同影響，預測誤差的總和應趨於0。如果不是這樣，接下來我們應該找出潛在的趨勢或週期性規律，並解釋說明原因。根據表14-3所示的結果，用式（14-6）計算得到的累計預測誤差（cumulative forecast error，CFE）是31。

最常見的預測誤差的方法就是使用式（14-7）計算的平均絕對偏差（mean absolute deviation，MAD）。在表14-3中，平均絕對偏差是6.6。我們將繼續使用MAD對每一個誤差進行等權平均，作為本章其餘數據預測誤差的測算結果。

如果誤差較大且非常明顯，這就需要通過調整權重來修正誤差。表14-3中計算的結果，就是通過式（14-8）計算得到的均方誤差（mean squared error，MSE），得到的修正後結果是76.6，它反映了時期5和時期6的誤差較大。

當需要對誤差進行剖析的時候，就需使用平均絕對百分誤差（mean absolute percentage error，MAPE）。例如，很顯然，10個裡面有2個誤差就比1000個裡面有2個誤差影響要大。利用式（14-9），表14-3中數據的平均絕對百分誤差就是6.8。

本例中的預測值是在α=0.5時計算出來的，此方法類似於三時期移動平均法。在前面講到的三時期移動平均法中，MAD=9.7。本例中，簡單指數平滑法預測的結果比相應的三時期移動平均法更為精確。若α=0.1，則MAD=8.8，說明小的平滑常數的不敏感性。對一組數據選取α值使MAD值最小，可以用Excel Solver表格完成。

CFE正數值31說明現存的數據有向上的趨勢，簡單指數平滑法預測降低了實際的入住率。因此，我們必須在預測中考慮趨勢調整。但是首先，我們需要明白α（指數平滑常數）和N（移動平均的時期個數）之間的關係。