e2 Sanjeev Bordoloi 服務管理：運作、戰略與信息技術 v9

14.5.2　簡單指數平滑法

簡單指數平滑法（simple exponential smoothing）是時間序列模型中用於需求預測的最常用方法。它也可以“剔除”數據中偶然出現的因素，但是優於N期移動平均法。主要優點表現在三個方面：①舊數據不會被有意刪掉或丟失；②越舊的數據權重越低；③計算簡單，僅需要最新的數據。

簡單指數平滑法的基礎是：反饋出預測的錯誤，糾正以前的平滑值。在式（14-3）中，S_t是t時期的指數平滑值，A_t是t時期的實測值，α是平滑常數，取值一般在0.1～0.5之間。

（A_t-S_t-1）項是實測值和計算出來的前期指數平滑值的差值，它表示預測的誤差。將其乘以α再加上前期的平滑值，就得到新的指數平滑值S_t。值得注意的是，預測誤差的取值可正、可負，那麼此時該方法是怎樣自我糾偏的呢？

通過對錶14-2中的入住率做移動平均，我們發現最近兩個星期六平均入住率確有提高。在表14-3中列出相同的數據，同時在第三欄中列出每一時期的實測值（A_t）。運用簡單指數平滑法，可以再次發現平均入住率確實有顯著變化。

表14-3　簡單指數平滑法［旅店星期六的入住率（α=0.5）］

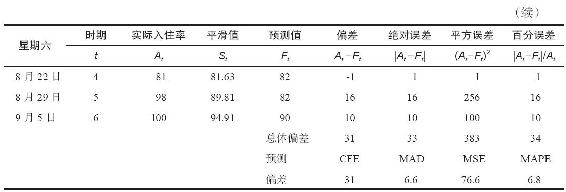
因為必須從某一處開始計算，所以就把一系列數據中的第一個實測值A_t作為第一個平滑值S_t。如表14-3所示，8月1日的S₁=A₁=79.00。8月8日的平滑值S₂可以根據式（14-3），即8月8日的實測值A₂和8月1日的平滑值S₁得出。我們設定α=0.5，如下所述，該結果與使用三時期移動平均法得到的結果類似：

採用類似的計算方法可以得出接下來各期的平滑值（S₃，S₄，S₅，S₆）。

簡單指數平滑法假定數據的分佈是依據一個恆定的均值形成的。因此，對計算出的第t時期平滑值取整可以作為t+1時期的預測值，即：

8月8日的平滑值是81.50，那麼8月15日入住率的最佳預測是81.50。值得注意的是，預測誤差（84-79）是+5（也就是說，我們低估了5個百分點的需求）。把前一個平滑值加上誤差值的一半，就可以提高新的平均入住率的估計值。這種將誤差反饋回來以修正以前估計的思想來源於控制論。

表14-3中所示的平滑值是在α=0.5時計算出來的。當然，如果我們希望平滑值受最新的數據影響更小，可以對α取更小的值。圖14-1顯示α取0.1或0.5時，怎樣修勻真實值曲線。從圖中不難發現，平滑曲線（特別是α=0.5時）已經修勻了極點（即最低點、最高點），並且對近兩個星期六上升的入住率有所反映。因此，基於平滑值的預測可以防止對實測值中的極點產生過度反應。

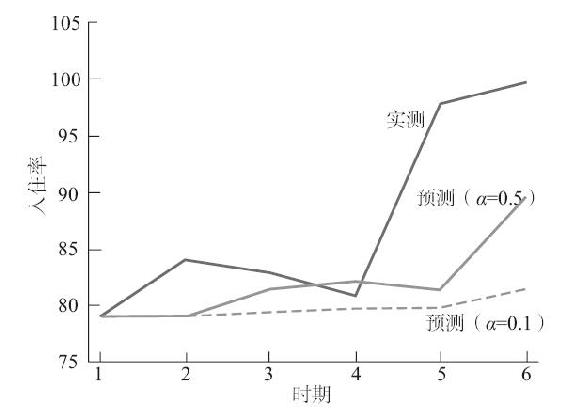
圖14-1　簡單指數平滑法：旅店星期六的入住率(α=0.1和α=0.5)

式（14-3）可重新寫為：

觀察一下式（14-5）中對過去數據給定的權重，就會理解“指數平滑”的意思了。我們發現給A_t以一定的權重α來決定S_t，通過替代不難看到A_t-1的權重為α(1-α)。通常，實測值A_t-n的權重為α(1-α)ⁿ。在圖14-2中，我們將過去一段時期的實測值權重的指數衰變描繪成線。值得一提的是，它不像N期移動平均法，應用它時舊的實測值不會從S_t的計算中完全消失，但是其重要性會逐漸降低。

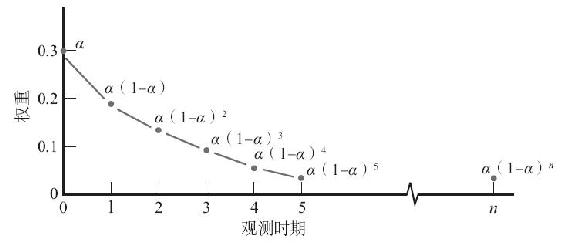
圖14-2　指數平滑法(α=0.3)中過去數據權重的確定