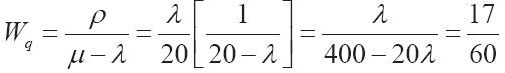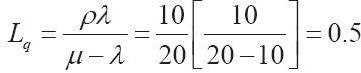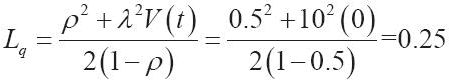e2 Sanjeev Bordoloi 服務管理:運作、戰略與信息技術 v9
例題
1.計算系統特徵值
問題陳述
夕陽航空公司準備開展主題為“一張機票,兩人旅行”的促銷活動,公司正為此而重新考慮其檢票程序。目前只有一名檢票員負責檢查行李和發放登機憑證,每位乘客通過檢票口平均需要3分鐘。服務時間服從負指數分佈,乘客到達數服從泊松分佈,在登機期間的預期平均值為每小時15人。
(1)乘客到達後不用等待,可立即接受服務的概率是多少?
解答
這是一個M/M/1排隊系統,λ=每小時15人/小時,μ=60/3=20人/小時。利用式(I-1):
P(系統空閒)=P0=1-ρ
=1-(15/20)
=0.25
(2)目前航空公司檢票口前的空間只夠容納3名顧客,包括正在接受服務的1人。等待區域無法容納全部等待顧客的時間佔多大比例?
解答
利用式(I-2):
P(等待空間不夠大)=P(n≥4)=ρ4
=(15/20)4=0.316
因此,在32%的時間裡,這個等待區域不夠大。
(3)由於預計到需求將會增加,公司決定,當顧客在隊伍中的平均等待時間達到17分鐘時,就增加一名檢票員。在檢票口可記錄顧客的到達率,請確定每小時的到達率為多少時,就表明需要再增加一名檢票員。
解答
令式(I-8)等於17/60,代入μ=20,解得λ:
所以,λ=17人/小時。
2.能力規劃
問題陳述
乘客的平均到達率已達到每小時20人,夕陽航空公司必須再增加一名檢票員以提高其檢票系統的服務能力。根據對乘客進行的調查,乘客認為排隊等待的機會成本是每小時15美元。檢票員的工資是每小時10美元,每位乘客通過檢票口仍需要3分鐘。評估下列檢票系統方案,確定在哪一種方案下,檢票員和乘客排隊等待的每小時總成本最小。
(1)考慮一個多排隊結構,等待隊伍互相獨立,不存在乘客在隊伍之間移動的情況。假設兩個檢票口的服務需求相等,這種方案下的小時總成本是多少?
解答
將每條隊伍視為一個獨立的M/M/1排隊模型,系統的總成本即為單一隊伍成本的2倍。利用式(I-5)計算Lq的值,代入式(13-7),求出隊伍的成本:
所以,系統總成本=2[10+15×0.5]=35美元每小時。
(2)考慮增加一臺自動檢票機(ATM)與第一名檢票員一起檢票,檢票機的服務時間為常數3分鐘。假設服務需求平均分佈在檢票員和檢票機兩個入口處。如果自動檢票機的操作成本可以忽略不計,該方案的每小時總成本是多少?
解答
兩條隊伍互相獨立,一個同上一問一樣,是一個M/M/1排隊模型,Lq=0.5;另一個為M/D/1排隊模型(自動檢票機勻速服務)。
首先,令V(t)=0,利用式(III-2)計算自動檢票口的隊伍的Lq:
所以,系統總成本=檢票員成本+自動檢票機成本=10+15×0.5+0+15×0.25=21.25美元/小時。
(3)考慮兩名檢票員、一條隊伍的方案。這種方案的每小時總成本是多少?
解答
由附錄C可知,c=2,ρ=20/20=1。所以,可查出Lq=0.333,故系統總成本=10×2+15×0.333=25美元/小時。