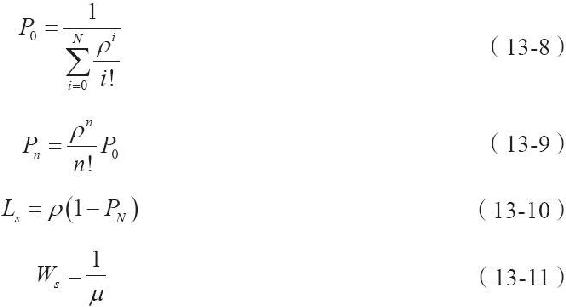e2 Sanjeev Bordoloi 服務管理:運作、戰略與信息技術 v9
13.4.4 由於等待區域過小造成銷售損失的概率準則
這一計劃準則更多地考慮等待區域的容納能力,而非提供服務的能力。等待區域過小可能導致潛在顧客退出該系統,轉向其他地方尋求服務。尤其在到達的顧客能夠看到等待區域的情況下,要經常考慮這個問題,例如餐館旁的停車場,或者是路邊銀行的車道。分析這些系統時,應利用有限排隊的M/M/c模型來估計退出系統的顧客數。
如果系統中允許的顧客數最多為N個,那麼,PN就是一位顧客到達後發現系統中人數已滿的概率。因此,PN代表了由於等待區域過小造成的銷售損失的概率,λPN則代表了單位時間內預期銷售損失數。現在,我們可以將由於等待區域過小造成銷售損失的成本與擴大等待區域可能需要的投資做一比較。
⊙【例13-9】
商業區停車場
停車場是一個無排隊的多服務檯排隊系統;也就是說,我們可以把停車場看作一個每個停車位就是一個服務檯的服務系統。當車位已滿後,接下來到達的顧客就會被拒絕,因為該系統不允許排隊。所以,一個停車場就是一個排隊能力為零的有限排隊系統,因為N=c。
根據這個模型,一位事業心很強的學生注意到,在中央商業區有一塊空地可以利用。這個學生從房地產經紀人那裡瞭解到,這塊地的主人正打算把它作為一個停車場租賃出去,租金為每天50美元。對該地區的交通狀況進行一番觀察之後,學生髮現,在這塊空地對面的一家百貨商店的車庫中,每小時約有10輛車找不到停車位。車庫管理員反映說,顧客大約會花1個小時在百貨商店購物。為了計算這一方案的可行性,學生假設到達的顧客服從泊松分佈,顧客購物的時間服從指數分佈。由於停車場只有6個停車位,學生想知道商場會因此失去多少潛在的生意機會。
我們可以把這個停車場看作一個不允許排隊的M/M/c有限排隊系統。所以,用M/M/c有限排隊系統的公式進行計算時,c=N。將c=N代入式(VI-1)(VI-2)(VI-4)和(VI-7),可以得到無排隊情況下的結果(如LQ=WQ=0)。其他公式不適用。
代入λ=10、N=6、μ=1,利用式(13-8)可以計算出P0=0.000349,利用式(13-9)可以計算出P6=0.48。因此,在每小時到達的10位顧客中,大約一半的人(10×0.48=4.8)會發現車位已滿。因此,這個擁有6個停車位的停車場只能滿足大約一半的服務需求。
⊙服務標杆
不要瞎猜,模擬!
模擬不僅僅是用來研究排隊系統的計算機模型。的確,模擬對於探索和測試“假設”場景以改進服務運行非常有用。然而,電信巨頭美國電話電報公司(AT&T)卻以非常不同的方式運用了模擬。
該公司使用BTS高度定製的業務模擬,以促進AT&T戰略執行計劃。3該計劃的一些目標是加強跨職能和業務單元的協作,解決實際的業務問題,在員工之間建立更強大的網絡,並激勵公司的員工。這個模擬包括四個團隊的員工之間的競爭,他們首先提出並評估各種能力,例如交叉銷售和開放Web功能,然後探索各種跨業務的計劃,最後考慮他們建議的實施及其對員工敬業度和顧客滿意度的影響。
美國電話電報公司還將“動手”模擬作為其網絡災難恢復系統的一部分。4在美國、英國和德國的許多地方,僱員們每季度進行一次災難演習模擬。其中一些模擬涉及恢復操作、無線應急通信、特殊操作(Hazmat響應)、顧客/機構拓展、事件管理和技術/災難恢復實現。在實際的模擬演練中,員工組成團隊,從不同的倉庫部署並組裝設備。然後,這些設備被安裝在大型拖車中,精確地複製那些被人為災害或自然災害破壞的基礎設施。在一個人們和企業的日常生活極其依賴於快速信息流的時代,美國電話電報公司為不斷提高其應急響應能力而做出的努力尤其重要。