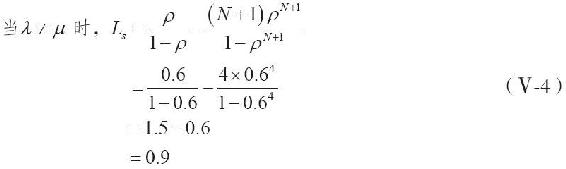e2 Sanjeev Bordoloi 服務管理:運作、戰略與信息技術 v9
13.3.6 有限排隊的M/M/1模型
有限排隊的M/M/1模型是對標準M/M/1模型的一種調整,即限制系統中允許的顧客數。假設允許的最大顧客數為N;這樣一來,如果當一位顧客到達時,系統中已經有N位顧客,那麼他不會尋求服務而是離開。這類有限排隊的例子如電話交換臺,如果所有的電話線路都已被佔用,此後再撥打該電話的人們就只能聽到忙音。除了有限能力這一特徵之外,標準M/M/1模型的其他假設仍然適用。應當注意的是,這時服務強度ρ有可能超過1。此外,PN代表顧客不加入系統的概率,λPN為預期損失的顧客數。
這一特殊模型在估算由於等待區域過小或隊伍過長造成的銷售額損失時十分有用。在例13-2船碼頭的例子中,假設等待區域只能容納2輛拖船;於是,系統中N=3。如下所示,利用附錄D中的式(Ⅴ-1)和式(Ⅴ-3),我們就可以分別計算出當N=3、ρ=0.6時,系統中有0、1、2和3位顧客的概率:

請注意,概率分佈的和為1.00,這表明我們已經囊括了所有可能的系統狀態。n=3的系統狀態發生的概率為10%。在到達率為每小時6人的情況下,每小時會有0.6人(6×0.10)由於沒有泊船位而到其他地方去停船。如下所示,通過式(Ⅴ-4),我們可以計算出預期系統中具有的顧客數(Ls)為0.9。這個數字大大小於無限排隊模型中的Ls,即1.5,因為在到達的顧客中,平均只有90%的人會得到服務。