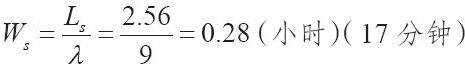e2 Sanjeev Bordoloi 服務管理:運作、戰略與信息技術 v9
13.3.3 標準M/M/c模型
圖13-4提供了M/M/c排隊模型的結構示意圖,展示了c個服務檯並行工作的狀況(用“·”表示),每個服務檯有一個顧客正在接受服務。泊松分佈的平均到達率為λ,箭頭表示未來將有顧客站在隊尾。虛線箭頭表示隊首的顧客會移動至第一個空閒的服務檯,服務檯下有一個箭頭用以表示平均服務率μ,並意味著每一個服務檯都一樣。此圖顯示在隊伍中等待的顧客有3個(Lq),假設只有2個服務檯,系統中有5個顧客(Ls)。研究單一與多服務檯排隊系統公式的應用時,需將這一示意圖牢記在心。
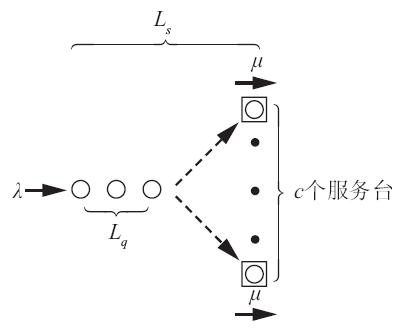
圖13-4 M/M/c排隊模型結構示意圖
標準M/M/c模型的假設前提同標準M/M/1模型一致,除此之外還有一條,即不同服務檯的服務率是互相獨立並且相等的(即認為所有的服務檯都是相同的)。和前面一樣,ρ=λ/μ;但是,這時平均正接受服務的顧客數ρ必須小於服務檯的數目c才能達到穩定狀態。如果將系統利用率指標定義為λ/cμ,那麼對於任何穩定狀態的系統,利用率指標都在0與1之間變動。圖13-5描繪了Ls作為利用率指標和平行服務檯數目c的函數的特徵曲線。這些曲線生動地論證了,當試圖充分利用服務能力時,會產生過度擁擠的現象。
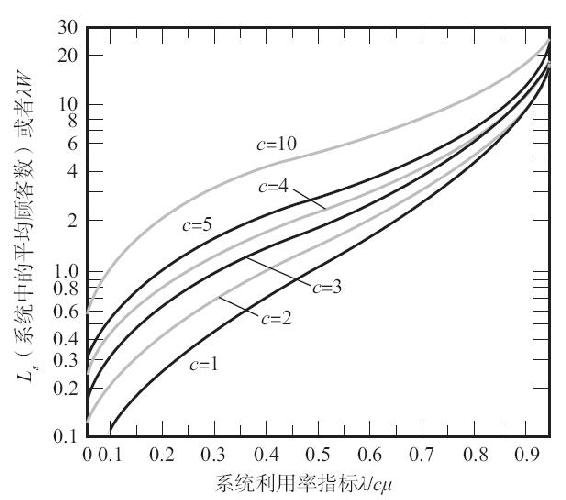
圖13-5 M/M/c模型中的Ls曲線
這一組曲線還說明,當通過增加平行服務檯的數目來減少擁擠現象時,系統的收益與增加的服務檯數目不成比例。例如,一個單一服務檯的系統(c=1)利用率指標為0.8。從圖13-5中可知,Ls的值為4。增加一個完全相同的服務檯,就產生了一個雙服務檯的系統,這時的利用率指標降低了一半,為0.4。圖13-5還表明,成倍增加服務檯數目會使擁擠現象減少400%,Ls≈1。
現在,我們不增加第二個服務檯,而是使單一服務檯系統的服務率加倍,從而使利用率指標降至0.4。從圖13-5中可知,這個超強服務系統的Ls≈0.67,但是,減少Ls的額外收益是以增加預期排隊人數(Lq從0.15增加到0.27)為代價的,見表13-2。這並不奇怪,因為一個單一服務檯系統必然會使排隊等待的人數增多。在服務能力相同的多服務檯系統中,由於能使更多的顧客接受服務,所以,排隊的顧客數相應減少了。因此,決定使用一個超強服務檯還是使用若干個平行服務檯實現相同的服務能力,就取決於對預期排隊等待時間或預期逗留時間的考慮。
第11章中曾提到,設法減少顧客排隊時的等待時間通常是可取的,尤其是人們必須排在一條有形的隊伍中時更應如此。而且,一旦開始接受服務,顧客對於時間的態度就會改變,因為這時顧客自身是注意力的焦點。不過,在計算機主機開發的早期,大學通常會採用一箇中心計算機系統為整個學校服務,因為這時首要的考慮是週轉時間(即在系統中逗留的時間)短、計算能力強。
表13-2 服務能力加倍的結果

①系統利用率。
為了實現服務的規模經濟,一種方法是將全部服務能力合併為一個超強服務檯;另一種方法是服務集合(pooling services),即將多個獨立的服務檯集中到一箇中心位置,組成一個服務單元。
⊙【例13-3】
祕書集合
某個規模較小的商學院有四個系:會計系、金融系、營銷系和管理系,每個系都設有一名祕書,他們負責打印班級材料,且只為本系教職工提供服務。但是,院長經常聽到教職工向他抱怨,說交給祕書的工作總是要拖延很長時間才能完成,會計系教職工的意見尤為強烈。於是,院長派他的一名助手去各系蒐集到達率和服務時間的數據。對數據進行分析後,助手報告說,祕書工作的到達數服從泊松分佈,其中會計系的平均到達率λ為每小時3件工作,其餘三個系均為每小時2件工作。無論工作來自哪個系,完成一件工作的平均時間都是15分鐘,服務時間服從指數分佈。
由於有預算限制,不允許再增聘祕書。不過,院長相信,如果將所有的祕書集中起來,面向整個商學院的教職工接受工作任務,服務狀況一定可以得到改善。所有的工作請求不論來自哪個系,都集中到一個地方;按照先到達者先服務的原則,由第一位出現空閒的祕書處理。在公佈這個方案之前,院長讓那名蒐集數據的助手分析一下現有系統的績效,並與祕書集合這個備選方案進行比較。
現有系統是四個基本上獨立的單一服務檯的M/M/1排隊系統,每個系統的服務率μ均為每小時4個任務請求。評價系統績效最恰當的指標應當是教職工預期在系統中的逗留時間或是週轉時間。到達率的不同可以解釋為什麼會計系的教職工尤其為工作拖延而煩惱。利用M/M/1模型中的公式Ws=1/(μ-λ),我們得知,在各系分別設立一個獨立祕書的情況下,會計系教職工的平均週轉時間Ws=1/(4-3)=1.0(小時),即60分鐘;而其他系的教職工的平均週轉時間Ws=1/(4-2)=0.5(小時),即30分鐘。
本例中把祕書集合起來的建議實際上形成了一個多服務檯、單一排隊的系統,或稱為M/M/4系統。到達率為各個繫到達率之和(2+2+2+3),即λ為每小時9個工作請求。
因為M/M/c模型的計算過程過於複雜,所以我們通常使用附錄C“M/M/c排隊模型中的Lq值”來求解Lq。在這個問題中,c=4,ρ=9/4=2.25,我們可以利用插值法求出Lq=0.31,所以,Ls=Lq+ρ=2.56。
使用式(13-5):
預期週轉時間從30分鐘(對於會計系教職工來說是60分鐘)大幅度縮減為17分鐘,可以想象,這一方案很容易贏得教職工的擁護。
服務集合的優點是更好地利用了空閒的祕書。在各個系中分別設有一個系統的情況下,存在四個獨立的隊,這就有可能出現某個系的祕書被排起長隊的工作壓得喘不過氣來,另一個系的祕書卻無所事事。如果一項正在等待的工作請求被轉給空閒的祕書,這項工作就會立即得到處理。等待隊伍從4條變為1條,只要存在等待服務的工作請求,系統就不允許祕書出現空閒,這就避免了利用率低的問題。
正是由於認識到出現擁擠現象的原因是到達率及服務時間的差異性,集合服務資源的做法才會獲得成功。從整個系統的角度來看服務過程,一個地方的暫時空閒可以用來緩解另一個地方因為需求突然膨脹或工作十分費時而引起的擁擠現象。另外,可以投入使用卻沒有使用的服務檯空閒意味著損失了服務能力,並會導致用顧客等待來衡量的服務質量的下降。集合的概念不僅適用於不同位置的服務檯,在實踐中,它還表現為銀行和郵局通常讓顧客排成一隊,而不是分別排在每個營業窗口前。從理論上說,單一隊伍會比多條隊伍的平均等待時間短,但是,一條長長的隊伍可能給顧客造成需要等待很久的感覺。這就是麥當勞不採用這種方式的原因:它擔心顧客進門後,看到一條很長的隊伍,會因而萌生退意。
如果要將服務資源集中到一個離顧客很遠的位置,那麼是否採用這種方式就應多加考慮。本例中,評估該方案時,應當把教職工走到服務地點的預期時間計算在預期等待時間內。對於緊急事項的服務來說,通常做法是將服務檯分散於整個服務區中,而不是將它們聚集於一箇中心位置。救護車服務系統就是一個很好的例子,通過分散的服務檯來滿足儘量縮減應急反應時間的需要。