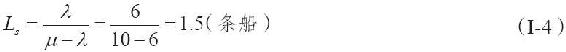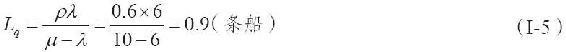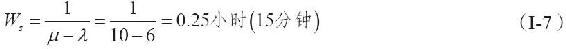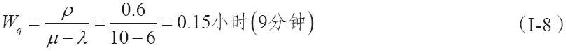e2 Sanjeev Bordoloi 服務管理:運作、戰略與信息技術 v9
13.3.2 標準M/M/1模型
每一個排隊模型對各項排隊系統特徵(即需求群體、到達過程、排隊結構、排隊規則和服務過程)都規定了具體的假設前提。因此,任何一個排隊模型的運用都只有在符合其假設前提時才有效。標準M/M/1模型的推導需要對排隊系統做如下假設:
(1)需求群體。到達的顧客總數無限或非常大。需求服務的顧客互相獨立,並且不受排隊系統的影響(如不需要預約);
(2)到達過程。到達間隔時間服從負指數分佈,或者到達率服從泊松分佈;
(3)排隊結構。只有一條等待隊伍,對隊長無限制,不存在退出隊伍或在隊伍之間移動的情況;
(4)排隊規則。先到達者先服務(FCFS);
(5)服務過程。只有一個服務檯,其服務時間服從負指數分佈。
圖13-3提供了M/M/1排隊模型的結構示意圖,展示了單一服務檯,即只有一個顧客接受服務的狀況,圖中用一個方框中包含一個圓圈表示。泊松平均到達率為λ,箭頭表示未來將有顧客站在隊尾。服務檯下有一個箭頭用以表示平均服務率μ。整張圖顯示在隊伍中等待的顧客有3個(Lq),在系統中的顧客有4個(Ls)。我們研究單一服務檯排隊系統公式的應用時,需將這一示意圖牢記在心。
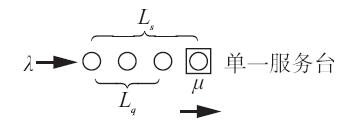
圖13-3 M/M/1排隊模型結構示意圖
只需知道平均到達率λ和每個服務檯的平均服務率μ,就可以利用附錄D列出的公式計算出系統的績效特徵。這些公式清楚地說明了,為什麼在單一服務檯模型中平均服務率μ總是要大於平均到達率λ(即能力必須超過需求)。如果不是這樣,如μ等於λ,運行特徵的平均值就無法根據定義求出,因為求解平均值的所有公式都是以(μ-λ)為分母。理論上來講,對於無限長的排隊情況,系統永遠不會達到穩定狀態。
⊙【例13-2】
船碼頭
特拉維斯湖岸邊有一個船碼頭,人們從這裡把他們的小船拖到娛樂地點去。通過對帶小船來到碼頭的汽車進行調查,我們發現每天早晨到達的遊客服從泊松分佈,每小時的平均到達率λ=6條船。再對蒐集到的發船時間數據進行測試,證實平均每條船需要花6分鐘,服從指數分佈(相當於每小時服務率μ=10條船)。如果M/M/1模型的其他假設都成立(即,無限的需求群體,沒有隊長限制,不存在退出或移動,先到達者先服務的排隊規則),那麼我們就可以利用附錄D的公式(在此也列出)來計算這個系統的特徵:
(注:ρ=λ/μ=6/10=0.6)
系統繁忙,顧客到達後需等待的概率(即k=1):
碼頭空閒的概率是:
系統中的平均船隻數:
平均排隊船隻數:
系統中的平均逗留時間:
平均排隊時間:
通過計算我們發現,船碼頭在60%的時間裡都很繁忙。因此,只有在40%的時間裡(即當碼頭空閒時),來到碼頭的遊客可以直接拖船下水而不必等待。這些計算結果具有內在一致性,因為在系統中的平均逗留時間(Ws)15分鐘是平均排隊時間(Wq)9分鐘與平均服務時間6分鐘二者之和。到達碼頭的遊客將會發現,系統中有1.5條船(Ls),而預期排隊的船隻數為0.9條船(Lq)。預期的排隊船隻數加上正在碼頭髮船的船隻數就等於預期系統中的船隻數。但是,預期正在發船的船隻數不是1,而是系統繁忙的概率乘以一個服務檯,或者ρ(1)=0.6條船。每發出一條船的過程中的0.6條船加上平均排隊的0.9條船,我們就得到預期系統中有1.5條船。
注意,系統中的顧客數n是一個隨機變量,其概率分佈由式(I-3)確定,這個公式在附錄D也會列出,在這裡用(1-ρ)來代替P0:
系統中的顧客數還可以用來確定系統的狀態。例如,當n=0時,系統是空閒的;當n=1時,服務檯處於繁忙期,但沒有形成排隊;當n=2時,服務檯處於繁忙期,等待隊伍是1個人。n的概率分佈對於確定等待室的適當規模十分有用。
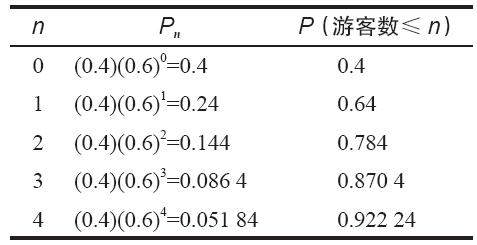
還以船碼頭為例,如果要保證每一位來到碼頭的遊客在等待接受服務時能找到地方停車的概率為90%,決定此時需要的停車空間。重複使用系統狀態的概率分佈,累積n的值,直至系統狀態概率的累積值超過90%為止。表13-1中的計算過程顯示,當n等於或小於4時,系統狀態為92%。這表明應當提供可容納4輛裝有船隻的拖車場地,因為在92%的時間裡,到達碼頭的遊客會發現已有3個(即4個減去1個正在接受服務)或以下的遊客排隊等候。
表13-1 決定所需的停車空間