e2 Sanjeev Bordoloi 服務管理:運作、戰略與信息技術 v9
13.3 分析型排隊模型
存在許多種不同的排隊模型。最常見的是用如下標記法將平行服務檯排隊模型進行分類,從這些標記法中可識別出A/B/C的三個特徵:A代表到達間隔時間的分佈,B代表服務時間的分佈,C代表平行服務檯的數目(如超市裡的收銀臺)。用來描述到達與服務時間分佈的符號有:
M——到達間隔時間或服務時間的指數分佈(相當於到達數或服務率的泊松分佈);
D——到達間隔時間或服務時間為常數;
Ek——形狀參數為k的愛爾朗分佈(Erlang distribution)(如果k=1,則愛爾朗分佈等同於指數分佈;如果k=∞,則愛爾朗分佈為一常數);
G——具有均值和方差的一般分佈(如正態分佈、均勻分佈或其他經驗分佈)。
因此,M/M/1是一個單一服務檯的排隊模型,其中到達率服從泊松分佈,服務時間服從指數分佈。這時,可以用A/B/C標記法來區分一個排隊模型應當屬於哪一類。我們還將進一步探討本模型的特殊形式,例如,由於空間有限使排隊長度受到限制(如停車場),或者潛在顧客數量很小(如公司食堂)。根據A/B/C標記法所劃分的特徵,圖13-2給出了我們將在本章中學習的六類分析型排隊模型。在每一個排隊模型中(如M/M/1),都有一組用羅馬數字編號的公式(如Ⅰ、Ⅱ、Ⅲ)。這些公式還將在附錄D“特定排隊模型”中列出,以便快速查詢參考。
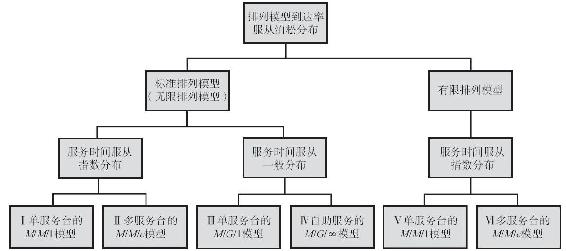
圖13-2 排隊模型的分類
最後,我們還將討論瞬變狀態和穩定狀態的概念。處於瞬變狀態時,系統的運行特徵值隨著時間的變化而變化;處於穩定狀態時,系統特徵值不隨時間的變化而變化,我們認為此時系統處於統計平衡。由於系統特徵依賴於初始狀態,因而在運行初期階段,系統特徵值通常是瞬變的。例如,試比較一家百貨商店在一個普通營業日開始營業的初始狀態和在年底促銷日開始營業的初始狀態,在後一種情況下,擁擠的顧客會使店員應接不暇。起初,排隊的人數會非常龐大,但是經過足夠長的一段時間後,系統會最終穩定下來。一旦達到了正常狀態,排隊人數就會服從於一個獨立於初始狀態的分佈,即達到統計平衡。附錄D中的所有排隊模型公式都假設處於穩定狀態。絕大多數服務系統是在動態的環境中運行的,有時到達率每個小時都在變化,因此,穩定狀態是很少能夠達到的。但是,穩定狀態的模型能夠為長期能力規劃決策提供有用的系統績效預測。
任何一個排隊模型的推導都有其假設前提。解析模型只有在符合這些假設的前提下,才適用於某一特殊環境。如果在某一應用環境中,假設是無效的(如,服從泊松分佈的到達率並不適用),那麼人們通常可以藉助計算機模擬方法來解決(見章末附錄“計算機模擬”)。
在決策過程中運用這些排隊模型時,會用到在附錄D中列示的排隊模型公式。這些模型中用到的符號及其含義如下:
n——系統中的顧客數;
λ——平均到達率(如每小時到達的顧客數);
μ——每個繁忙的服務檯的平均服務率(如每小時用顧客數表示的服務能力);
ρ——服務強度(λ/μ);
N——系統中可容納的最大顧客數;
c——服務檯的數目;
Pn——系統中恰好有n個顧客的概率;
Ls——系統中的平均顧客數;
Lq——平均排隊顧客數;
Lb——一個繁忙系統中的平均排隊顧客數;
Ws——顧客在系統中的平均逗留時間;
Wq——顧客的平均排隊等待時間;
Wb——顧客在一個繁忙系統中的平均排隊等待時間。