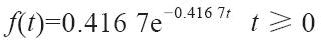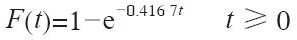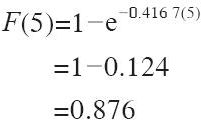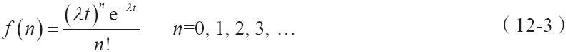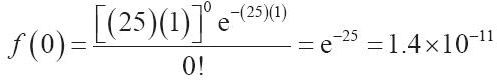e2 Sanjeev Bordoloi 服務管理:運作、戰略與信息技術 v9
12.5.2 到達過程
要想對服務系統進行分析,首先必須完整地瞭解服務需求的時間分佈和空間分佈。典型的方法是通過記錄實際到達次數來蒐集數據,這些數據將用來計算到達的間隔時間。許多實證研究表明,到達間隔時間呈指數分佈,圖12-3就是一個典型的指數分佈曲線。需要注意的是,起初的頻率很高,到右端則變成一條逐漸變細的長長的尾巴。理論上,指數分佈的平均值和標準差是相等的(如圖12-3中,μ=2.4,σ=2.6),也可以此來分辨指數分佈。
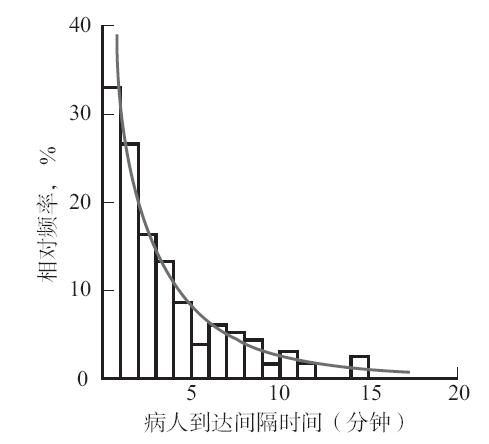
圖12-3 一所大學健康診所中病人到達間隔時間的分佈
資料來源:E.J.Rising,R.Baron,and B.Averill,“A systems Analysis of a University Health-Service Outpatient Clinic.”Reprinted with permission from Operations Research 21,no.5,September-October 1973,p.1038,Operations Society of America.No further reproduction permitted without the consent of the copyright owner.
指數分佈具有連續型的概率密度函數,其形式為:
式中 λ——一定間隔時間內的平均到達率(如分鐘、小時、天);
t——到達間隔時間;
e——自然對數的底數(2.718...);
平均值=1/λ;
方差=1/λ2。
累加的分佈函數為:
式(12-2)給出,到達時間間隔的數值為t,或者小於t。λ是到達間隔時間平均值的倒數。因此,在圖12-3中,間隔時間平均值為2.4分鐘,這就意味著λ等於1/2.4,即每分鐘到達次數為0.4167(即,平均每小時到達25位病人)。將0.4167代入λ,圖12-3中所列數據的指數分佈即為:
累積分佈為:
這樣就可以用式(12-4)求出,如果有一位病人已經到達,那麼在未來的5分鐘內再來一位病人的概率是多少。我們粗略地將5代入t,則
因此,在未來5分鐘內再來一位病人的可能性是87.6%。下次你到診所看病時,可以測試一下。
另一種分佈即泊松分佈,它與指數分佈有著密切的關係。泊松分佈是一種離散型的概率函數,其形式為:
式中 λ——一定間隔時間的平均到達率(如,分鐘、小時、天);
t——觀測的時間段的個數(通常t=1);
n——到達次數(0,1,2,...);
e——自然對數的底數(2.718...);
平均值=λt;
方差=λt。
泊松分佈給出了在t時間內有n位顧客到達的概率。按圖12-3給出的數據,代入λ=25,到達過程就可以用公式描述為:
這樣就可以分別求出每小時的時間間隔內有0,1,2,...位病人到達診所的概率。請注意,這裡我們把每分鐘的到達率λ=0.4167轉化為每小時的到達率λ=25。將0代入n,我們就可以計算出在一小時內沒有病人到達診所的概率:
這是一個非常小的概率。
圖12-4顯示了泊松分佈(即每小時病人的到達數)與指數分佈(即病人到達的間隔時間)之間的關係。正如我們所看到的,它們代表了同一過程的兩個方面。因此,到達的時間間隔服從平均值為2.4分鐘的指數分佈,就相當於每小時到達數服從平均值為25的泊松分佈(即60/2.4)。
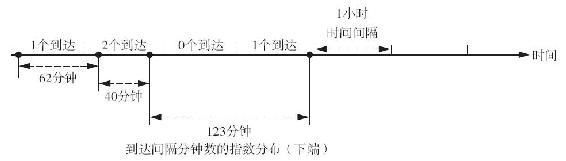
圖12-4 泊松分佈和指數分佈的對應關係
服務需求的數據通常是自動蒐集的(例如,通過高速公路上的路網),一段時間內的到達數被這段時間間隔的數字除,就得到單位時間的平均到達率。在單位時間不變的前提下,服務需求率應該是固定不變的(即λ是一個常數);否則,我們接下來就無法考慮服務需求率作為時間的函數潛在的波動情況。下列圖形反映了服務需求的這一動態特徵,圖12-5是一天中按小時表示的服務需求的波動情況,圖12-6是一週中各天波動的情況,圖12-7是一年中各月的波動情況。圖12-8則顯示了到達過程的分類。
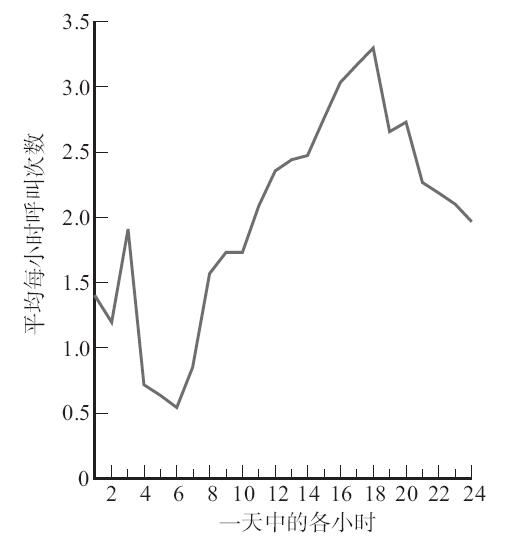
圖12-5 一天中各小時急救電話數
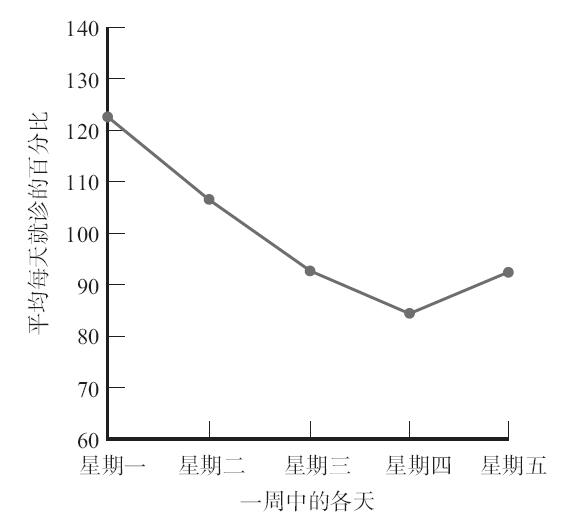
圖12-6 一週內各天中到達健康診所的病人數
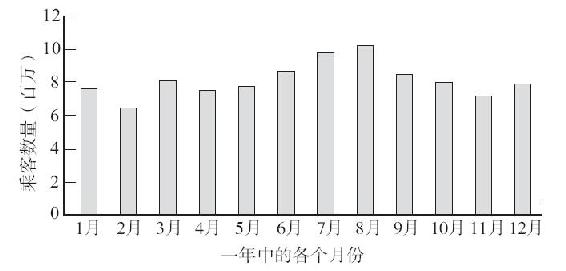
圖12-7 1994年各月份搭乘國際航班的乘客數
資料來源:http://www.bts.gov/oai/international/table1.txt.
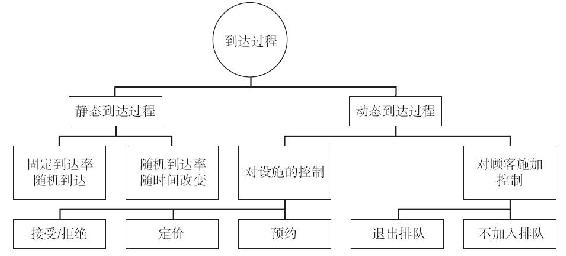
圖12-8 到達過程的分類
我們強調需求的頻率是時間的函數,但是需求的空間分佈同樣會有不同。如城市中的緊急救護車需求,由於需求群體會從居住區暫時轉移到工業和商業區上班,所以對於救護車的需求會存在空間上的轉移。