e1 Stephen Ross 公司理財 v12A
23.2 期權估值基礎
我們已經瞭解了看跌期權和看漲期權的基礎知識,接下來我們來討論決定其價值的因素。在接下來的討論中,我們將重點討論看漲期權,但同樣的分析也適用於看跌期權。
23.2.1 看漲期權在到期日的價值
我們已經討論了不同股票價格下看漲期權的收益。在後續討論中,我們將用到以下符號:
S1=到期日股票價格(在一個期間內)
S0=當日股票價格
C1=到期日看漲期權價值(在一個期間內)
C0=當日看漲期權價值
E=期權執行價格
從我們之前的討論可知,如果到期日股票價格(S1)低於執行價格(E),那麼到期日看漲期權價值(C1)為零。換句話說:
C1=0 若S1≤E
或者,等效地:
C1=0 若S1-E≤0 (23-1)
這種情況下,期權在到期日是沒有價值的。
如果期權是有價值的,那麼S1>E,同時到期日期權價值等於兩者的差額:
C1=S1-E 若S1>E
或者,等效地:
C1=S1-E 若S1-E>0 (23-2)
假設我們有一個執行價格為10美元的看漲期權。該期權即將到期。如果到期日該股票的價格為8美元,那麼我們有權選擇是否支付10美元購買價值僅為8美元的商品。因為到期日股票價格低於期權執行價格(S1≤E),我們的到期日期權價值為零。如果到期日股票價格為12美元/股,那麼該期權具有價值。因為我們可以以10美元/股購買股票,所以期權價值為每股S1-E=12-10=2美元。
圖23-1繪製了到期日看漲期權價值與股票價格的關係,結果看起來像曲棍球棒。請注意,對於每個小於E的到期日股票價格,到期日期權價值為零。對於每個大於E的到期日股票價格,到期日看漲期權價值是S1-E。此外,一旦到期日股票價格超過執行價格,到期日期權價值就會隨股票價格上升而上升。
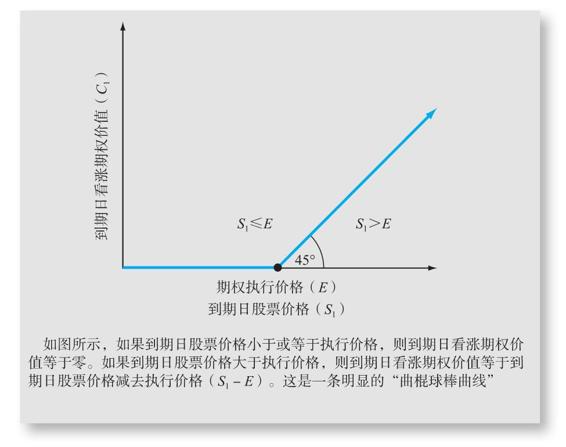
圖23-1 不同股票價格下的到期日看漲期權價值
23.2.2 看漲期權價值的上下限
我們已經知道如何確定C1,即到期日看漲期權價值,之後,我們研究一個更具挑戰性的問題:如何確定C0,即當日看漲期權價值?我們將在接下來的幾節中討論這個問題。現在,先確定看漲期權價值的上限和下限。
1.上限
看漲期權價值的上限是什麼?如果你考慮一下,答案是顯而易見的。看漲期權賦予你買入股票的權利,因此它的價值永遠不會高於股票本身。這告訴我們看漲期權價值的上限是:標的股票價格。其符號表示如下:
C0≤S0 (23-3)
2.下限
看漲期權價值的下限是什麼?這個答案不容易得出。首先,看漲期權不能小於零,所以C0≥0。此外,如果股票價格大於執行價格,則看漲期權價值至少是S0-E。
為什麼這麼說?假設我們有一個看漲期權,售價為4美元,股票價格是10美元,執行價格是5美元。此時存在盈利機會嗎?答案是肯定的,因為你可以以4美元購買看漲期權,並立即再花費5美元執行該期權。你獲得股票的總成本為4+5=9美元。如果你立即以10美元/股的價格轉手出售股票,那麼你將獲得1美元的特定利潤。
像這樣獲得無風險利潤的機會被稱為套利或套利機會。套利的人被稱為套利者,簡稱為“arb”。套利(arbitrage)一詞的詞根與仲裁(arbitrate)一詞的詞根相同,套利者實質上是對價格進行仲裁。當然,在正常健康的市場中,明顯的套利行為是罕見的。
對於看漲期權,為防止套利,當日看漲期權價值必須大於股票價格減去執行價格:
C0≥S0-E
如果我們把兩個條件放在一起,我們有:
C0≥0 若S0-E<0 (23-4)
C0≥S0-E 若S0-E≥0
這些條件表明,看漲期權的下限是0與S0-E兩者中的較大值。
期權的下限被稱為期權內在價值(intrinsic value),是期權立即履約時的價值。根據這個定義,到目前為止我們的討論可以重述如下:在到期日,期權的價值就是內在價值;一般來說,到期日前的期權價值高於期權內在價值。
圖23-2展示了看漲期權價值的上限和下限,還繪製了表示不同股票價格的看漲期權在到期日前的價值的曲線。該曲線的確切形狀和位置取決於許多因素。我們將在下一節開始討論這些因素。
23.2.3 一個簡單的模型:第一部分
下一章我們會詳細討論期權定價這個複雜的問題。而通常情況下,許多複雜問題可以通過一個簡單的例子來說明。假設我們正在研究一種看漲期權,期限為1年,執行價格為105美元。該股票目前售價為100美元/股,無風險利率Rf為20%。
當然,1年後股票的價值是不確定的。為簡單起見,假設我們知道股票價格要麼是110美元,要麼是130美元。值得注意的是,我們不知道這兩個價格出現的概率。換句話說,我們知道股票的可能價值,但不知道與這些價值相關的概率。
因為期權的執行價格是105美元,所以這個期權的價值要麼是110-105=5美元,要麼是130-105=25美元;但是,我們不知道是哪一個。然而,可以確定的是:這個看漲期權一定能兌現。
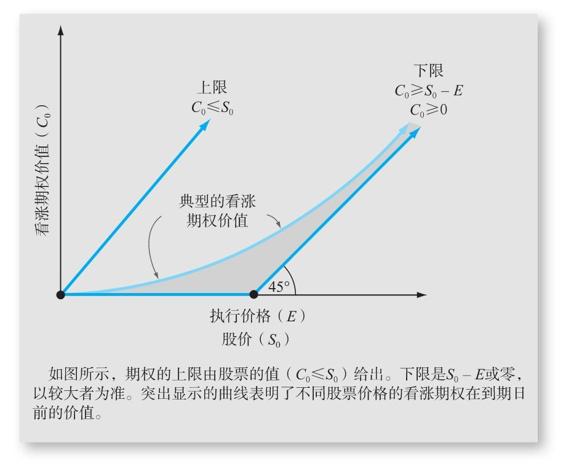
圖23-2 不同股票價格的看漲期權在到期日前的價值
1.基本方法
這個方法的關鍵點是利用期權和無風險資產的組合合理準確地複製股票的收益。怎麼做?具體操作是:購買一個看漲期權並將87.50美元投資於無風險資產(例如國庫券)。
一年後你會獲得什麼?你的無風險資產將獲得20%的收益,因此價值87.50×1.20=105美元。你的期權價值為5美元或25美元,因此總價值為110美元或130美元,與股票價值相同:

如圖23-2所示,這兩種策略(購買股票或買入看漲期權並投資於無風險資產)在未來具有完全相同的價值。
因為這兩種策略具有相同的未來價值,所以它們今天必須具有相同的價值,否則就會存在套利機會。因為該股票當天價格是100美元,所以當天看漲期權的價值C0是:
100=87.50+C0
C0=12.50(美元)
87.5美元是如何得到的?這是按無風險利率計算的期權執行價格的現值:
E/(1+Rf)=105/1.20=87.50(美元)
鑑於此,我們的示例顯示在這種簡單的情況下看漲期權的價值:
S0=C0+E/(1+Rf) (23-5)
C0=S0-E/(1+Rf)
也就是說,看漲期權的價值等於股票價格減去執行價格的現值。
2.稍複雜的情況
顯然,我們假設1年後的股價是110美元或130美元的情形過於簡單化了。現在,我們給出一個更加真實的模型,假設一年內股票的價格可以是大於或等於執行價格的任一值。另外,我們不知道不同價格出現的概率,但是我們確信這個期權最終會被履約。
仍然用S1代表1年後的股價。現在我們購買1份看漲期權和價值87.50美元的無風險資產。1年後,無風險資產價值105美元,期權價值S1-105,其具體價值將取決於股票價格。
當我們研究期權和無風險資產的組合價值時,我們發現了一些非常有趣的東西:
組合價值=無風險資產價值+期權價值=105+(S1-105)=S1
正如我們之前使用的方法,購買股票與購買看漲期權並將執行價格的現值投資於無風險資產的價值完全相同。
並且,為了防止套利,這兩種策略必須具有相同的成本,因此看漲期權的價值等於股票價格減去執行價格的現值:(注:你可能想知道如果股票價格低於執行價格的現值會發生什麼?結果是,這將導致看漲期權出現負值。而這是不可能發生的,因為期權最終會被兌現,所以我們確定股票價格在1年後至少是E。如果股票的當前價格小於E/(1+Rf),那麼股票的回報率必然大於無風險利率,這就創造了套利機會。例如,如果股票當前售價為80美元/股,那麼最低回報率將是(105-80)/80=0.312 5,即31.25%。因為我們可以以20%的利率借款,然後投資股票,最終可至少獲得11.25%的回報。因此,會出現套利機會。)
C0=S0-E/(1+Rf)
我們從這次討論中得出的結論是,只要我們確信期權會被履約兌現,就不難確定看漲期權的價值。
23.2.4 期權價值的四個決定因素
如果繼續假設期權會被兌現,那麼我們很容易就能確定決定期權價值的4個因素。而假如期權最終未被兌現,那麼還有第5個因素發揮作用。我們將在下一節討論第5個因素。
現在,如果我們假設期權在t期到期,則執行價格的現值為E/(1+Rf)t,並且該看漲期權價值為:
看漲期權價值=股票價值-執行價格現值 (23-6)
C0=S0-E/(1+Rf)t
我們看一下這個表達式,可以看出看漲期權的價值顯然取決於4個因素。
(1)股票價格。股票價格(S0)越高,看漲期權價值就越高。這並不奇怪,因為期權給了我們以固定價格購買股票的權利。
(2)執行價格。執行價格(E)越高,看漲期權價值越低。這也不足為奇,因為執行價格是我們為獲得股票而必須支付的價格。
(3)距到期日的時間。距到期日的時間(t)越長,期權價值越高。這又是顯而易見的,因為期權使我們有權在固定的時間內購買股票,隨著時間的增加,其價值也會上升。
(4)無風險利率。無風險利率(Rf)越高,看漲期權價值越高。這個結果有點不太明顯。通常情況下,我們認為資產價值會隨著利率的上升而下降。在這種情況下,執行價格是現金流出,是一種負債。負債的現值隨著貼現率的上升而下降。
概念問題
23.2a 到期日看漲期權的價值是多少?
23.2b 到期日前看漲期權價值的上限和下限是什麼?
23.2c 假設股票價格肯定大於看漲期權的執行價格,那麼看漲期權的價值是多少?為什麼?