e1 Stephen Ross 公司理財 v12A
13.7 證券市場線
我們現在來看看市場怎樣給風險以回報。首先,假定資產A的期望報酬率E(RA)為20%,貝塔係數βA為1.6,並且,假定無風險報酬率Rf為8%。根據定義,無風險資產沒有系統風險(或非系統風險),所以無風險資產的貝塔係數為0。
13.7.1 貝塔係數與風險溢價
考慮一個由資產A和無風險資產所構成的投資組合。我們可以通過改變在這兩項資產上的投資所佔的百分比,計算出一些可能的投資組合的期望報酬率和貝塔係數。例如,如果投資組合的25%投資在資產A上,那麼投資組合的資產報酬率就是
E(RP)=0.25×E(RA)+(1-0.25)×Rf=0.25×20%+0.75×8%=11%
同樣地,投資組合的貝塔係數βP為
βP=0.25×βA+(1-0.25)×0=0.25×1.6=0.40
請注意,因為權重的和必須等於1,因此投資在無風險資產上的百分比就等於1減去投資在資產A上的百分比。
有一件事情你可能會懷疑,投資在資產A上的百分比是否會超過100%?答案是肯定的。它之所以會發生,是因為投資者可以以無風險利率借款。例如,假設一個投資者有100美元,並以無風險利率8%另外借了50美元,那麼他對資產A的總投資就是150美元,也就是投資者總財富的150%。這種情況下的期望報酬率將為
E(RP)=1.50×E(RA)+(1-1.50)×Rf=1.50×20%-0.50×8%=26%
同樣,投資組合的貝塔係數βP為
βP=1.50×βA+(1-1.50)×0=1.50×1.6=2.4
我們也可以計算一些其他可能的情況,如下表所示:
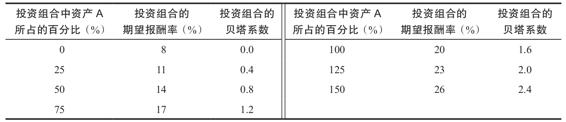
在圖13-2A中,標示了這些投資組合的期望報酬率和投資組合的貝塔係數。請注意,所有組合都落在同一條直線上。
1.風險回報率
圖13-2A中的直線的斜率是多少?與通常一樣,直線的斜率等於縱向上升的幅度與前進幅度之間的比值。在這個例子中,當我們從無風險資產移動到資產A時,貝塔係數從0上升到1.6(橫向增長1.6)。與此同時,期望報酬率從8%移動到20%,上升了12%。因此斜率為12%/1.6=7.5%。
請注意,這條線的斜率正好等於資產A的風險溢價E(RA)-Rf,除以資產A的貝塔係數βA
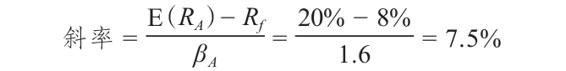
它告訴我們,資產A所提供的風險回報率為7.5%[1]。換句話說,對於每一“單位”的系統風險,資產A的風險溢價為7.5%。
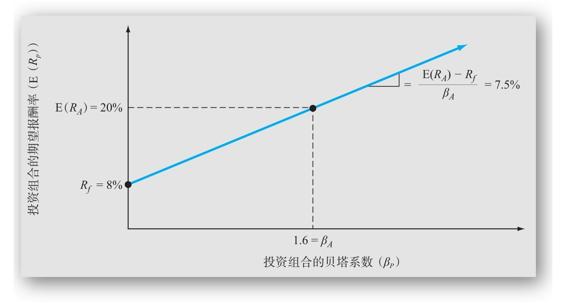
圖13-2A 資產A的投資組合期望報酬率和貝塔係數
2.基本觀點
現在假定我們考慮第2項資產:資產B。這項資產的貝塔係數為1.2,期望報酬率為16%。哪一項投資更好,資產A還是資產B呢?你可能會覺得我們實在沒辦法說:有些投資者可能偏愛資產A,有些投資者可能偏愛資產B。但是,實際上,我們可以說,資產A更好,這是因為,正如下面所證明的,至少相對於資產A來說,資產B所提供的報酬率不足以補償它的系統風險水平。
首先,我們計算資產B和無風險資產在不同組合下的投資組合期望報酬率和貝塔係數,就像對資產A所進行過的那樣。例如,我們投資25%在資產B上,其餘75%投資在無風險資產上,那麼這個投資組合的報酬率將為
E(RP)=0.25×E(RB)+(1-0.25)×Rf=0.25×16%+0.75×8%=10%
同樣,投資組合的貝塔係數βP為
βP=0.25×βB+(1-0.25)×0=0.25×1.2=0.30
下表列示了一些其他的可能性:
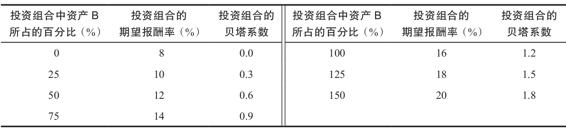
當我們把這些投資組合的期望報酬率和投資組合貝塔係數的組合繪製成圖13-2B時,就得到類似於之前我們對資產A畫的直線那樣的一條直線。
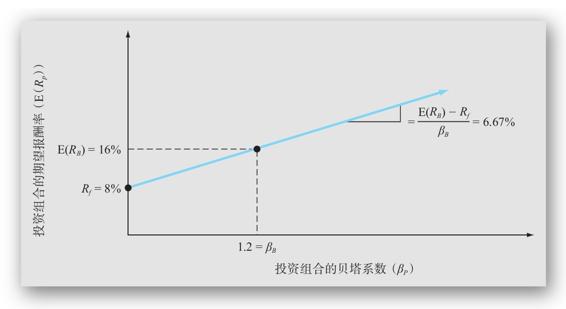
圖13-2B 資產B的投資組合期望報酬率和貝塔係數
一個值得注意的重要問題是,當我們比較資產A和資產B的結果時,如圖13-2C所示,代表資產A的期望報酬率和貝塔係數組合的直線位於代表資產B的直線之上。它告訴我們,在任何一個系統風險水平(以β來計量)下,資產A和無風險資產的一些組合總是會提供較高的報酬率。這就是為什麼我們說資產A是比資產B更好的投資。
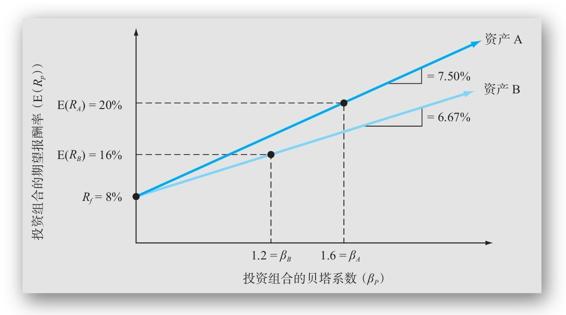
圖13-2C 兩個資產的投資組合期望報酬率和貝塔係數
我們還可以通過與資產B的斜率的對比,來看出資產A在給定的風險水平上能夠提供多高的報酬率
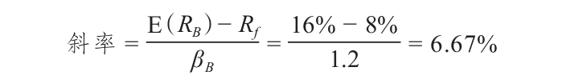
因此,資產B的風險回報率是6.67%,小於資產A的7.5%。
3.重要結論
我們所描述的資產A和資產B的狀況在一個健康運轉的活躍市場上不可能長期存在,因為投資者會被資產A所吸引,而排斥資產B。結果是,資產A的價格將會上升而資產B的價格將會下降。因為價格和報酬率的變動方向相反,因此資產A的期望報酬率將下降,而資產B的將上升。
這種買進和賣出的交易將一直持續到兩項資產剛好落在同一條直線上,它意味著市場對承擔風險給予相同的回報。換句話說,在一個活躍的、競爭性的市場,我們會得到這種情形
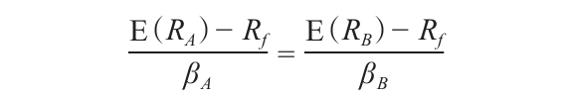
這就是風險和報酬率之間的基本關係。
我們的基本論點可以推廣到多於兩種資產的情境。事實上,無論我們有多少資產,我們總會得到這樣的結論:
市場上所有資產的風險回報率必定相等。
這個結論其實一點也不值得奇怪。舉例來說,它表明,如果一項資產的系統風險是另一項資產的2倍,那麼它的風險溢價也會是後者的2倍。
因為市場上所有的資產都具有相同的風險回報率,那麼它們必須在一條直線上。這個觀點展示在圖13-3中,如圖所示,資產A和資產B直接落在同一條直線上,因而它們具有相同的風險回報率。如果一項資產落在這條線的上方,例如圖13-3中的C點,它的價格將會上升,期望報酬率就會下降,直到它落在這條線上為止。同樣,如果一項資產落在這條線的下方,例如圖13-3中的D點,它的期望報酬率將會上升,直到它也正好落在這條直線上。另外,通常將資產期望報酬率與證券市場線之間的垂直距離稱為資產的“阿爾法”。
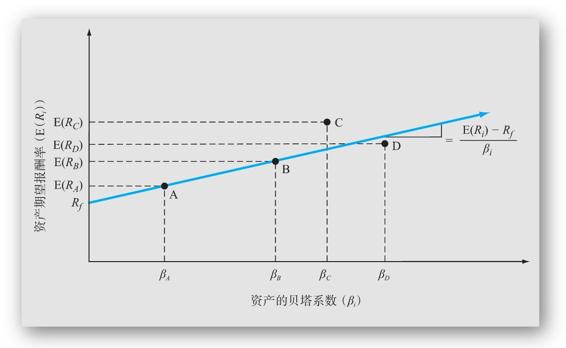
圖13-3 期望報酬率和系統風險
注:貝塔係數和期望報酬率的基本關係是,所有資產的風險回報率即(E(Ri)-Rf)/βi必定相等。這表明它們都落在同一條直線上。資產A和資產B就是展示這種關係的例子。資產C的期望報酬率太高,資產D則太低。
我們在這裡所提出的觀點適用於活躍的、競爭性的、運行良好的市場。如同NYSE這樣的金融市場就很好地滿足了這些標準。另外還有些市場,如實物資產市場,則可能這樣,也可能不這樣。基於這個原因,這些概念在考察金融市場時最有用。所以,我們在這裡主要考慮這種市場。然而,正如我們在接下來的章節中將要討論的一樣,從金融市場中蒐集到的有關風險和報酬率的信息,對於評價公司所做的實物資產投資至關重要。
【例13-7】低價買進,高價賣出
給定一項資產的期望報酬率和風險,如果它的價格太高,我們就說它被高估了。假設你發現了下表中的情形。
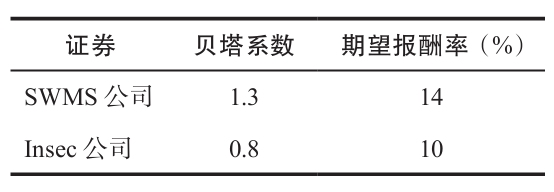
當前的無風險利率是6%,上面兩個證券中是否有哪一個的價值相對於另一個而言被高估了?
為了回答這個問題,我們計算了兩者的風險回報率。對於SWMS公司而言,這個比率為(14%-6%)/1.3=6.15%。對於Insec公司而言,這個比率是5%。我們所得到的結論就是,至少相對於SWMS公司而言,Insec公司在它的風險水平上所提供的期望報酬率不夠高。因為它的期望報酬率太低,所以價格太高了。換句話說,相對於SWMS公司而言,Insec公司被高估了。所以,相對於SWMS公司而言,我們預計Insec公司的價格將會下跌。請注意,我們可以說,相對於Insec公司而言,SWMS公司被低估了。
13.7.2 證券市場線
當我們把期望報酬率和貝塔係數描畫出來時,所得出的那條線顯然具有一定的重要性,所以現在我們得給它取個名字。我們用來描述金融市場中系統風險和期望報酬率之間關係的這條線,通常被稱為證券市場線(security market line,SML)。SML被認為是繼NPV之後,現代財務學中最重要的一個概念。
1.市場投資組合
瞭解SML等式是非常有用的。我們有很多種不同的方式來表述,但是其中有一種方式特別常見。假設我們考慮的是一個由市場上所有資產組成的投資組合。這樣的一個投資組合被稱為市場投資組合,我們將用E(RM)來表示市場投資組合的期望報酬率。
因為市場上所有資產都必定落在SML上,因此由這些資產組成的市場投資組合也必定落在SML上。要確定SML應該落在哪裡,我們需要知道市場投資組合的貝塔係數βM。因為這個投資組合代表市場上的所有資產,所以它必定擁有平均的系統風險。換句話說,它的貝塔係數是1。這樣我們就可以把SML的斜率表示成
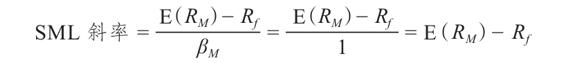
E(RM)-Rf通常被稱為市場風險溢價(market risk premium),因為它是市場投資組合的風險溢價。
2.資本資產定價模型
接下來,如果我們用E(Ri)和βi分別代表市場中任何資產的期望報酬率和貝塔係數,那麼我們知道這項資產必定會落在SML上。同樣地,我們知道它的風險回報率和整個市場的這個比率一樣
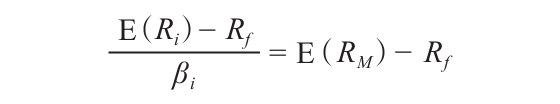
我們不妨把這個式子重新整理一下,就可以將SML等式寫成
E(Ri)=Rf+[E(RM)-Rf]×βi (13-7)
這個結果就是著名的資本資產定價模型(capital asset pricing model,CAPM)。
CAPM表明,一項特定資產的期望報酬率取決於三個方面。
(1)貨幣的純粹時間價值。它通過無風險利率Rf來計量,指你只是等待、不承擔任何風險的情況下所得的回報。
(2)承擔系統風險的回報。它通過市場風險溢價[E(RM)-Rf]來計量。這部分是市場對除了等待之外還承擔平均系統風險所給予的回報。
(3)系統風險的大小。它通過βi來計量。它是一項特定資產相對於平均資產而言,所面臨系統風險的大小。
順便提一下,CAPM適用於多種資產所組成的投資組合,就像它適用於單個資產一樣。在前面的部分,我們已經知道如何計算一個投資組合的β。只要把這個β代入CAPM等式中,就可以求出投資組合的期望報酬率。
圖13-4總結了我們對SML和CAPM的討論。照舊,我們畫出了期望報酬率和對應的貝塔係數。現在,我們發現,根據CAPM,SML的斜率等於市場風險溢價E(RM)-Rf。
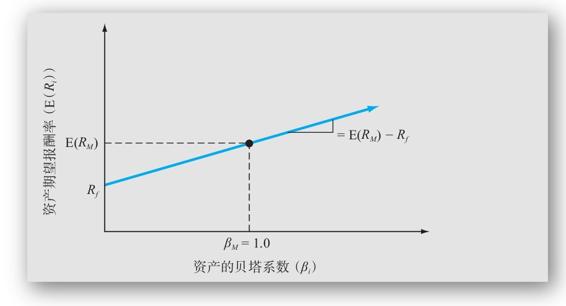
圖13-4 證券市場線(SML)
注:證券市場線的斜率等於市場的風險溢價,即承擔平均系統風險水平的回報。SML可以用等式來表示
E(Ri)=Rf+[E(RM)-Rf]×βi
這就是資本資產定價模型(CAPM)。
這總結了我們所提出的與風險–收益權衡(risk-return trade-off)有關的觀念。表13-9依照我們討論的順序對這些不同的觀念進行了總結,以備未來參考。
表13-9 風險和報酬率的總結


概念問題
13.7a 在運轉良好的市場中,風險和報酬率之間的基本關係是什麼?
13.7b 什麼是證券市場線?為什麼在一個運轉良好的市場中,所有資產都必定落在這條線上?
13.7c 什麼是資本資產定價模型(CAPM)?它告訴我們關於風險性投資必要報酬率的哪些內容?
【例13-8】風險和報酬率
假定無風險報酬率是4%,市場風險溢價是8.6%,某一隻特定股票的貝塔係數是1.3。根據CAPM,這隻股票的期望報酬率是多少?如果貝塔係數加倍,期望報酬率將變成多少?
貝塔係數是1.3,因此這隻股票的風險溢價是1.3×8.6%=11.18%。無風險報酬率是4%,因此期望報酬率為15.18%。如果貝塔係數加倍,變成2.6,風險溢價也將翻番為22.36%。因此,期望報酬率將變成26.36%。
[1] 這個比率有時也叫作特雷諾比率(Treynor index),這是用它的首創者之一的名字命名的。