e1 Stephen Ross 公司理財 v12A
13.1 期望報酬率和方差
在上一章中，我們討論過如何利用歷史數據計算平均報酬率和方差。現在我們開始討論當我們擁有關於未來的可能報酬率及其概率的信息時，我們如何分析報酬率和方差。
13.1.1 期望報酬率
我們從直觀的情形開始。考慮一個單獨的時期，比如說1年。我們有2只股票：L和U。這2只股票有以下特徵：股票L在第2年的期望報酬率為25%，股票U在第2年的期望報酬率為20%。
在這種情況下，如果所有投資者對報酬率的預期都相同，為什麼還有人願意持有股票U呢？歸根結底，為什麼在預期一隻股票會更好時還會投資於另一隻更差的股票呢？顯然，答案必須取決於兩種投資的風險。儘管我們期望股票L的報酬率為25%，但是它的實際報酬率很可能更高或更低。
例如，假設經濟很景氣。此時，我們認為股票L的報酬率將會是70%。如果經濟進入蕭條期，我們認為報酬率將會是-20%。在這種情況下，我們就說有兩種經濟狀況（states of the economy），它表示僅有這兩種可能的情況。當然，這樣的設定是過分簡化了，但是它使得我們不需要很多的計算就可以解釋很多關鍵的概念。
假設我們認為經濟景氣和經濟蕭條發生的可能性相同，都是50%的概率。表13-1列示了剛剛描述過的基本信息和關於股票U的另外一些信息。值得注意的是，股票U在蕭條時的報酬率為30%，在景氣期的報酬率為10%。
表13-1 經濟狀況與股票報酬率
很顯然，如果你購買這兩隻股票當中的一隻，比如說股票U，你在任何一年所能賺取的報酬率取決於這一年的經濟狀況。然而，假定概率不隨時間而改變。如果你持有股票U好幾年，那麼你將有一半的時間賺取30%的報酬，而另一半時間賺取10%的報酬。在這種情況下，我們說你對股票U的期望報酬率（expected return）E（RU），是20%。
E（RU）=0.50×30%+0.50×10%=20%
換句話說，你應該預期這隻股票平均可以賺取20%的報酬率。
對於股票L而言，概率是一樣的，但是可能的報酬率卻不相同。這裡，我們有一半的機會損失20%，另一半的機會賺取70%。那麼股票L的期望報酬率E（RL）就為25%。
E（RL）=0.50×（-20%）+0.50×70%=25%
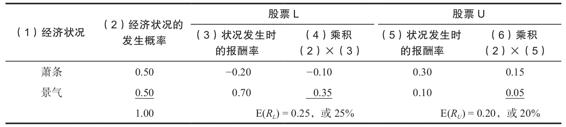
表13-2展示了這些計算。
表13-2 股票期望報酬率的計算
在上一章中，我們將風險溢價定義為風險投資和無風險投資的報酬率之差，並且計算了一些不同投資的歷史風險溢價。現在，利用預計報酬率，我們可以通過計算風險性投資的期望報酬率和無風險投資的具體報酬率之間的差，來得出預計的（projected），即期望的（expected）風險溢價。
例如，假設無風險投資的現行報酬率為8%，我們就可以說無風險報酬率（在這裡用Rf表示）是8%。給定這個數據，那麼股票U的預期風險溢價是多少呢？股票L的又是多少呢？因為股票U的期望報酬率E（RU）是20%，那麼預期風險溢價為
風險溢價=期望報酬率-無風險報酬率 （13-1）
=E（RU）-Rf=20%-8%=12%
同樣地，股票L的風險溢價=25%-8%=17%。
一般來說，某隻股票或其他資產的期望報酬率就等於所有可能的報酬率與它們的概率的乘積之和。因此，如果我們有100個可能的報酬率，我們將分別把每一個乘以它的概率，再將所有的結果加總。這樣得到的結果就是期望報酬率。風險溢價就是期望報酬率和無風險報酬率之差。
【例13-1】不相等的概率
回顧表13-1和表13-2，假設你認為經濟景氣發生的概率為20%，而不是50%。在這種情況下，股票U和股票L的期望報酬率是多少呢？如果無風險報酬率為10%，那麼風險溢價是多少呢？
第一件要注意的事情就是蕭條時期發生的概率為80%（=1-0.20），因為只有兩種概率的可能性。記住了這一點，我們發現股票U的報酬率為30%的概率是80%，報酬率為10%的概率為20%。為了計算期望報酬率，我們依然把可能的報酬率乘以概率，然後加總起來
E（RU）=0.80×30%+0.20×10%=26%
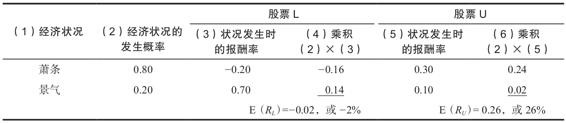
表13-3總結了兩隻股票的計算方法。請注意，股票L的期望報酬率是-2%。
股票U的風險溢價是26%-10%=16%。股票L的風險溢價是負的：-2%-10%=-12%。這有點奇怪，但也不是不可能，具體原因我們稍後討論。
表13-3 期望報酬率的計算
13.1.2 計算方差
為了計算兩隻股票報酬率的方差，我們首先求出距離期望報酬率偏差的平方。然後我們將每一個可能的偏差的平方乘以它的概率。將這些結果加總，得到的結果就是方差。標準方差通常是方差的平方根。
為了進一步說明，我們回到最開始討論的擁有20%期望報酬率的股票U。在一個給定的年份中，它的實際報酬率不是30%，就是10%。這樣，可能的偏差是30%-20%=10%和10%-20%=-10%。在這種情況下，方差是
方差=σ2=0.50×（10%）2+0.50×（-10%）2=0.01
標準差是方差的平方根
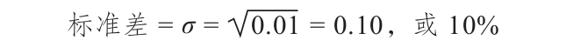
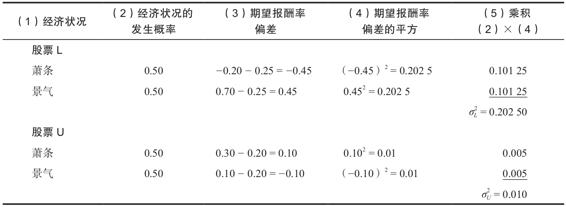
表13-4總結了這兩隻股票的計算。值得注意的是股票L的方差較大。
表13-4 方差的計算
當我們將期望報酬率和方差放在一起時，就得到如下表所示的結果。
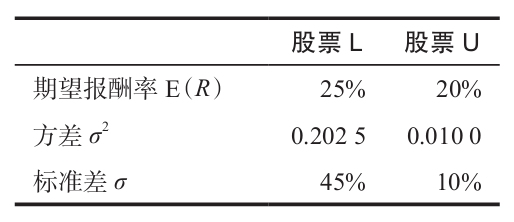
股票L的期望報酬率更高，但是股票U的風險更小。投資在股票L上，你將獲得70%的報酬率，但是也可能會損失20%。然而，投資在股票U上，你至少總會得到10%的報酬。
你應該購買這兩隻股票中的哪一隻呢？我們實在沒有辦法說，它取決於你的偏好。我們能夠合理地確信，有些投資者喜歡股票L勝過股票U，有些投資者喜歡股票U勝過股票L。
你可能已經注意到我們在這裡計算期望報酬率和方差的方法與上一章所用的方法多少有點不同。原因是，在第12章裡，我們所考察的是實際的歷史報酬率，因此我們是在一些真實的歷史事件基礎上計算平均報酬率和方差。而在這裡，我們預測了未來的報酬率及其概率，因此這才是我們所要處理的信息。
【例13-2】更多不相等的概率
回顧例13-1，如果發生的概率不相等，這兩隻股票的方差和標準差分別是多少？
我們可以把需要的計算總結如下：
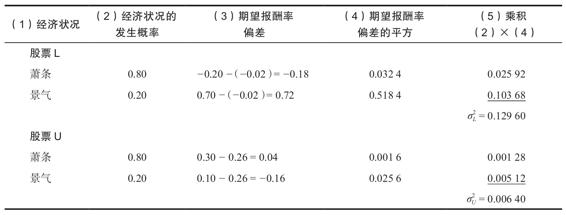
根據這些計算，股票L的標準差是σL=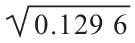
=0.36，或36%。股票U的標準差較小：σU=
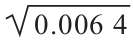=0.08，或8%。
概念問題
13.1a 我們如何計算證券的期望報酬率？
13.1b 我們如何計算期望報酬率的方差？