e1 Stephen Ross 公司理財 v12A
12.5 平均報酬率的進一步講述
到目前為止,在本章中我們密切關注了簡單的平均報酬率。但是有另外一種方法計算平均報酬率。事實上,用兩種不同的方法計算平均報酬率可能會導致某些混淆,因此我們在本節中的目標是解釋這兩種方法以及它們各自適用的情形。
12.5.1 算術平均與幾何平均
讓我們從一個簡單的例子開始。假設我們用100美元購買某隻股票。不幸的是,在你持有的第1年,它就下跌到了50美元。在你持有它的第2年,它又回升到了100美元,回到了你的起點上(沒有分派股利)。
那麼你的這項投資的平均報酬率是多少呢?根據常識來看,可能你會說平均報酬率應該恰好是零,因為你從100美元開始,最後又回到了100美元。但是如果計算逐年報酬率,我們發現你第1年損失了50%(你損失了一半的錢)。第2年你賺取了100%(你的錢翻了一番)。因此,你這兩年中的平均報酬率應該是(-50%+100%)/2=25%!
那麼究竟哪個是正確的,0還是25%?兩者都是對的:它們只是回答了不同的問題。0被稱為幾何平均報酬率(geometric average return),25%被稱為算術平均報酬率(arithmetic average return)。幾何平均報酬率回答的問題是“你在一定期間內每年的平均複利報酬率是多少”,算術平均報酬率回答的問題是“你在一定期間內一個平均年度的報酬率是多少”。
請注意,在前面的部分,平均報酬率是用算術平均法計算的,因此,我們已經知道如何計算它們了。現在我們需要做的是:①學會如何計算幾何平均報酬率;②學習在哪些情形下一種平均報酬率比另一種更有意義。
12.5.2 計算幾何平均報酬率
首先,來看看我們如何計算幾何平均報酬率。假設某一項投資在過去4年的報酬率分別為10%、12%、3%和-9%。那麼,這4年間的幾何平均報酬率為(1.10×1.12×1.03×0.91)1/4-1=0.036 6,或3.66%。相應地,算術平均報酬率為(0.10+0.12+0.03-0.09)/4=0.04,或4%。
一般地,如果我們有T個年度的報酬率,在這T年期間的幾何平均報酬率的計算公式為
幾何平均報酬率=[(1+R1)×(1+R2)×…×(1+RT)]1/T-1 (12-4)
這個公式告訴我們計算幾何平均報酬率需要以下4個步驟。
(1)找出T個年度的報酬率R1,R2,…,RT,並把每一個報酬率都加上1。(在把它們轉化成小數之後。)
(2)把第1步得出來的所有數字相乘。
(3)將第2步的結果開T次方。
(4)最後,將第3步的結果減去1,得到的結果就是幾何平均報酬率。
如其所言 傑里米J.西格爾的長線股票
我所收集的真實金融市場的報酬率的數據,最讓人著迷的特點就是長期實際股本報酬率的穩定性。1802~2013年美國股票的複合年均(幾何的)實際報酬率是6.7%,而這項報酬率在長期都保持著顯著的穩定性。1802~1871年,實際報酬率的平均值為6.7%;1871年,當考爾斯基金會(Cowles Foundation)的數據開始可用時,至1925年,股票的實際報酬率的年均值為6.6%;從1925年之後,當著名的伊博森數據出現之後,股票的實際報酬率的年均值為6.7%。儘管在“二戰”之後股價已經翻了10多倍,但是實際股票報酬率的年均值仍舊為6.8%。
股票實際報酬率的長期穩定性強烈地證明了股本報酬率的均值迴歸。均值迴歸意味著股票報酬率會在短期發生波動,但長期來看會表現出顯著的穩定性。當我的研究第一次出版時,關於股票市場報酬率的均值迴歸性質有很多質疑的聲音,但是現在這個概念被廣泛地接受了。如果均值迴歸這個概念盛行,那麼相比短期的投資組合,長期的投資組合中應有更大的比例是股權投資。這個結論在投資方面是長期存在的“傳統”觀點,但是它並不服從一個在20世紀七八十年代被學術界廣泛接受的概念,即股票報酬的隨機遊走。
當我的數據第一次出現,也引起了很多關於“生存偏差效應”的討論,事實上,美國的股票報酬率通常還是不錯的,因為美國是最成功的資本主義國家。但是3位英國研究人員,埃爾羅伊·迪姆森(Elroy Dimson)、保羅·馬什(Paul Marsh)、邁克爾·斯湯頓(Michael Staunton)研究了16個國家從20世紀初開始的股票報酬率,並且將他們的結果寫成了一本名為《投資收益百年史》(Triumph of the Optimists)的書。作者總結了美國股票報酬率沒有扭曲在全球範圍股票優於債券的這個事實。
傑里米J.西格爾(Jeremy J.Sicgel)是賓夕法尼亞大學沃頓商學院金融學教授,也是《股市長線法寶》(Long Run)和《投資者的未來》(The Future for Investors)兩本書的作者[1]。他的研究涵蓋了宏觀經濟學和貨幣政策、金融市場報酬率、長期經濟趨勢等領域。
【例12-4】計算幾何平均報酬率
計算表12-1中頭5年,即1926~1930年標準普爾500大型公司股票的幾何平均報酬率。
首先,將百分數轉化成小數,加上1,然後計算它們的乘積:

請注意,數字1.529 1,是我在最初投資1美元而在5年後所得到的金額。幾何平均報酬率計算如下
幾何平均報酬率=1.529 11/5-1=0.088 7,即8.87%
因此,在這個例子中的幾何平均報酬率大約為8.87%。這裡有一個提示:如果你使用財務計算器,你可以輸入1美元作為現值,1.529 1美元作為終值,5作為期數。然後求出未知的利率。你應該得到和我們相同的答案。
到目前為止,你可能已經注意到,在我們的示例中,幾何平均報酬率似乎更小。這個規律將一直成立(只要報酬率不完全相同,否則這兩個“平均值”將相等)。表12-4和圖12-10顯示的算術平均報酬率和幾何平均報酬率及其標準差說明了這一點。
如表12-4所示,幾何平均報酬率(四捨五入之前)均比算術平均報酬率小,但兩者的差異相差較大。因為對於波動較大的投資來說,兩者的差異更大。實際上有個近似換算的方法。假設所有的數字都用小數表示(與百分比不同),幾何平均報酬率等於算術平均報酬率減去方差的一半。例如,觀察大型公司的相關數據,算術平均值為0.120,標準差為0.199,則方差為0.040。那麼近似的幾何平均值為0.120-0.040/2=0.100,在本例中與實際值相同。
【例12-5】幾何平均值
回顧圖12-4,我們展示了91年後1美元投資的價值。現在用大型公司股票投資的價值來檢驗表12-4的幾何平均值。
在圖12-4中,大型公司的股票投資在91年間從1美元增長到了6 029.16美元。因此,幾何平均報酬率為
幾何平均報酬率=6 029.161/91-1=0.100 0,或10.0%
計算得出的10.0%如表12-4所示。為了練習,用同樣的方法檢查表12-4的其他一些數字。
表12-4 幾何平均報酬率與算術平均報酬率(1926~2016年) (%)
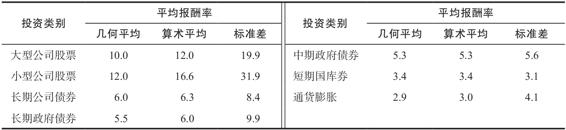
資料來源:Morningstar,2017,author calculations.
12.5.3 算術平均報酬率還是幾何平均報酬率
當我們觀察歷史報酬率時,幾何平均報酬率和算術平均報酬率之間的差異並不是很難理解。換個稍微不同的方式來說,幾何平均告訴你平均每年實際賺取了多少,每年複利一次。算術平均告訴你在典型的一年中賺取了多少,你應該用適當的答案來回答你想要問的問題。
一個有點棘手的問題是,在預測未來的財富水平時,應該採用哪一個平均報酬率,關於這一點分析師和財務規劃師有很多的困惑。首先,讓我們直接給出一個事實:如果你知道真實的算術平均報酬率,那麼這就是你應該在預測中採用的。舉例來說,如果你知道算術平均報酬率是10%,那麼你關於1 000美元的投資在10年後價值的最好猜測是將1 000美元以10%的利率投資在10年後獲得的終值,即2 593.74美元。
然而,我們面臨的問題是,我們通常只有算術平均和幾何平均的估計值,而估計值是有誤差的。在這種情況下,算術平均報酬率可能對於較長的期間而言太高了,而幾何平均報酬率可能對於較短的期間而言太低了。因此,你應該考慮利用算術平均數作為樂觀情形去計算長期的預計財富水平,而利用幾何平均數去計算短期的預計財富水平則可能是悲觀的。
幸運的是,我們可以用一種簡單的方法將兩種平均數結合起來,這種方法被稱為布盧姆公式。[2]假設我們根據N年數據已經計算出幾何和算術平均數,現在希望用這些平均數來構建T年期平均報酬的預測,即R(T)。其中,T小於N,這裡我們要做的是
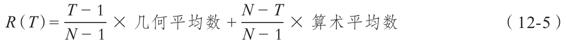
例如,根據25年的年度報酬率數據,我們計算出算術平均報酬率為12%,幾何平均報酬率為9%。按照這些平均報酬率,我們進行1年期、5年期、10年期的平均報酬率預測。這3個預測值可以計算如下
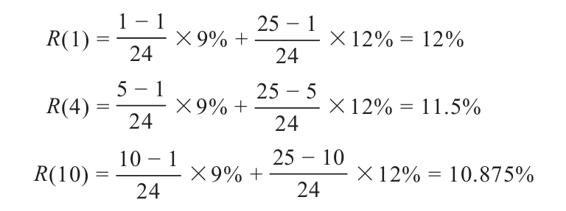
因此,我們看到1年期、5年期、10年期的預測值分別是12%、11.5%、10.875%。
實際情況是,布盧姆公式表示的是如果運用基於較長期間(如這裡我們用的是91年)而計算的平均數去預測未來的大約10年,那麼你就應該採用算術平均數。如果你要預測未來幾十年的情況(例如做退休的計劃),那麼你就應該區分算術和幾何平均數之間的差異。最後,如果出於某種原因,你正在做包含許多個10年的非常長的預測,就應該採用幾何平均數。
這裡總結了我們關於幾何平均數和算術平均數的討論。最後要注意的一點是,以後我們說“平均報酬率”的時候,除非明確說明,一般我們指的是算術平均報酬率。
概念問題
12.5a 如果你希望預測股票市場在下一年裡會怎麼樣,你應該採用算術平均數還是幾何平均數?
12.5b 如果你希望預測股票市場到下個世紀會怎麼樣,你應該採用算術平均數還是幾何平均數?
[1] 這兩本書的中文版已由機械工業出版社出版。
[2] 這個簡潔的結果來自Marshall Blume (“Unbiased Estimates of Long-Run Expected Rates of Return,” Journal of the American Statistical Association, September 1974, pp. 634–38)。