Print this chapterPrint this chapter

e1 Stephen Ross 公司理財 v12A

9.5　內部報酬率

現在我們來看看NPV最重要的替代選擇——內部報酬率（internal rate of return），即大家所熟知的IRR。正如我們即將看到的，IRR同NPV高度相關。在內部報酬率法則下，我們試圖找出一個單一的報酬率指標來概括衡量項目的特徵。另外，我們希望這個指標是某種程度上的內部指標，也就是僅僅依賴於某個特定項目的現金流量，而不受其他比率指標的影響。

為了說明IRR背後的理念，我們考慮一個投資成本為100美元，在1年後給付110美元的例子。假設有人問你，“這項投資的報酬率是多少？”你怎麼說？顯而易見，我們都會說是10%，因為對於我們支付的每1美元，我們都收回了1.1美元。實際上，正如我們即將看到的，這個項目的內部報酬率，或者說IRR，就是10%。

這個有著10%的內部報酬率的項目是不是一個好的投資呢？同樣，我們很顯然會認為如果必要報酬率小於10%，那麼這就是一個好的投資。這種直覺是正確的，它將IRR法則表示如下：

根據IRR法則，如果IRR超過了必要報酬率，那麼這個項目是可接受的；否則應拒絕。

假定我們要計算這個簡單投資項目的NPV，其貼現率為R，那麼NPV為

NPV=-100+[110/（1+R）]

現在，假設我們並不知道貼現率。這就出現了問題，但是，我們仍然可以問，貼現率需要達到多高，才會使得這個項目被拒絕。我們知道，當淨現值恰好為0時，我們接不接受這個項目並沒有什麼區別。換句話說，當NPV=0時，這個項目就處於經濟上的盈虧平衡點，既不創造價值，也不會帶來價值損失。為了找到盈虧平衡點的貼現率，我們不妨令NPV=0，求解R值

NPV=0=-100+[110/（1+R）]

100=110/（1+R）

1+R=110/100=1.1

R=0.1，或10%

這個10%就是我們所說的這項投資的報酬率。我們現在需要說明的是，內部報酬率（或者簡稱報酬率）就是使得一項投資淨現值為0時的貼現率。這是一個重要的發現，因此我們可以重述以上法則：

一項投資的IRR就是將其作為貼現率時，會使得項目淨現值為0的必要報酬率。

IRR就是淨現值為0時的貼現率，這一點很重要，因為它告訴我們如何為更加複雜的項目計算報酬率。正如我們所看到的，計算單期項目的IRR非常簡單。但是，假設我們現在考慮的是有著像圖9-4所列示現金流量的項目。如圖所示，這個項目花費成本100美元，並在其後2年有著每年60美元的現金流量，所以，它只比單期投資的例子稍微複雜一點。但是，如果有人問這個項目的報酬率是多少，你應該怎樣回答？這看起來並沒有顯而易見的答案（至少對於我們來說是如此）。然而，根據我們現在所知的，我們可以令NPV=0，從而求出貼現率

NPV=0=-100+[60/（1+IRR）]+[60/（1+IRR）2]

不幸的是，無論是手工計算還是使用計算器，一般來說尋找IRR的唯一辦法就是通過不斷的試錯。這也正是在第5章中求年金的未知報酬率和第7章中求債券到期收益率時所面臨的問題。事實上，我們現在終於明白，在以上的兩種情況中，都是在求IRR。

在本例中，現金流構成了2年期的60美元年金。想要求出IRR，我們可以嘗試一些不同的貼現率，直到找出答案。如果我們從0%開始，NPV顯然是120-100=20美元。當貼現率為10%時，我們有

NPV=-100+（60/1.1）+（60/1.12）=4.13（美元）

圖9-4　項目現金流量（單位：美元）

現在，我們更加接近答案了。我們在表9-5中列示了其他一些可能性。從這些計算中可以看出，當貼現率為10%～15%之間的某個數時，NPV等於0，所以IRR在這個範圍內。再花費些精力，我們可以求出IRR為13.1%。[1]所以，如果我們的必要報酬率小於13.1%，我們應該接受這個項目；相反，如果我們的必要報酬率大於13.1%，我們應該拒絕這個項目。

表9-5　不同貼現率下的NPV

至此，你應該可以發現IRR法則和NPV法則十分相似。實際上，有時候內部報酬率（IRR）就叫作貼現現金流量（DCF）報酬率。說明NPV和IRR之間關係的最簡單的方法就是根據表9-5中的數據畫出圖形。我們令y軸（縱軸）代表NPV，x軸（橫軸）代表貼現率（或者相反）。如果擁有大量的數據，我們就能得到一條光滑的曲線，稱為淨現值曲線（net present value profile）。圖9-5列示了該項目的淨現值曲線。從貼現率為0開始，我們最初可在y軸上得到淨現值為20美元的點。隨著貼現率的增加，NPV平穩下降。那麼該曲線在何處與x軸相交？當淨現值為0時，也就是IRR為13.1%時，才會出現這種情形。

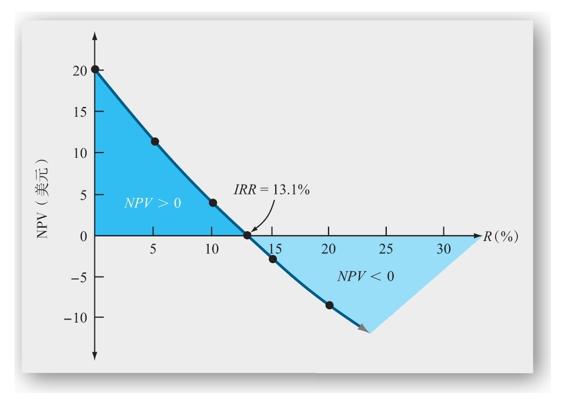
圖9-5　NPV曲線

在我們的例子中，採取NPV法則和IRR法則能帶來一致的取捨決策結果。如果必要報酬率小於13.1%，那麼根據IRR法則，我們會接受項目。如圖9-5所示，在任何小於13.1%的貼現率下，淨現值都為正，那麼根據NPV法則，我們也會接受這個項目。在本例中，兩種法則給出了同樣的答案。

【例9-4】IRR計算

一個項目前期啟動費用為435.44美元，前3年的現金流量分別為100美元、200美元和300美元。IRR是多少？如果必要報酬率是18%，我們是否應該接受這個項目？

我們將要描繪出NPV曲線，並且通過計算不同貼現率下的NPV來求IRR。你應該練習一下，檢查我們的答案。從貼現率為0開始，我們可得：

當貼現率為15%時，NPV等於0，所以IRR為15%。如果必要報酬率為18%，那麼不應該接受這個項目。原因是在18%的貼現率下，NPV為負（經驗證為-24.47美元）。在本例中，IRR法則給出的結論是一致的。我們不應該接受這個項目，因為15%的報酬率小於18%的必要報酬率。

此時，你可能會想IRR法則和NPV法則得出的結論是否總是一致的。實際上，只要滿足兩個重要的條件，那麼答案是肯定的。第一，項目的現金流量必須是符合常規的，也就是說第一筆現金流量（初始投資）應該是負的，而其餘的所有現金流量都是正的。第二，項目應該是獨立的，也就是接受或者拒絕該項目的決策不應該影響到接受或者拒絕其他項目。第一個條件通常會被滿足，但是第二個條件常常不能得到滿足。無論在什麼情況下，當其中一個或者兩個條件都不滿足時，就會產生問題。我們在下面討論這類情況。

使用電子表格　用電子表格計算內部報酬率

因為手工計算太過複雜，財務計算器，特別是電子表格常常被用於計算IRR。各種財務計算器的計算步驟不勝枚舉，所以我們僅關注電子表格的計算過程（財務計算器的計算過程在附錄D中說明）。正如下面例子所說明的，電子表格的使用非常簡易。

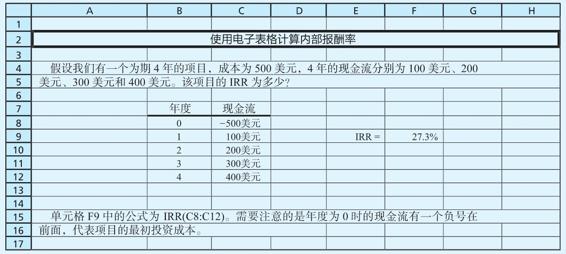
資料來源：Microsoft Excel.

9.5.1　IRR的問題

當現金流量並非常規，或者我們試著去比較兩個或兩個以上的項目哪一個更好的時候，IRR的使用會帶來一定的問題。令人驚奇的是，在第1種情況下，“報酬率是多少”這個簡單的問題變得難以回答。在第2種情況下，IRR可能錯誤地引導我們。

1.非常規現金流量

假設我們有一個採礦項目，需要60美元的投資。第1年的現金流量是155美元，第2年礦產被採盡，但是我們還需要花費100美元來修整礦區。如圖9-6所示，第1年和第3年的現金流量都為負。

圖9-6　項目現金流（單位：美元）

為求出這個項目的IRR，我們計算不同貼現率下的NPV。

這裡的淨現值似乎表現得有所與眾不同。首先，當貼現率從0%增加到30%時，淨現值一開始為負值，然後變為正值。這似乎與正常的情況相反，因為淨現值隨著貼現率的增長而增長了。而後，淨現值開始變小，再次成為負值。那麼，IRR究竟是多少呢？為了找出答案，我們在圖9-7中畫出NPV曲線。

在圖9-7中，可以觀察到當貼現率為25%時NPV為0，所以25%就是IRR，它真的是嗎？當貼現率為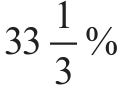時，NPV同樣等於0。哪一個是正確的？答案是兩者都是，或者兩者都不是；更確切地說，這沒有一個明確的答案。這是一個多重報酬率（multiple rates of return）問題。許多財務計算機軟件（包括一種應用於個人計算機的暢銷軟件）都沒有意識到這個問題，只報告了求出的第一個IRR。而其他軟件只報告最小的正IRR，儘管這個答案並不比其他任何一個更好。

在當前的例子中，IRR法則已經完全不適用了。假設我們的必要報酬率是10%，那麼我們是否應該接受這個項目呢？例子中的兩個IRR都大於10%，所以，根據IRR法則，也許我們應該接受。但是，根據圖9-7所示，當貼現率小於25%時，NPV為負，即這不是一個好的投資項目。那麼在什麼情況下應該接受這個項目呢？回過頭來最後再看一次圖9-7，可以發現只有當必要報酬率在25%和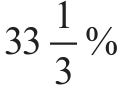之間時，淨現值才為正。

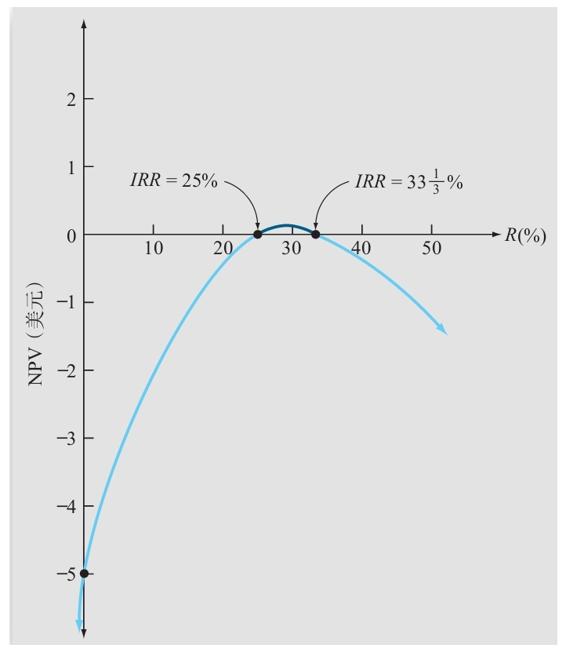
圖9-7　NPV曲線

非常規現金流量在很多情況下都會發生。例如，1995年11月，康涅狄格州米爾斯通（Millstones）核電站的所有者東北設備（Northeast Utilities）不得不關閉電站裡的三個反應堆。這三個反應堆預計在1997年1月才能恢復使用。根據某種估計，關閉的成本大約為3.34億美元。實際上，所有的核電站最終都將關閉，由此帶來的解除核電站運行的成本相當巨大，造成了項目結束時鉅額的負現金流量。德國運營核電站的4家公司已經撥出450億美元用於該國的核電站關閉。

故事的教訓就是當現金流量為非常規時，IRR可能會顯得奇怪。但這並不是什麼好擔心的事，因為NPV法則是一直適用的。這說明了一件奇怪的事“報酬率是多少”這個明顯的問題，並不總是有一個好的答案。

【例9-5】IRR是多少

你正在考慮一個投資項目，這個項目需要在今天投入51美元。1年後你將得到100美元，但同時你又必須在2年後支付50美元。那麼這個項目的IRR是多少？

你現在已經警覺到這是一個非常規現金流量的問題，所以當你看到IRR不止一個的時候，大概就不會覺得驚奇。如果你開始使用試錯法來求IRR，那麼你可能要花費很長時間。因為這個項目根本就不存在IRR。在所有的貼現率下NPV都是負值，所以在任何情況下我們都不應該接受這個項目。那麼這個項目的報酬率究竟是多少呢？我們和你一樣一無所知。

【例9-6】“我思，故我知將會有多少個IRR”

我們已經知道IRR的個數可能會超過一個。如何你想要確定已經找到了全部可能的IRR，那麼應該怎麼做？答案來自於偉大的數學家、哲學家和財務分析師笛卡爾（他提出“我思，故我在”的名言）。笛卡爾的符號法則說明IRR的最多可能個數等於現金流量從正值變為負值和/或由負值變為正值的次數。[2]

在前面IRR為25%和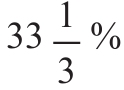的例子中，是否還有其他的IRR呢？現金流量由正值變為負值，再變回正值，符號總共發生兩次變化。因此，根據笛卡爾法則，IRR的最多個數為兩個，我們不用再去找其他的IRR。需要注意的是，IRR的數量可能少於最多可能個數（見例9-5）。

2.互斥投資

即使只有一個IRR，也可能會產生另外一個問題，那就是互斥投資決策（mutually exclusive investment decision）問題。如果有X和Y兩個投資項目，是互斥的，也就是說如果我們接受了其中一個項目就不能再接受另外一個項目。如果兩個項目不是互斥的，我們就說它們是相互獨立的。例如，如果我們有一小塊地，那麼可以建一個加油站或者一棟公寓樓，但是不能兩樣都建，這就是一個互斥選擇。

到目前為止，我們關注的焦點在於給定的投資項目是否值得進行。但是常常會出現另一個相關的問題：給定兩個或者多個相互排斥的項目，哪一個是最好的？答案很簡單，有著最大NPV的那一個。我們能不能說，最好的是有著最高報酬率的那一個？就像我們下面將要展示的那樣，答案是否定的。

為了說明IRR法則和互斥投資的問題，我們考察下面兩個互斥投資項目的現金流量。

A投資的IRR是24%，B投資的IRR是21%。因為這些投資項目是互斥的，我們只能接受其中一個。簡單從直覺出發，我們認為A投資更好，因為它有著更高的報酬率。不幸的是，直覺並非總是正確的。

為了說明為何A投資並不一定是兩個項目中更好的那一個，我們計算這兩個投資項目在不同貼現率下的NPV。

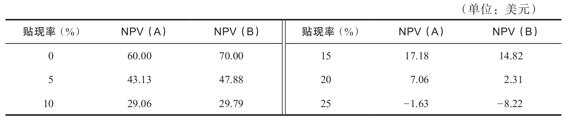
A投資的IRR（24%）大於B投資的IRR（21%）。但是，如果比較兩者的NPV，你會發現，哪個投資項目的NPV更高則取決於我們的必要報酬率。B投資的總現金流量更大，但是它收回成本的速度比A投資慢。其結果是，當貼現率較低時，B投資有著更高的NPV。

在我們的例子中，根據NPV或IRR進行的排序在某些貼現率水平下是相互衝突的。例如，當我們的必要報酬率是10%時，B投資的NPV更高，所以儘管此時A投資有著更高的報酬率，B投資仍然是兩者中更好的那一個。如果我們的必要報酬率是15%，那麼就沒有衝突，A投資是更好的。

NPV和IRR在互斥投資中的衝突可以用NPV曲線來說明，如圖9-8所示。從圖9-8中，我們可以發現兩條NPV曲線在貼現率大約為11.1%時相交。同時注意到，貼現率小於11.1%時，B投資的NPV較大。在這個範圍內，接受B投資給我們帶來的收益更大，儘管A投資的IRR更高。當貼現率大於11.1%時，A投資的NPV則更大。

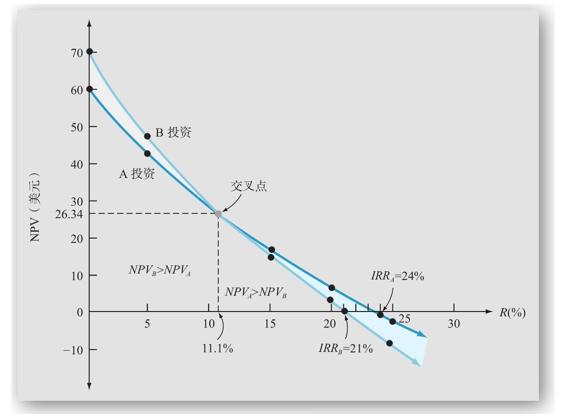
圖9-8　互斥項目的NPV曲線

這個例子說明，當我們遇到互斥項目時，不能根據它們的報酬率進行排序。更一般地說，在任何時候，只要我們以IRR作為評價項目好壞的標準時，就可能產生誤導。我們必須觀察相對應的NPV，來避免做出錯誤的選擇。記住，我們最終關注的是為股東創造價值，所以無論報酬率相對是多少，總是偏向那些有著更高NPV的項目。

如果聽起來與直覺不符，你可以這樣想。假設你有兩個投資項目，其中一個的報酬率為10%，並且能使你馬上增加100美元的財富。另外一個的報酬率為20%，能使你馬上增加50美元的財富。你更喜歡哪一個？我們更加喜歡100美元而不是50美元，不管報酬率是多少，所以我們更喜歡第一個。

【例9-7】交叉點報酬率計算

在圖9-8中，NPV曲線在貼現率大約為11%時相交。我們應該如何確定這個交叉點具體是多少？交叉點比率，從定義上而言，指的是使得兩個項目的NPV相等的貼現率。為了說明這一點，假設我們有兩個互斥的投資項目如下表所示。

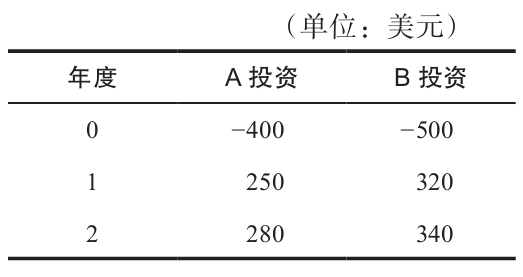
交叉點比率是多少？

為了找出交叉點，首先考慮用B投資來代替A投資的情況。如果進行了替換，你需要額外投資100（=500-400）美元。對於這100美元的投資，你在第1年可額外獲得70（=320-250）美元，第2年可額外獲得60（=340-280）美元。這是不是一個好的替代方案？換句話說，是否值得投資這額外的100美元？

根據我們的討論，項目轉換產生的NPV，即NPV（B-A）為

NPV（B-A）=-100+[70/（1+R）]+[60/（1+R）2]

我們不妨令NPV=0，求出此時的報酬率，即IRR。

NPV（B-A）=0=-100+[70/（1+IRR）]+[60/（1+IRR）2]

如果完成計算，你會發現IRR剛好等於20%。這說明當貼現率為20%時，兩個項目對我們而言並沒有區別，因為兩者現金流量差異的NPV等於0。其結果是兩個投資項目有著同樣的價值，所以交叉點比率就是20%。檢查一下可以發現，當貼現率為20%時，兩個項目的NPV都為2.78美元。

總而言之，你可以找出兩者現金流量的差異並利用差異算出IRR，從而找出交叉點比率。至於用哪個減哪個，並沒有關係。為了說明這一點，你可以試著去找出以A投資替換B投資的IRR（A-B），將得出同樣的結果。同樣，可以練習一下，試著去找出圖9-8中交叉點比率的精確值。（提示：是11.070 4%。）

3.投資還是融資

考慮如下表所示兩個獨立的投資項目。

公司在最初為A項目支付現金，而B項目則給公司帶來現金。雖然大部分投資項目都與A類似，但是類似B的情況也時有發生。例如，考慮一家公司舉辦研討會的情況，與會者往往提前交納會費。因為大部分的開支通常花費在研討會期間，所以現金流入早於現金流出。

對於這樣兩個項目，假設必要報酬率都是12%，根據IRR法則，我們應該選擇哪個項目？如果計算IRR，你會發現兩個項目都是30%。

根據IRR法則，兩個方案我們都應該接受。但是如果我們在12%的貼現率下計算B項目的NPV，我們可得

100-130/1.12=-16.07（美元）

在這個例子中，IRR法則和NPV法則得出的結論並不一致。為了說明具體情況，圖9-9展示了每個項目的NPV曲線。正如你所看到的，B項目的NPV曲線是向上傾斜的。因此，如果必要報酬率大於30%，B項目應該被接受。

當某個方案有著類似B項目的現金流量時，IRR是你對外支付的利率，而不是收到的利率。正因為如此，我們說B項目有著融資型現金流量，A項目有著投資型現金流量。當且僅當你有一個費用低廉的資金來源時，才能夠接受那些有著融資型現金流量的項目，這意味著項目的IRR需要低於必要報酬率。

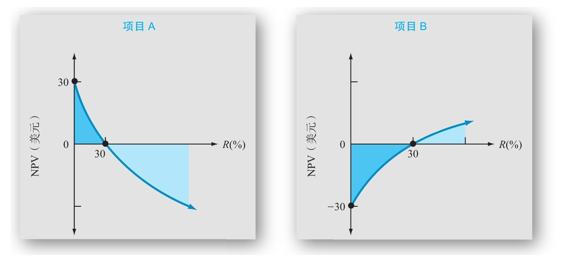
圖9-9　投資和融資的NPV曲線

9.5.2　IRR的可取之處

儘管有著各種缺點，IRR在實務中卻非常通用——甚至比NPV還廣泛。這可能是因為它滿足了一些NPV所不能滿足的需求。在進行投資分析時，人們似乎更加喜歡談論報酬率而不是貨幣的絕對數額，特別是財務分析師。

同樣，IRR還提供了一個交流有關方案的意見的簡單途徑。一個經理可能會對另外一個經理說：“重建行政署的報酬率為20%。”這聽起來多少要比“在10%的貼現率下，淨現值為4 000美元”顯得簡單。

最後，在特定的環境下，IRR可能比NPV更具有實踐上的優點。如果不能獲得合適的貼現率，我們就無法估計NPV，但是仍然可以估計出IRR。假設我們並不知道一個項目的必要報酬率，但是它有著，例如，40%的報酬率，我們可能傾向於接受這個項目，因為必要報酬率比這個還要高的可能性非常小。IRR的優點和缺點總結如下。

內部報酬率法則的優點和缺點

9.5.3　修正的內部報酬率

為了解決標準IRR可能造成的一些問題，人們常常建議使用修正的IRR。下面我們將會看到使用幾種不同的方法來計算修正的IRR（MIRR），但它們根本的思想都是先修正現金流量，然後根據修正後的現金流量計算IRR。

舉例說明，讓我們回顧一下圖9-6中的現金流量：-60美元，155美元，-100美元。正如我們看到的，有兩個IRR，分別為25%和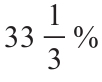。接下來我們要說明3種不同的MIRR，它們都擁有同樣的特性，那就是隻能得出一個答案，從而消除了多重IRR的問題。

1.方法1：貼現法

貼現法的思路是將所有負的現金流量用必要報酬率貼現，轉化為現值並同初始成本相加，然後再計算IRR。因為只有第一筆修正現金流量為負值，所以只能得出一個IRR。這裡的貼現率可以是必要報酬率，也可以是其他外部提供的利率。我們將用的是項目的必要報酬率。

如果項目的必要報酬率是20%，則修正的現金流量應該是這樣的

時間0：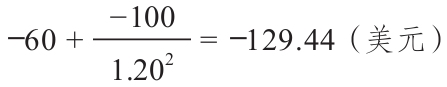

時間1：+155（美元）

時間2：0（美元）

如果現在你計算MIRR，可以得到答案為19.74%。

2.方法2：再投資法

在再投資法下，我們把除了第一筆之外的所有現金流量（正的和負的）累積計算複利直到項目的末期，然後再計算IRR。從某種程度上，我們是把現金流量進行再投資直到項目結束，中途並未抽取出來。所使用的利率可以是項目的必要報酬率，也可以是單獨確定的“再投資利率”。我們將要用的是必要報酬率。下面是我們計算的修正現金流量

時間0：-60（美元）

時間1：0

時間2：-100+（155×1.2）=86（美元）

根據這些現金流量求出的MIRR為19.72%，比我們用貼現法計算得到的結果要稍微小一些。

3.方法3：綜合法

顧名思義，綜合法就是將前面兩種方法綜合。將負的現金流量貼現得到現值，將正的現金流量以複利計算到項目末期。在實際操作中，可能使用不同的貼現率和複利利率，但在此我們將繼續使用項目的必要報酬率。

在綜合法下，修正的現金流量計算如下

時間0：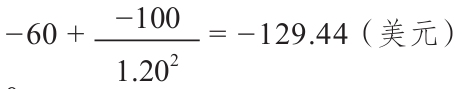

時間1：0

時間2：155×1.2=186（美元）

看看你是否同意MIRR是19.87%——這是3種方法中最高的。

4.MIRR還是IRR：哪一個更好

MIRR具有爭議性。一方面，有人宣稱MIRR要優於IRR。例如，通過合理的設計就可以避免多個內部報酬率的問題。

另一方面，批評者認為MIRR代表了“毫無意義的內部報酬率”。正如我們的例子所表明的那樣，MIRR的問題之一在於計算方法的多樣性，而且也沒有明確的理由說明三者中哪個最好。對於例子中簡單的現金流量，三種方法計算所得的結果相差不大，但是面對複雜的項目，結果可能差距很大。再者，我們難以明確地解釋和說明MIRR。它看起來像報酬率，但是它是根據修正後的現金流量計算出來的報酬率，而不是根據項目實際的現金流計算出來的。

我們並不會偏袒哪一邊。但是，需要注意到計算MIRR時需要貼現，計算複利，或者兩者都要——這帶來兩個明顯的問題。第一，如果我們有了相關的貼現率，為什麼不直接算出NPV。第二，因為MIRR的計算需要依靠一個外部提供的貼現（或者說複利）率，所以你得到的答案並不是真正的“內部”報酬率，因為根據定義，內部報酬率的計算僅僅依據項目的現金流量。

我們將繼續堅持遇到這一類問題時的處理原則。一個項目的價值並不取決於公司如何使用該項目產生的現金流量。公司可能會用項目產生的現金流量來資助其他項目、支付股利或者為高管購買噴氣式飛機，這並不重要，因為未來現金流的使用並不影響項目當前的價值。因此，一般來說沒有必要考慮將項目進行中產生的現金流再投資的情況。

概念問題

9.5a　在哪些情況下，IRR法則和NPV法則所得到的取捨決策是相同的？在哪些情況下它們的結果是相互衝突的？

9.5b　IRR法則優於NPV法則的其中一點是使用IRR法則時不必知道項目的必要報酬率，一般來說，這種說法是否正確？

[1] 再花費些精力（或者使用個人計算機），我們可以發現IRR近似13.066 238 629%（取9位小數）—沒有人會希望有這麼多的小數位數！

[2] 更加準確地說，大於-100%的IRR個數等於現金流量符號的變化次數，或者它與符號變化次數之差會是個偶數。例如，如果有5次符號變化，那麼可能有5個IRR，或者3個、1個。如果是2次符號變化，那麼可能有2個IRR或者沒有IRR。