e1 Stephen Ross 公司理財 v12A
7.6 通貨膨脹和利率
到現在為止,在討論利率、收益率和報酬率時,我們都沒有考慮到通貨膨脹的影響。因為通貨膨脹是一個重要的因素,所以我們接下來看看通貨膨脹的影響。
7.6.1 實際利率和名義利率
在考察利率或其他金融市場上的貼現率、債券收益率、報酬率和必要報酬率時,通常我們都必須區分實際利率(real rate)和名義利率(nominal rate)。名義利率是指未經過通貨膨脹調整的利率,實際利率是經過通貨膨脹調整的利率。
為了考察通貨膨脹的影響,假定目前物價每年上漲5%。換句話說,通貨膨脹率是5%。有一項1年後價值115.50美元的投資。它目前的成本是100美元。因為現值是100美元,1年後的終值是115.50美元。因此,這項投資的報酬率是15.5%。然而,在計算15.5%的報酬時,我們並沒有考慮通貨膨脹的影響,因此這是名義報酬率。
通貨膨脹在這裡有什麼影響呢?為了回答這個問題,我們假定比薩年初價格是每個5美元。那麼,我們有100美元就可以買20個比薩。因為通貨膨脹率是5%,在年末的時候,比薩的價格將上漲5%,換句話說,比薩在年末的價格為5.25美元。如果我們進行這項投資,那麼,年末時我們能買幾個比薩呢?以比薩來計量,我們的報酬率又是多少呢?
從我們的投資所得到的115.50美元可以買115.50/5.25=22個比薩。比20個比薩還要多,所以我們的比薩報酬率是10%。這個例子可以告訴我們,即使我們投資的名義報酬率是15.5%,通貨膨脹使得購買力只上升了10%。換句話說,實際上我們的富有程度比起過去只增加了10%。因此,實際報酬率是10%。
或者,我們也可以說,在5%的通貨膨脹率下,我們所得到的每一筆115.50美元的名義收入實際上少了5%。因此,1年後我們的投資的實際價值是
115.50/1.05=110(美元)
這裡,我們所做的就是將115.50美元貶值5%。因為我們放棄了100美元的當前購買力以換取相同購買力的110美元,我們的實際報酬率是10%。因為這裡已經剔除了通貨膨脹的影響,因此110美元是以目前金額來計量的。
實際利率和名義利率的區別非常重要,值得再重複一遍:
一項投資的名義利率是你所擁有的錢的變動百分比。
一項投資的實際利率就是你的錢所能購買數量的變動百分比,也就是購買力的變動百分比。
7.6.2 費雪效應
前面所討論的實際報酬率和名義報酬率之間的關係叫作費雪效應(Fisher effect,以偉大的經濟學家歐文·費雪(Irving Fisher)的名字命名)。因為投資者最終考慮的是他的錢能買到什麼,因此,他們會要求針對通貨膨脹的補償。用R代表名義利率,r代表實際利率。費雪效應告訴我們,實際利率、名義利率和通貨膨脹之間的關係可以表述為
1+R=(1+r)×(1+h) (7-2)
式中,h是通貨膨脹率。
在上面的例子中,名義利率是15.50%,通貨膨脹率為5%,那麼,實際利率是多少?只要將數字代入,就可以得出答案
1+0.155 0=(1+r)×(1+0.50)
1+r=1.155 0/1.05=1.10
r=10%
這個利率和我們前面所求得的一樣。如果換個角度看費雪效應,我們可以重新做如下整理
1+R=(1+r)×(1+h)
R=r+h+r×h (7-3)
它告訴我們名義報酬率包括3部分:第1部分是投資所得到的實際報酬,r;第2部分是對原本投資的錢因通貨膨脹(h)所導致價值損失而做出的補償,h;第3部分則代表對這項投資所賺取的錢的補償,因為它們實際上也因通貨膨脹而貶值了。
第3部分通常非常小,因而經常被省略。這樣,名義利率約等於實際利率加上通貨膨脹率。
R≈r+h (7-4)
應該重點注意的是,財務上使用的比率,如利率、貼現率和報酬率等,幾乎都是名義上的。為了提醒你這一點,在以下的大部分討論中,我們將用R而不是r,來表示這些比率。
【例7-5】費雪效應
如果投資者要求10%的實際報酬率,而且通貨膨脹率是8%,那麼名義報酬率近似等於多少?精確的名義報酬率又是多少?
首先,名義報酬率近似等於實際報酬率加上通貨膨脹率:10%+8%=18%。根據費雪效應,我們可以得到
1+R=(1+r)×(1+h)=1.10×1.08=1.188 0
因此,精確的名義報酬率非常接近於19%。
7.6.3 通貨膨脹與現值
一個經常出現的問題就是通貨膨脹對現值計算的影響。回答這一問題的基本原則很簡單:用名義利率貼現名義現金流量,用實際利率貼現實際現金流量。只要保持一致性,那麼所得結果就相同。
例如,假設今後的3年中你每年都要從銀行取錢,而且你希望每次所取的錢的購買力維持在目前幣值水平下的25 000美元。如果年通貨膨脹率為4%,那麼每年所取錢數只需簡單增加4%即可補償通貨膨脹的影響。這樣,每年取錢數為
C1=25 000×1.04=26 000(美元)
C2=25 000×1.042=27 040(美元)
C3=25 000×1.043=28 121.60(美元)
如果採取適當的名義貼現率10%,那麼這些現金流量的現值為多少?按標準計算方法,答案為
PV=(26 000/1.10)+(27 040/1.102)+(28 121.60/1.103)
=67 111.65(美元)
請注意,這裡我們用名義利率貼現名義現金流。
如果要用實際現金流來計算現值,那麼就要採用實際利率進行貼現。按照費雪等式,實際利率r計算如下
1+R=(1+r)×(1+h)
1+0.10=(1+r)×(1+0.04)
r=0.057 7
按照計劃,每年的實際現金流為25 000美元的年金。這樣,按照實際利率計算的現值可以計算如下
PV=25 000×[1-(1/1.057 73)]/0.057 7
=67 111.65(美元)
因此,我們得到的結果與前面的結果完全相同(採用實際利率時允許有四捨五入方面的小差異)。當然,我們也可以採用上一章所介紹的增長型年金公式。這裡,所取錢數以每年4%的速度增長,採用增長型年金公式時其現值為
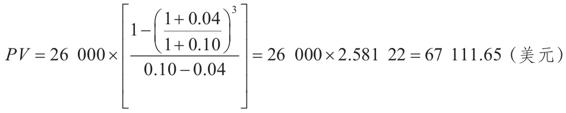
所得結果與前面的計算結果完全相同。
概念問題
7.6a 名義報酬率和實際報酬率有什麼差異?對於一個典型的投資者來說,哪一種更加重要?
7.6b 什麼是費雪效應?