e1 Stephen Ross 公司理財 v12A
7.1 債券和債券估值
當公司和政府希望從公眾處獲得長期借款時,常常通過發行或者售賣債務證券,即債券。在本部分,我們將介紹公司債券的諸多特徵和與債券有關的術語。我們接下來會討論與債券有關的現金流量,以及我們是如何運用貼現現金流量的方法對債券進行估值的。
7.1.1 債券特徵與價格
就像我們在前面章節提到的一樣,債券通常是一項純利息貸款,意即借款人在每個期間只還利息,而本金只有等借款到期日才會進行清償。舉個例子,假設貝克公司(Beck Corporation)準備借入1 000美元,期限30年。相似公司類似債券的利率為12%。因此,在這30年中,貝克公司每年要償還的利息額為0.12×1 000美元=120美元。在第30年年底,貝克公司將會清償1 000美元。正如例子所示,債券是一種非常簡單的融資安排。但實際上,與債券相關的專業術語卻十分豐富,因此我們以這個例子來定義一些非常重要的術語。
在上述例子中,120美元的定期利息支付被稱為債券的票面利息(coupon)。由於票面利息是固定的,而且每年支付,因此這種類型的債券有時也被稱為等息債券。而在借款期末被清償的數額被稱為債券的面值(face value),或是面額(par value)。正如我們例子所說的,公司債券的面值通常為1 000美元,而且一份以面值出售的債券就被稱為平價債券。政府債券的面值通常要大得多。最後,每年的利息除以面值就被稱為債券的票面利率(coupon rate)。由於120美元/1 000美元=12%,因此貝克債券的票面利率為12%。
距離面值清償的年數被稱為債券的到期日(maturity)。公司債券在初始發行時所設定的到期日通常為30年,但這也會發生變化。一旦債券發行後,距到期日的年數就會隨著時間的流逝而降低。
7.1.2 債券價值和收益率
隨著時間的流逝,市場上的利率會發生變化,而與債券有關的現金流保持不變。因此,債券的價值會發生浮動。當利率上升時,債券中仍未清償的現金流量的現值將會降低,債券將變得不像原來那麼值錢;當利率下降時,債券將會變得更有價值。
為了確定債券在特定時點的價值,我們需要知道距到期日的期數、面值、利息以及具有類似特徵的債券的收益率。市場上對於一份債券所要求的利率被稱為債券的到期收益率(yield to maturity,YTM),這項利率有時也被簡稱為債券的收益率。在給定了這些信息後,我們可以計算出現金流量的現值,作為債券當前市場價值的估計值。
假定Xanth公司曾準備發行一份到期期限為10年的債券。Xanth債券每年的票面利息為80美元。類似債券的到期收益率為8%。基於我們前面的討論,Xanth債券在未來的10年,每年支付的票面利息都為80美元。而且,在10年後,Xanth公司將要向債券的持有人支付1 000美元。債券的現金流如圖7-1所示,那麼這份債券該以怎樣的價格出售呢?
如圖7-1所示,Xanth債券的現金流包括年金的部分(每年的利息)和總額部分(到期日所支付的面值)。若需估計出這份債券的市場價值,就要分別計算出這兩部分的現值,並將結果相加。
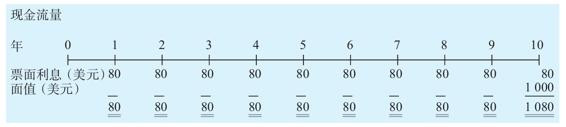
圖7-1 Xanth公司債券的現金流
注:如圖所示,Xanth公司債券有80美元的年利息和在10年後到期的價值1 000美元的面值。
首先,當利率為8%時,10年後支付的1 000美元的現值為
現值=1 000/1.0810=1 000/2.158 9=463.19(美元)
其次,在10年期間,這份債券每年支付80美元;這一系列年金流的現值為
年金現值=80×(1-(1/1.0810))/0.08
=80×(1-(1/2.158 9))/0.08
=80×6.710 1=536.81(美元)
現在我們可以將兩部分相加得到債券的價值
債券的總價值=463.19+536.81=1 000(美元)
這份債券恰好以其面值出售。這並不是一個巧合,因為市場上的現行利率為8%。如果將其當作一份純利息貸款,那麼這份債券的利率應該是多少呢?票面利息是80美元,因此這份債券只有當其售出價格為1 000美元時,利率才會恰好是8%。
為了說明當利率改變的時候會發生什麼,假定已經過去了1年。Xanth債券離到期日還有9年的時間。如果市場上的利率已經升至10%,那麼該債券的價值又會變為多少?要得到這個結果,我們將重複之前的現值計算,只是現在要用9年代替原先的10年,並用10%的收益率代替原先的8%。首先,9年後支付的1 000美元按照利率10%貼現的現值為
現值=1 000/1.109=1 000/2.357 9=424.10(美元)
其次,在剩下的9年時間中,債券每年所支付的利息仍為80美元;而在10%的利率下這一系列年金流的現值等於
年金現值=80×(1-(1/1.109))/0.10
=80×(1-(1/2.357 9))/0.10
=80×5.759 0=460.72(美元)
我們現在將兩部分的價值相加得出債券的總價值
債券總價值=424.10+460.72=884.82(美元)
因此,債券的賣出價應該為885美元。說得更直白一點,若將這份票面利率為8%的債券定價為885美元,可獲得10%的收益率。
Xanth公司債券現在出售的價格低於其面值1 000美元。為什麼?因為市場利率是10%。若將其當作一份1 000美元的純利息貸款,這份債券僅按其8%的票面利率進行支付。由於債券所支付的利率低於市場現行利率,那麼投資者願意借出的錢就會比所承諾的清償金額1 000美元要稍微少一點。由於債券是以低於面值的價格售出的,因而它被稱為折價債券(discount bond)。
使得收益率達到10%的唯一方法就是將價格降到1 000美元以下以使購買者在實際上可以從中獲得隱含利得。以Xanth公司債券為例,885美元的價格比其面值低了115美元,因此對於購買該債券並持有的投資者來說,他可以在每年獲得80美元的利息收入,還可以在債券到期日獲得115美元的利得。這份利得可以對借款人承受的低於市場利率的票面利率進行補償。
另一種幫助理解該債券被折價了115美元的方法是,注意在目前的市場狀況下,原先發行的債券每月支付的80美元利息比新發行的平價債券的利息要低20美元。而且只有當其年利息為100美元時,這份債券的價值才是1 000美元。從某種意義上來講,購買並持有Xanth公司債券的投資者在接下來的9年中每年放棄的利息額為20美元。當利率為10%時,這一系列年金流的價值為
年金現值=20×(1-(1/1.109))/0.10=20×5.759 0=115.18(美元)
這恰好就是折價的數額。
如果利率是降低2%,而非上升2%,那麼Xanth公司債券又會以怎樣的價格賣出?正如你可能猜出的,這份債券將以高於1 000美元的價格賣出。這樣的債券被稱為溢價賣出或稱為溢價債券。
這個例子與折價債券正好相反。Xanth公司債券現在是一份票面利率為8%的債券,而當前的市場利率僅為6%。投資者因而願意額外支付一定的價格來獲得這部分增加的票面利息。在這個例子中,相關的貼現率為6%,而據到期日還有9年。1 000美元面值的現值為
現值=1 000/1.069=1 000/1.689 5=591.90(美元)
票面利息流的現值為
年金現值=80×(1-(1/1.069))/0.06
=80×(1-(1/1.689 5))/0.06
=80×6.801 7=544.14(美元)
我們將兩部分的價值相加以獲得債券的價值
債券的總價值=591.90+544.14=1 136.03(美元)
因此債券總價值超出面值的部分為136美元。如果注意到票面利息在當前的市場條件下偏高20美元,我們就可以由此驗算該部分超出的價值。當利率為6%時,9年中每年帶來20美元的年金流現值為
年金現值=20×(1-(1/1.069))/0.06=20×6.801 7=136.03(美元)
這和我們剛才計算的結果一致。
基於上述例子,我們現在可以寫出債券價值的通用表達方式。如果一份債券①在到期日時支付的面值為F,②每期支付票面利息C,③到期期數為t,④每期收益率為r,那麼它的價值為
債券價值=C×[1-1/(1+r)t]/r+F/(1+r)t (7-1)
債券價值=票面利息的現值+面值的現值
【例7-1】半年期利息
在實務中,美國發行的債券通常一年支付兩次利息。因此,如果一份普通債券擁有14%的票面利率,那麼該債券的持有者每年收到的利息總額就為140美元,但這份140美元的利息將以每次70美元分兩次來支付。假設我們現在就是分析這樣一種債券,債券的到期收益率為16%。
債券的收益率都是以年利率(APR)來報價,報告的利率等於每期實際利率乘以期數。因此,若當收益率報告為16%,且半年支付一次利息,那麼實際的收益率就為每6個月8%。如果債券在7年後到期,其價格會是多少?這份債券的實際年收益率為多少?
基於之前的討論,我們知道這份債券將會折價售出,由於它的票面利率為每6個月7%,而市場所要求的收益率為每6個月8%。因此,如果我們的答案高於1 000美元,那麼我們一定錯了。
為了得到確切的價格,我們首先要計算在7年後償付的面值1 000美元的現值。如果把每6個月看作一期,那麼7年就可以看作14期。每期的貼現率為8%,那麼價值就為
現值=1 000/1.0814=1 000/2.937 2=340.46(美元)
利息可以看作14期,每期支付額為70美元的年金現值。在8%的貼現率下,這樣的年金現值為
年金現值=70×(1-(1/1.0814))/0.08
=70×(1-(0.340 5))/0.08
=70×8.244 2=577.10(美元)
總的現值就是債券的售出價格
總現值=340.46+577.10=917.56(美元)
為了計算這份債券的實際年利率,我們注意到每6個月8%的利率等同於
實際年利率=(1+0.08)2-1=16.64%
因此債券的實際年收益率為16.64%。
正如我們在本部分闡述的那樣,債券價格和利率變動的方向總是相反的。當利率上升,債券的價格就像其他任何現值一樣會下降。同樣,當利率下降,債券的價格會上升。即使借款人確定能夠全部清償,購入一份債券仍然存在風險。我們接下來對此進行討論。
7.1.3 利率風險
對於債券的持有者來說,利率的浮動所帶來的風險稱為利率風險。債券的利率風險的大小取決於債券的價格對於利率變動的敏感程度。這種敏感程度直接取決於兩個條件:距到期日的時間以及票面利率。我們接下來馬上會看到,在評估債券的時候,你應時刻記住以下的兩點。
(1)在其他條件都相同的情況下,距到期日的時間越長,利率風險越大。
(2)在其他條件都相同的情況下,票面利率越低,利率風險越大。
我們將會在圖7-2中闡述這兩點中的第1點。如圖所示,我們計算並在圖中標註了票面利率均為10%,而到期時間分別為1年和30年的兩種債券在不同的利率條件下的價格。我們注意到30年期債券價格曲線的斜率較之1年期更為陡峭。這種陡峭程度告訴我們,利率中相對較小的變動都將導致債券價值的大幅變動。相比之下,1年期債券的價格對於利率變動不敏感。
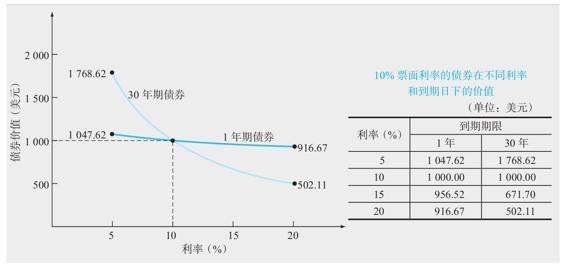
圖7-2 利率風險和到期期限
直觀上說,長期債券有較大的利率敏感度,因為其價值的一大部分來自1 000美元的面值。如果該面值的金額能夠在1年內收回,那麼利率上微小的變動就不會大幅影響這部分金額的現值。但是,一旦是按30年進行復利計息,那麼即使是利率中極小的變動,也可能對現值產生顯著的影響。因此,對於長期債券來說,面值的現值波動幅度更大。
另一件要知道的關於利率風險的事情就是,與金融和經濟領域中的許多情況類似,它是以遞減的速率增長的。換句話說,如果我們比較10年期債券和1年期債券,我們會看到10年期債券有更大的利率風險。然而,如果比較20年期債券和30年期債券,你會發現30年期債券有更大的利率風險,因為它有更長的到期期限,但是利率風險的差值很小。
較低票息的債券所包含的利率風險較高的原因也基本相同。正如我們之前所討論的,一份債券的價值依賴於其利息和麵值的現值。如果兩份債券的票面利率不同,到期期限相同,那麼較低票息的債券價值就更加依賴於在到期日時可收回的面值金額。因此,在其他條件相同的情況下,當利率變動時,其價值波動的幅度會更大。從另一個角度理解,更高票息的債券在其存續期內的早期所產生的現金流量更多,因此其價值對於貼現率的變動較不敏感。
超過30年的債券到期時間是不常見的。然而,近年來的低利率導致了一些更長期限的債券發行。在20世紀90年代,迪士尼公司發行了“睡美人”債券,到期時間為100年。類似的還有貝爾南方(BellSouth)、可口可樂以及荷蘭銀行業巨頭荷蘭銀行(ABN AMRO)都發行過到期時間為100年的債券。儘管有些罕見,但100年期債券仍在發行,最近甚至有政府在發行這類債券。例如,比利時在2015年發行了100年期債券,愛爾蘭在2016年發行了100年期債券。愛爾蘭債券最初發行時的到期收益率只有2.35%,這是我們在本章後面討論利率期限結構時需要記住的。
我們可以運用100年期的貝爾南方(AT&T)債券闡述利率風險的影響。下表中提供了這次發行的一些基本信息,以及它在1995年12月31日、2009年3月6日和2017年12月29日的價格。

本表中的一些問題浮現出來。首先,從1995年12月31日到2009年3月6日,利率明顯只有上升。(為什麼?)但那之後,利率又下降了。(為什麼?)債券的價格先是下降了19.66%然後又上升了45.14%。
7.1.4 求到期收益率:更多的試錯
通常,我們會知道一份債券的價格、票面利率和到期日,但是不會知道它的到期收益率。舉例來說,假定我們對一份6年期、票面利率為8%的債券感興趣,一名經紀人的報價為955.14美元。那麼這份債券的收益率為多少呢?
我們已經知道債券的價格可以寫作利息和麵值的現值之和。已知票面利息為每年80美元、到期期限為6年、面值為1 000美元,我們可將其價格表示為
955.14=80×[1-(1/(1+r)6)]/r+(1 000/(1+r)6)
式中,r是未知的貼現率,或者到期收益率。我們有一個等式和一個未知數,無法直接解出r。能夠找到答案的唯一方法就是試錯。
這個問題與我們在上一章試圖找出年金的未知利率非常相似。然而,還有一個1 000美元的債券面值,因此找出債券的利率(或收益率)就更為複雜。
我們可以通過所知的關於債券價格和收益率的信息,加快試錯的進程。在本例中,債券的票面利息為80美元,同時折價賣出。因此我們可以知道收益率高於8%。如果我們按照10%計算,價格為
債券價值=80×(1-(1/1.106))/0.10+(1 000/1.106)
=80×4.355 3+(1 000/1.771 6)=912.89(美元)
在10%的利率下,計算出的價值低於實際價格,因此10%過高了。真實的收益率應該處於8%~10%。在這個時候,可運用“插值法”找到正確答案。可能你接下來想嘗試9%。如果你這樣做的話,你將會發現這實際上就是該債券的到期收益率。
一份債券的到期收益率不應該與當期收益率(current yield)相混淆,債券的當期收益率就是債券的年利息與其價格的簡單相除。在剛才的例子中,債券的年利息為80美元,價格為955.14美元。給定這些數字後,我們可以計算出當期收益率等於80美元/955.14美元=8.38%,低於到期收益率9%。當期收益率過低的原因是它只考慮了收益中的利息部分,未曾考慮到從價格的折扣中所能獲得的那部分隱含利得。對於溢價發行的債券來說,反之亦然,也就是說當期收益率會較高,因為它忽略了隱含的損失。
我們關於債券估值的討論總結在表7-1中。
表7-1 債券估值概述

【例7-2】當期收益率
一份債券的標定價格為1 080.42美元。其面值為1 000美元,半年期利息為30美元,到期期限為5年。它的當期收益率是多少?到期收益率又是多少?哪個更大?為什麼?
注意到這份債券每半年支付30美元的利息,因此年支付額為60美元。當期收益率為60美元/
1 080.42美元=5.55%。為了計算出到期收益率,重新看看例7-1。在本例中,債券每6個月支付30美元利息,並有10個6個月的期間直到到期日。因此,我們需要運用下式計算出r
1 080.42=30×[1-(1/(1+r)10)]/r+(1 000/(1+r)10)
在經過一些試錯後,我們發現r等於2.1%。但是,具有一點迷惑性的是,這個2.1%是每6個月的收益率。我們要將這個數字乘以2以得到到期收益率,因此到期收益率應為4.2%,略低於當期收益率。原因在於當期收益率忽略了溢價債券在當前時點與到期日之間的隱含損失。
【例7-3】債券收益率
現有兩份除了利息和價格不同以外其他條件均相同的債券。它們的到期期限都是12年。第1份債券的票面利率為10%,售價為935.08美元。第2份債券的票面利率為12%,那麼它的售價應該是多少?
由於這兩份債券十分相似,假定它們會按照相同的收益率進行定價。我們首先需要計算票面利率為10%的債券的收益率。就像前面講到的,我們知道它的收益率高於10%,因為債券是折價發行的。該債券的到期期限較長,為12年。我們已經知道長期債券的價格對利率的變動更加敏感,所以收益率應該很接近10%。經過少數幾次試錯後,我們發現收益率實際為11%。
債券價值=100×(1-(1/1.1112))/0.11+(1 000/1.1112)
=100×6.492 4+(1 000/3.498 5)
=649.24+285.84=935.08(美元)
在11%的收益率下,第2份債券將會溢價出售,因為它的票面利息為120美元。其價值為
債券價值=120×(1-(1/1.1112))/0.11+(1 000/1.1112)
=120×6.492 4+(1 000/3.498 5)
=779.08+285.84=1 064.92(美元)
計算器使用說明 如何運用財務計算器計算債券的價格和收益率
很多財務計算器都有很好的嵌入債券價值計算程序。然而,在實際運用中,這些計算流程有很大差異,而且並不是所有財務計算器都有。因此,我們向大家展示一種在任何財務計算器上都可以解決債券問題的簡單方法。
當然首先我們要把計算器清零。接下來以例7-3為例,我們考慮兩隻債券,都是12年到期。第1只售價為935.08美元,並且有10%的年息票利率。為了計算收益率,我們可以如下操作

這裡注意到我們輸入了代表債券面值的1 000美元的終值,也輸入了代表年利息的1 000美元的10%,或每年100美元。而且,我們注意到債券價格的負號,這是我們作為債券價值輸入的。
對於第2只債券,我們知道相關收益率是11%,12年到期,12%的年息票利率。那麼它的價格是多少?為了回答這個問題,我們輸入如下值來計算債券現金流的現值

這裡出現了很重要的細節。假設我們的債券價格是902.29美元,10年到期,6%的年利率。就像我們之前提到過的一樣,大多數債券都是半年付息的。假設這隻債券就是這種情況,那麼這隻債券的收益率是多少?為了回答這個問題,我們輸入如下

注意,我們在支付那裡輸入了30美元,因為實際上我們每6個月支付了30美元。相似地,我們在N處輸入了20,因為實際是有20個6個月期間。我們計算出的收益率是3.7%。需要保持謹慎的是這是每6個月的收益率,所以我們要把這個乘以2:2×3.7=7.4%來得到正確的答案,這就是債券的報告收益率。
使用電子製表軟件 如何運用電子數據表計算債券的價值和收益率
大多數電子數據表都有完善的計算債券價值和收益率的程序。很多這些程序涉及的細節我們不做討論。然而,建立一個簡單的電子數據表來計算債券的價格和收益率是簡單容易的,就像如下展示的兩個電子數據表:
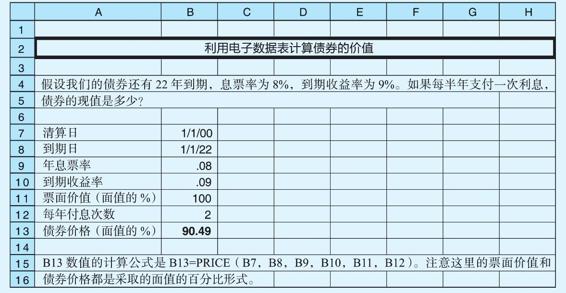
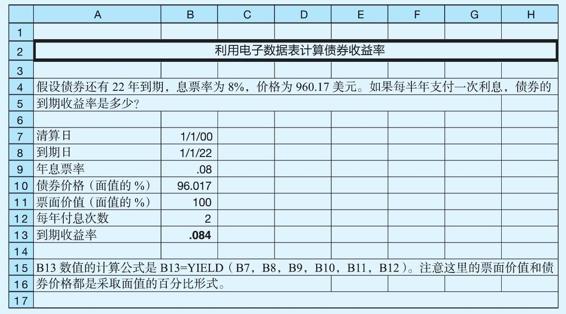
在電子數據表中,注意到我們輸入了兩個日期:清算日和到期日。清算日就是我們實際支付債券的日期,到期日就是債券實際到期的日期。在要解決的大部分問題中,我們不能明確地知道這些日期,所以要將它們補充出來。例如,因為我們債券是22年到期,我們挑選2000年1月1日作為清算日,2022年1月1日作為到期日。只要間隔22年的任何兩個日期都可以。最後,注意到我們已經輸入債券年息票率和到期收益率,接下來明確地輸入債券每年支付的利息額。
概念問題
7.1a 債券的現金流量有哪些?
7.1b 債券價值的一般表達式是什麼?
7.1c 持有債券的唯一風險是發行者不全額付款嗎?為什麼?