e1 Stephen Ross 公司理財 v12A
6.2 評估均衡現金流量:年金和永續年金
我們經常碰到涉及多期等額現金流量的問題。比如說,一種很常見的貸款償還方式是借款人在一段時間內每期償還固定的金額。幾乎所有的消費貸款(例如汽車貸款)以及住房貸款都具有固定付款額的特點,一般來說一個月支付一次。
一般來說,這種發生在每期期末的一系列等額現金流量就叫作普通年金(annuity),或者更準確地說,現金流呈普通年金形式。普通年金經常出現在財務計劃中,有一些簡便的方法可以用來確定年金價值。我們接下來會介紹這些方法。
6.2.1 年金現金流量的現值
假如我們正在對一項在未來3年中的每年年末將會支付500美元的資產進行估值。這項資產的現金流就構成了一個每年支付500美元、支付期為3年的普通年金。如果我們要求的報酬率為10%,那麼我們從這項資產中將會得到多少?
從上一節中我們可知,我們需要用10%的貼現率對每期支付的500美元進行貼現
現值=(500/1.11)+(500/1.12)+(500/1.13)
=(500/1.1)+(500/1.21)+(500/1.133 1)
=454.55+413.22+375.66=1 243.43(美元)
這種方法還不錯。不過,通常情況下,我們碰到的問題將會涉及很多期的現金流量。例如,典型的按月償還的住房貸款將會有長達30年的還款期,共360個月。如果我們想要計算這類問題的現值,使用簡單的方法將會很有幫助。
因為年金的現金流全部都相同,我們可以使用基本現值等式的一個變形。報酬率為r,投資期為t,每期支付額為C美元的年金現值為
年金現值=C×(1-現值係數)/r=C×{1-[1/(1+r)t]/r} (6-1)
大括號內的項目叫作年金現值利率係數,被簡寫為PVIFA(r,t)。
這個公式看起來有點複雜,但是使用起來很簡單。注意1/(1+r)t就是我們說的現值係數。在該例子中,t為3,利率為10%,則
現值係數=1/1.13=0.751 315
要計算年金現值係數,則需要代入這一項
年金現值係數=(1-現值係數)/r=(1-0.751 315)/0.1
=0.248 685/0.10=2.486 85
像我們之前計算的那樣,我們的500美元年金的現值為
年金現值=500×2.486 85=1 243.43(美元)
【例6-5】你可以負擔多少錢
在仔細地檢查過自己的預算後,你發現為了買一輛運動型汽車,每個月最多可以負擔632美元。在詢問了銀行後你得知,48個月的貸款利率為每月1%,你可以貸款多少?
為了得到你可以承擔的貸款數額,我們需要計算48個月,月利率為1%,每個月償付632美元的貸款現值。貸款償付呈年金形式,使用現值公式可得
年金現值係數=(1-現值係數)/r=(1-(1/1.0148))/0.01
=(1-0.620 3)/0.01=37.974 0
使用該現值係數,我們可以得到48期,每次償付632美元的貸款現值為
632×37.974 0=24 000(美元)
因此,24 000美元就是你可以承擔的貸款額。
1.年金錶
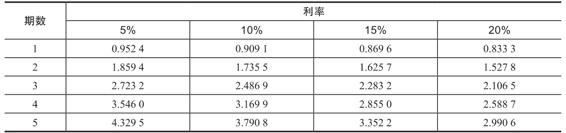
就像普通現值係數有表可查一樣,普通年金也有專門的年金現值係數表。表6-1為年金現值係數表的一小部分;附錄A中的表A-3包含了更大的部分。在計算例6-5的問題前我們可以查找該表,找到第3期對應的那一行,然後找到10%的那一列交叉對應的那個係數。你所看到的係數應為2.486 9(精確到小數點後4位),這和我們計算的一樣。試著計算一些係數,然後同表中的係數比較,以確保你知道如何計算。如果你使用財務計算器,只要輸入1美元作為付款額,然後計算現值,結果應該同年金現值係數表中的一樣。
表6-1 年金現值利率係數表
計算器使用說明 年金現值
使用財務計算器求解年金現值係數時,我們需要使用PMT鍵(你可能在想這代表著什麼)。同計算單期現值相比,計算多期現值有兩個不同。首先,使用PMT鍵輸入我們需要的年現金流量。其次,不需要輸入終值。例如,在計算3年期,每期支付500美元的例子中,如果利率為10%,我們需要做如下的事情:

同樣地,我們會得到一個為負數的現值。
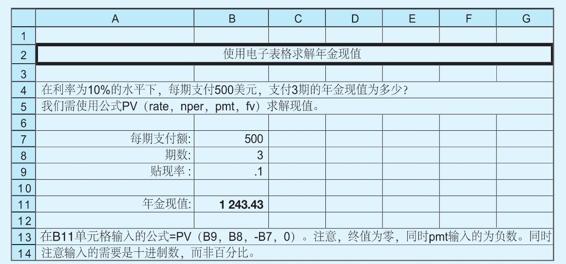
使用電子表格 年金現值
使用電子表格計算年金現值的方法如下:
2.求付款額
假設你正想創立一家新公司,主營現在流行的健康食品——凍犛牛奶。為了生產以及銷售產品,你需要借入100 000美元。因為相信這股流行凍犛牛奶的風潮不會持續太久,你計劃在5年內還清所欠的貸款。在利率為18%的情況下,每期的償還額是多少?
在這個例子中,我們知道現值是100 000美元,利率為18%,期限為5年。由於每期等額償還,因此我們必須找到相關的現值係數以求解現金流量
年金現值=100 000=C×[(1-現值係數)/r]
=C×{[1-(1/1.185)]/0.18}
=C×[(1-0.437 1)/0.18]
=C×3.127 2
C=100 000/3.127 2=31 977.78(美元)
因此,你每期大致需要償還32 000美元。
計算器使用說明 求付款額
使用財務計算器求付款額是很簡便的。在我們之前的例子中,現值是100 000美元,利率為18%,期限為5年。我們求付款額的方法如下:

在此我們得到的是一個負數,這是因為對我們而言付款是一項現金流出。
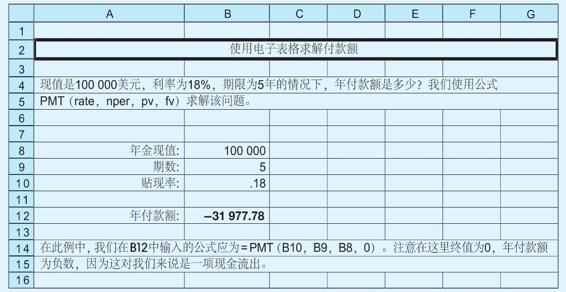
電子表格使用說明 求付款額
使用電子表格解決上面我們提到的問題的方法如下:
【例6-6】求支付期數
在春假期間你由於手頭緊張透支了1 000美元。你每月只能負擔最低的20美元還款額。信用卡的利率為每月1.5%。你需要多久才可以還清1 000美元?
在這個問題中,我們知道每月支付額為20美元,月利率為1.5%,我們需要求期數。現值是
1 000美元(你今天擁有的)。首先,我們需要做一些代數運算(或使用財務計算器)
1 000=20×[(1-現值係數)/0.015]
(1 000/20)×0.015=1-現值係數
現值係數=0.25=1/(1+r)t
1.015t=1/0.25=4
此時,問題變為在月利率為1.5%的情況下,若要讓你的錢變為現在的4倍,需要多久?根據我們之前的計算,這個答案大概是93個月
1.01593=3.99≈4
你大概需要93/12=7.75年來還清1 000美元的貸款。如果使用財務計算器來解決這個問題,需要注意有的財務計算器會自動取整。
計算器使用說明 求期數
我們需要做如下事情來解決這個問題:

注意我們需要輸入一個為負數的支付額。求出期數後,你仍需要除以12來得到我們需要的結果。同時,你需注意有些財務計算器並不會報告出分數的期數,而是會自動取整。使用電子表格解決此問題時你需要使用公式=NPER(rate,pmt,pv,fv),注意在fv處輸入0,在pmt處輸入-20。
3.求貼現率
我們需要問的最後一個問題是有關年金的利率。比如說,在你現在支付6 710美元后,保險公司承諾在之後的10年中的每個月支付你1 000美元。這個10年期年金隱含的利率是多少?
在這個問題中,我們知道現值(6 710美元)、現金流量(1 000美元)以及投資期(10年)。我們不知道的是貼現率
6 710=1 000×[(1-現值係數)/r]
6 710/1 000=6.71={1-[1/(1+r)10]}/r
因此,10年期的年金係數為6.71。我們需要求解的是這個等式裡的未知數r。不幸的是,這很難直接計算出來。求解的方法只有查表或是試錯。
如果你在本書附錄A的表A-3中沿著10期這一行查找,你會發現6.710 1對應著8%,所以我們馬上可以知道保險公司提供的利率是8%。或者我們可以通過試算不同的利率最後得到我們需要的值。使用試錯法可能比較乏味,還好機器比較擅長做這種事。[1]
我們將舉例說明如何使用試錯法。假設你的一位親戚想向你借3 000美元。她在之後的4年每年將償還1 000美元。她支付給你的利率是多少?
在這裡,現金流量以期限為4年、每年1 000美元的年金形式呈現。現值是3 000美元,我們需要求利率。我們這樣做的目的是讓你瞭解貼現率同年金價值之間的關係。
我們需要從某處開始試錯,10%的利率也許是個不錯的選擇。在10%的利率下,年金係數為
年金現值係數=[1-(1/1.104)]/0.1=3.169 9
在利率為10%的情況下,現值為
現值=1 000×3.169 9=3 169.90(美元)
你可以看到我們離結果不遠了。
10%的利率是太高還是太低了呢?回憶現值和貼現率的反向變動關係:貼現率越高現值越低,反之亦然。我們這裡求出的現值過高,因此貼現率太低了。如果我們嘗試使用12%作為貼現率,現值為
現值=1 000×[1-(1/1.124)/0.12]=3 037.35(美元)
這個貼現率還是太低了(因為現值有點高),我們嘗試一下13%的利率
現值=1 000×[1-(1/1.134)/0.13]=2 974.47(美元)
這次略低於3 000美元,所以我們知道答案在12%~13%,看起來答案似乎是12.5%。請自己多花點時間練習一下,你會發現正確答案是12.59%。
為了說明為何對未知利率的求解如此重要,讓我們看看在緬因州、佛蒙特、新罕布什爾州發行的一種彩票給予中獎人的領獎形式的選擇。在最近的一次抽獎中,中獎人可以選擇一次領取總額為250 000美元的獎金,或是在25年期間,每年等額領取總額為500 000美元的獎金。(當時總額獎金一般都是年金形式獎金的一半。)請問,哪種選擇比較好呢?
為了回答這個問題,我們需要比較現在的250 000美元和25期、每期500 000/25=20 000美元的獎金。在利率水平為多少時這兩種選擇的價值是相同的?這和我們之前的問題一樣,我們需要求的是現值為250 000美元,期數為25期,每期20 000美元的年金貼現率是多少。如果你好好算算(或通過一些計算器的幫助),會求出這個利率大致為6.24%。如果這個利率比其他投資更有吸引力的話,你應該選擇按年金方式領獎。注意,我們在這個例子中忽略了稅的問題,然而稅會對我們的結果造成很大的影響。如果你中了彩票,請諮詢你的稅務顧問。
在另一個例子中,2014年年初,沃倫·巴菲特和Quicken Loans的創始人丹·吉爾伯特聯手,為猜對2014年美國男子大學生籃球聯賽(NCAA)全部比賽結果的人提供10億美元獎金。獲勝的概率為9.2萬億分之一!當然,即使你都猜對了,也不會在今天得到10億美元,而是40年內每年2 500萬美元,或者一次性得到5億美元。看看你是否同意這種安排的收益率是3.93%。
計算器使用說明 求貼現率
你可以選擇使用財務計算器來求解貼現率。
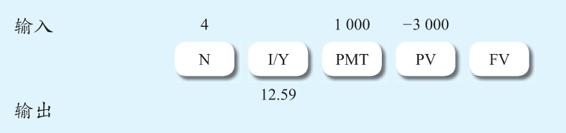
注意我們輸入的現值是一個負數(這是為什麼?)。使用電子表格求解貼現率時,我們使用的公式是=RATE(nper,pmt,pv,fv)。注意在這個例子中,fv為0,pv為-3 000。
6.2.2 年金現金流量的終值
有些時候,求年金的簡便方法會很實用。如你猜想的一樣,有年金現值係數就有年金終值係數。年金終值係數的一般形式如下
年金終值係數=(終值係數-1)/r=[(1+r)t-1]/r (6-2)
為了說明如何使用年金終值係數,假設你每年向退休賬戶存入2 000美元,年利率為8%。你將會在30年之後退休,退休時你將會有多少錢?
時間t在這裡等於30,利率r等於8%;因此年金終值係數等於
年金終值係數=(終值係數-1)/r=(1.0830-1)/0.08
=(10.062 7-1)/0.08=113.283 2
這筆期限為30年,每年支付2 000美元的年金終值為
年金終值=2 000×113.28=226 566.42(美元)
計算器使用說明 求年金終值
同樣地,你也可以使用財務計算器解決該問題:

注意我們輸入的現值是一個負數(這是為什麼?)。使用電子表格求解貼現率時,我們使用的公式是=FV(rate,nper,pmt,pv)。注意在這個例子中,PV為0,PMT為-2 000。
有時候,我們需要由年金終值求解未知利率r。例如,如果你在1978年12月之前的25年間,每年投資股票100美元,你的投資最終將會變為76 374美元。然而這卻是1925~2016年之間所有25年期投資的報酬最差的一期,差到什麼程度呢?
在這裡我們知道每期現金流量為100美元,終值為76 374美元,期限為25年(或者300個月),我們需要求隱含利率r
76 374=100×[(終值係數-1)/r]
763.74=[(1+r)300-1]/r
由於這期間的投資回報率最差,我們從1%開始試算
年金終值係數=(1.01300-1)/0.01=1 878.85(美元)
我們發現1%過高,經過試算r大約為每月0.55%。同時你在本章的後面會知道,這相當於每年6.8%。
6.2.3 關於預付年金的說明
到目前為止我們只討論了普通年金。普通年金很重要,但是還有一種年金的變形很常見。請記住在普通年金中,每期的現金流發生在期末。當你以每月償還的方式取得一筆貸款時,第1筆還款通常發生在你取得貸款後的那一期的期末。然而,當你租一間公寓時,第1筆租金通常需要馬上支付。第2種年金的還款發生在每期的期初。租賃是預付年金(annuity due)的一個例子。預付年金的支付發生在每期的期初。幾乎所有的每期償還等額款項的安排都是預付年金。
計算預付年金的方法有許多種。使用財務計算器進行計算時,你只需要將模式調到“預付”或是“期初”就可以了。記得在你計算之後再將狀態調回來!另一種計算預付年金的方法是使用時間軸。假設一個預付年金每期支付400美元,支付期為5年,貼現率是10%。時間軸如下

注意除了在0時點有一個額外的400美元現金流之外,這裡的現金流和一個4年期的普通年金一樣。我們求出4年期普通年金的現值為1 267.95美元。如果加上額外的400美元,我們得到1 667.95美元,這就是預付年金的現值。
還有一種更為簡單的求解預付年金的方法。如果我們假定現金流發生在每期期末,但實際上現金流發生在每期期初,我們需要將現金流向前貼現一期。我們只需將答案乘以(1+r),其中r是貼現率。實際上,普通年金現值和預付年金現值的關係如下
預付年金現值=普通年金現值×(1+r) (6-3)
這個式子對於現值和終值都成立。因此計算預付年金共需要2步:第1步,計算出普通年金的現值或終值;第2步,將你的答案乘以(1+r)。
6.2.4 永續年金
我們已經知道,一系列等額的現金流可以被視為年金。一種特殊情況是現金流的期限會無限持續下去,這種年金叫作永續年金(perpetuity)。永續年金有時被稱為統一公債(consol),特別是在加拿大和英國。例6-7就是關於永續年金的一個重要例子。
由於永續年金擁有無限期的現金流,我們無法通過將每期現金流貼現來求其現值。幸運的是,永續年金的估價是所有情況中最簡單的一種。永續年金現值就是
永續年金現值=C/r (6-4)
比如說,一項投資每年可提供500美元的永續年金。你的投資回報率是8%,這項投資的價值是多少?投資價值為
永續年金現值=C/r=500/0.08=6 250(美元)
表6-2總結了上述年金以及永續年金的計算過程。至此,你可能認為你將會採用在線計算器解決年金的問題。
表6-2 年金及永續年金計算總結

【例6-7】優先股
優先股是永續年金的一個重要的例子。當一個公司發售優先股時,承諾向購買者每期(通常是每季度)支付固定、無限期的股利。這種股利先於普通股股利支付,這就是優先權的含義。
假如Fellini公司計劃以每股100美元的價格發售優先股。已經在外流通的類似優先股的每股價格是40美元,每季度支付1美元的股利。對於這種新發售的優先股,Fellini每季度應支付多少股利?
已發售的優先股的現值為40美元,每季度提供1美元的永續現金流。由於這是永續年金,因此
現值=40=1×(1/r)
r=2.5%
為了提高競爭力,Fellini公司的新股也應該在每季度支付2.5%的股利;如果新股現值為100美元,股利應該為
現值=100=C/(1/0.025)
C=2.5(美元)(每季度)
6.2.5 增長年金與增長型永續年金
通常來說,年金支付金額會隨著時間的增長而增長。比如說,假設我們要分析一項支付期為20年的彩票中獎金額情況。200 000美元的首筆支付將會發生在1年之後。之後的每一年,支付額將會增加5%,因此第2年的支付額為200 000美元×1.05=210 000美元。第3年的支付額是210 000美元×1.05=220 500美元,依此類推。在貼現率為11%的情況下,彩票中獎金額的現值是多少?
如果使用符號g代表增長率,我們將會使用普通年金公式的修正形式求解現值
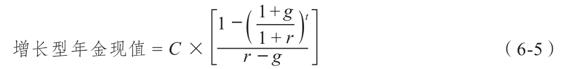
將我們的彩票例子中的數據代入該公式後(並且令g=0.05),我們得到
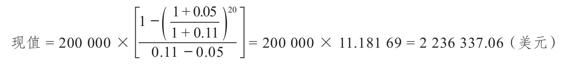
這裡也有計算增長型永續年金現值的公式
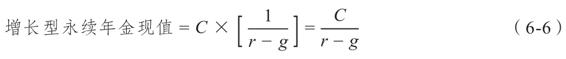
在我們的例子中,現在我們假定支付是無限期的。在這種情況下,現值為
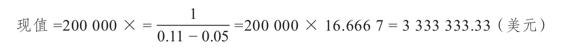
因為每期的支付額都在增長,所以增長型永續年金這一概念顯得有些奇怪;但是在我們之後的章節中你會發現,增長型永續年金在有關股票價格的分析中扮演著很重要的角色。
在我們繼續學習之前,請特別注意,關於這裡給出的增長年金以及增長型永續年金的計算公式,有一點很重要。在這兩個公式中,現金流C都是從現在算起恰好在一期之後將會發生的現金流。
概念問題
6.2a 總的來說,在利率為r的情況下,每期支付額為C的年金現值是多少?終值是多少?
6.2b 總的來說,永續年金的現值是多少?
[1] 財務計算器使用試錯法求解該問題。這就是為什麼有時候答案出來前屏幕顯示的是“計算中”。事實上,如果期數少於5期,通過直接計算也能求出r,但是通常不值得這麼麻煩。