e1 Stephen Ross 公司理財 v12A
6.1 多期現金流量的現值和終值
到目前為止,我們僅將注意力侷限在一個當前總額的終值,或是某種未來單個現金流量的現值。在本章我們將會開始對多期現金流進行估值。我們從終值開始介紹。
6.1.1 多期現金流量的終值
假如你今天在一個利率為8%的賬戶中存入了100美元。1年後,你將會再存入100美元。2年後你將有多少錢?這個問題相對來說很簡單。在第1年年末,你將得到108美元,再加上你存入的第2個100美元,一共208美元。你將這208美元在利率為8%的水平下再存1年,在第2年的期末你將會得到
208×1.08=224.64(美元)
圖6-1是一條時間軸,它說明了這兩個100美元的計算過程。解決此類複雜問題的時候,這類圖是很有用的。當你遇到計算終值或是現值問題的困難時,畫一條時間軸可以幫你看清問題發生的情形。
在圖6-1的第一部分,在時間軸上展示了現金流量。最重要的是,我們把它們標註在實際發生的時間點上。在此,第1筆現金流發生在今天,標記為時間點0。因此我們將100美元標記在時間點0的位置上。第2個100美元發生在1年之後,我們將它標註在時間點1的位置上。在圖6-1的第二部分,以一次計算一期終值的方式,我們得到終值為224.64美元。

圖6-1 畫出並使用時間軸
【例6-1】重談儲蓄
你認為你有能力在接下來的3年中每年存4 000美元於一個利率為8%的銀行賬戶內。你目前在這個賬戶裡有7 000美元。3年之後你會有多少錢?4年之後呢?
第1年年末你將會有
7 000×1.08+4 000=11 560(美元)
第2年年末你將會有
11 560×1.08+4 000=16 484.80(美元)
第3年年末你將會有
16 484.80×1.08+4 000=21 803.58(美元)
因此,3年後你將會有21 803.58美元。如果你再存1年(不再向該賬戶增加投入),第4年年末你將會有
21 803.58×1.08=23 547.87(美元)
當我們計算兩個100美元終值時,只需計算每年年初餘額,再將其向前滾動一年。還有一個更快捷的方法,第1個100美元可以看作在8%的利率下存了2年,因此其終值為
100×1.082=100×1.166 4=116.64(美元)
第2個100美元可以看作在8%的利率下存了1年,因此其終值為
100×1.08=108(美元)
總值等於這兩個終值的和
116.64+108=224.64(美元)
根據這個例子,我們有兩種方法計算多期現金流終值:①將累計餘額每次向前複利一年;②分別計算現金流量終值,再彙總。兩種方法得出的結果是一樣的,你可以任意選擇其中一種。
為了說明這兩種不同的現金流量計算方法,我們來考慮接下來的5年中每年年末投資2 000美元的終值。目前餘額為0,利率為10%。我們首先畫出一條時間軸,如圖6-2所示。
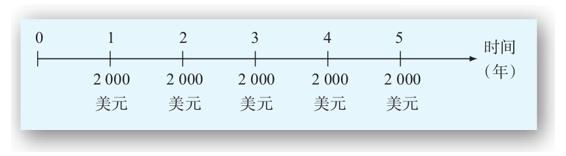
圖6-2 5年期,每年2 000美元的時間軸
注意在該時間軸上,直到第1年的年末才有第1筆2 000美元的投資。第1筆2 000美元投資將會賺取之後4年(不是5年)的利息。同時需要注意的是,最後一筆投資在第5年年末投入,因而它沒有賺取任何利息。
圖6-3說明了將資金金額一次複利一期的計算方法,終值為12 120.20美元。

圖6-3 以每次向前複利一期的方式計算終值
圖6-4採用了第2種計算方法,結果相同。
【例6-2】再談儲蓄
如果第1年存了100美元,第2年存了200美元,第3年存了300美元,3年後你將會有多少錢?其中多少是利息?假設你不再多存入資金,第5年你將會有多少錢?假設利率為7%。

圖6-4 以分別複利每一筆現金流量的方式計算現值
我們將要計算每筆金額在3年後的價值。注意,有100美元賺取了2年的利息,200美元賺取了1年的利息。最後的300美元沒有賺取利息,終值為

因此,終值總額為628.49美元。利息總額為
628.49-(100+200+300)=28.49(美元)
5年後你將會有多少錢?我們知道3年後你將會有628.49美元,如果你將它再存2年,它將會變為
628.49×1.072=628.49×1.144 9=719.56(美元)
注意,我們可以分別計算每筆金額的終值。同樣地,仍需注意存入時間的長度。如我們之前算的一樣,第1筆100美元只賺取了4期的利息,第2筆存款賺取了3期的利率,最後一筆存款賺取了2期的利息

6.1.2 多期現金流量的現值
我們經常需要計算一系列未來現金流的現值。如計算終值一樣,有兩種方法可以計算現值:可以每次貼現一期,或者將每筆現金流單獨貼現並且最後彙總。
假如1年後你需要1 000美元,2年後你需要2 000美元。投資回報率為9%,你今天需要投資多少以滿足你未來的需求?換句話說,這2期現金流的現值是多少?
2年後的2 000美元,在利率為9%的水平下的現值為
2 000/1.092=1 683.36(美元)
1年後的1 000美元,在利率為9%的水平下的現值為
1 000/1.09=917.43(美元)
因此,總現值為
1 683.36+917.43=2 600.79(美元)
要知道為什麼2 600.79美元為正確答案,我們可以看看2年後,當我們付出2 000美元后是不是沒有錢剩下。如果我們將2 600.79美元投資於1年期利率為9%的項目,我們將會有
2 600.79×1.09=2 834.86(美元)
我們取出1 000美元,留下1 834.86美元,在9%的利率下再投資1年,我們將會有
1 834.86×1.09=2 000(美元)
這和我們計劃的一樣。這個例子告訴我們,一系列未來現金流量的現值,就是在利率給定的情況下,為了完全複製未來的現金流,你在今天所需要的金額。
另一種計算未來現金流現值的方法是每次貼現一期。舉例來講,假設我們投資於一個在未來5年中每年期末都支付1 000美元的項目。為了得到現值,我們將每個1 000美元分別貼現,最後彙總。圖6-5展示了這種方法;如圖6-5所示,在貼現率為6%的情況下,答案是4 212.37美元(忽略微小差異)。

圖6-5 以分別貼現每筆現金流量的方式計算現值
此外,我們還可以將最後一筆現金流貼現到前一期,然後將其加到倒數第2期
(1 000/1.06)+1 000=943.40+1 000=1 943.40(美元)
我們再將該金額向前貼現一期,並將其加到第3期
(1 943.40/1.06)+1 000=1 833.40+1 000=2 833.40(美元)
這個過程可以根據需要而重複。圖6-6展示了該計算過程。

圖6-6 以每次向前貼現1期的方式計算現值
【例6-3】它值多少錢
你有一項投資,預期第1年會回報你200美元,第2年回報你400美元,第3年600美元,第4年800美元。你對投資要求的報酬率為12%。那麼為了該筆投資你最多可以支付多少錢呢?
我們需要計算在12%的報酬率下,這些現金流量的現值。將每筆現金流分別貼現,得到

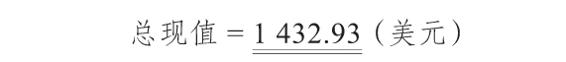
若你的投資回報率為12%,你可以投資1 432.93美元於這個項目,這是你願意支付的最大金額。
【例6-4】它值多少錢(第二部分)
某項投資提供給你3次每次5 000美元的付款,第1次付款在4年後,第2次在5年後,第3次在6年後。你可以得到11%的報酬,那麼該投資在今天的現值是多少?這些現金流的終值是多少?
我們將首先回答第2個問題來進行說明。這些現金流6年後的終值為
5 000×1.112+5 000×1.11+5 000=6 160.50+5 550+5 000=16 710.50(美元)
現值為
16 710.50/1.116=8 934.12(美元)
我們檢驗一下。每次考慮一筆現金流,那麼這些現金流的PV為

答案完全相同。需要說明的是,計算終值和現值的先後次序並不重要,我們可以選擇最簡便的方法。只要貼現率和期數不搞錯,答案一定是一樣的。
計算器使用說明 怎樣使用財務計算器計算多期現金流量現值
這並不是一個新的問題。使用財務計算器計算多期現金流量現值和我們之前介紹的方法一樣。不過,在此,我們將會教你一個簡單的方法,以例6-3的數據為例。
我們首先清空財務計算器。在例6-3中,第1個現金流量為200美元,貼現率為12%,因此我們輸入:

現在可以記下得出的數字,但這樣做效率不高。實際上,財務計算器可以存儲數據。為什麼不這樣做呢?使用財務計算器的存儲功能將會使得計算更為快捷。
接下來我們計算第2筆現金流。輸入N等於2,FV等於400。我們不需要改其他數據。

將這個數字與上一步計算中你保存的數字進行相加,以保存這個數字,之後的兩個數字也這樣處理。
我們之後的章節將會教你如何將所有的現金流量一次性輸入。
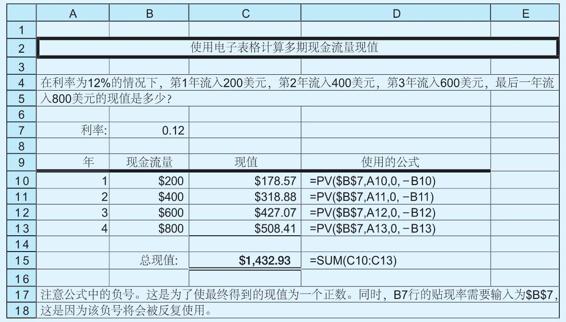
使用電子製表軟件 怎樣使用電子製表軟件求解多期現金流量現值
和之前章節所做的一樣,我們需要創建一個基本電子表格來計算每一期現金流量的現值,注意我們只是簡單地將每一期現金流量貼現後加總。
6.1.3 關於現金流量時點的說明
在解決有關現值或是終值的問題時,現金流的時點非常重要。在幾乎所有的計算中,我們都假設現金流在每期期末發生。事實上,我們討論過的所有模型、現值表和終值表,以及所有財務計算器的預設都假設現金流在每期期末發生。除非另有說明,否則應該假設它包含這個意思。
舉例說明這一點,假設你知道有一個3年期的投資,它第1年的現金流量為100美元,第2年的現金流量為200美元,第3年的現金流量為300美元,你需要畫出時間軸。在沒有其他信息的情況下,你將假設時間軸總會是這樣的形式

在我們的時間軸上,注意第1筆現金流發生在第1期的期末,第2筆現金流發生在第2期的期末,第3筆現金流發生在第3期的期末。
在本節的最後,我們將會解答在本章開頭所講的有關安德魯·拉克的合約的問題。回憶一下,該筆合同規定了640萬美元的簽約獎勵,以及將在2016年支付的1 200萬美元。餘下的1.207 25億美元包括將在2017年支付的1 940萬美元,2018年支付的2 440萬美元,2019年支付的2 752.5萬美元,2020年支付的2 840萬美元,2021年支付的2 100萬美元。如果合適的貼現率為12%,那麼小馬隊真正支付的是多少錢呢?
為了回答這個問題,我們將每年的支付額貼現到當期(注意我們假定每期的支付都在期末):
第0年(2016年)18 400 000=18 400 000(美元)
第1年(2017年)19 400 000×1/1.121=17 321 428.57(美元)
第2年(2018年)24 400 000×1/1.122=19 451 530.61(美元)
…
第5年(2021年)21 000 000×1/1.125=11 915 963.97(美元)
如果你逐年算出答案並加總(做一下試試),你將會發現安德魯的合同的現值為1.047億美元,是合同標明價值1.391 25億美元的75%。
概念問題
6.1a 說明怎樣計算一系列現金流量的終值。
6.1b 說明怎樣計算一系列現金流量的現值。
6.3c 除非另有說明,否則我們對終值和現值的時點的假設是什麼?