e1 Stephen Ross 公司理財 v12A
5.3 終值和現值的進一步講解
回顧一下終值和現值的表達式,你會發現它們之間有一種簡單的關係。本節將會探討這種關係,以及和這種關係有關的問題。
5.3.1 終值和現值
我們所說的現值係數其實就是終值係數的倒數(即1除以)
終值係數=(1+r)t
現值係數=1/(1+r)t
事實上,很多財務計算器計算現值係數的方法都是先計算終值係數,之後再按“1/x”鍵,反過來求現值係數。
如果我們令FVt代表t期後的終值,則終值和現值的關係可以簡單寫為
PV×(1+r)t=FVt (5-3)
PV=FVt/(1+r)t=FVt×[1/(1+r)t]
這個最終的結果叫作基本現值等式。我們將會在這本書中反覆用到它。與這個等式相關的變化形式有很多,但是這個簡單的等式說明了公司理財中許多重要概念的原理。
【例5-8】投資估值
我們將會通過下面有關投資的簡單例子說明怎樣使用終值和現值。你的公司將要購買一項價值335美元的資產,這項投資是安全的,3年後你將以400美元的價格出售該項資產。你知道可以將335美元投資於利率為10%且風險水平很低的其他項目。你認為這項購買資產的投資怎麼樣?
這不是一個好的投資。為什麼?因為你可以將335美元投資於報酬率為10%的其他項目。這樣的話,3年後你將會獲得
335×(1+r)t=335×1.13=335×1.331=445.89(美元)
由於這項購買資產的投資最終只會使你得到400美元,因此這並不如其他的備選項目。另一種判斷投資好壞的方法是計算3年後收到的400美元在利率為10%的情況下的現值
400×[1/(1+r)t]=400/1.13=400/1.331=300.53(美元)
這個結果告訴我們,我們只需要投資300美元左右,3年後就可以得到400美元,而不需要花335美元。稍後我們還會進行類似的討論。
5.3.2 確定貼現率
我們經常需要計算一項投資隱含的貼現率。我們可以通過基本現值等式解決這個問題
PV=FVt/(1+r)t
這個等式中只包含四個部分:現值(PV)、終值(FV)、貼現率(r)、投資期(t)。給出任何3個變量,我們都可以求出第4個。
【例5-9】求單期投資的貼現率r
你在考慮一個單期投資。如果投入1 250美元,1期後將會得到1 350美元。這項投資的報酬率是多少?
首先,在這項單期投資中,答案是顯而易見的。基於1 250美元的投資,你得到了100美元的回報。隱含的投資回報率為100/1 250=8%。
從基本現值等式來看,我們知道現值為1 250美元(你今天投入的錢)。終值(現值增長到的金額)為1 350美元,投資期為1期,因此
1 250=1 350/(1+r)1
1+r=1 350/1 250=1.08
r=8%
當然,在這種簡單的例子中我們沒必要一步一步計算。但是我們之後討論期數大於1的問題時,計算就會比較困難了。
為了說明多期的情況,假設我們將會投資於一項現值為100美元,且8年後將會使我們資金翻倍的項目。為了將這個項目同其他項目進行比較,我們需要知道隱含的貼現率是多少。這裡,貼現率也叫投資回報率。在這個例子中,現值為100美元,終值為200美元,期限為8年。為了計算回報率,我們需要通過基本現值等式
PV=FVt/(1+r)t
100=200/(1+r)8
也可以表述為
(1+r)8=200/100=2
我們現在需要求r,有3種方法可以選擇。
(1)使用財務計算器。
(2)等式兩邊各開8次方根。由於開8次方根相當於1/8次方,即0.125。因此我們可以利用計算器上的“yx”鍵得到。只需輸入2,然後按“yx”鍵,再鍵入0.125,最後按“=”鍵。八次方根應該為1.09,這意味著r等於9%。
(3)使用終值表。8年後的終值係數為2,如果在本書附錄A中的表A-1中,沿著8期這一行向右找,你將會發現終值係數2對應著9%這一列。因此隱含報酬率為9%。
實際上,在這個例子中有一個粗略但有用的方法可以求r,即72法則。在合理的報酬率下,使投資額翻倍的時間大致為72/r。在我們的例子中,這意味著72/r=8,r等於9。在貼現率介於5%~20%時這個方法相當準確。
【例5-10】運動鞋收藏投資
2016年12月,史蒂芬·庫裡用塗鴉風格寫著“奧克蘭堅強”(Oakland Strong)的球鞋被拍賣,錢款捐給奧克蘭消防基金,那雙鞋最終以30 101美元成交。一個現役的NBA球員穿籃球鞋的記錄是2008年奧運會上科比·布萊恩特穿過的一雙球鞋,售價為37 740美元。有“專家”認為,這類收藏品的價值將在10年內翻一番。
那麼投資這個合算嗎?根據72法則,既然那些“專家”預測球鞋的價格將會翻倍,他預測的報酬率也不過就是72/10=7.2,即每年7.2%而已。
至少在某一段時間裡,藝術品收藏圈子中的經驗法則是“你的錢5年將會回本,10年將會翻倍”。假定它成立,讓我們看一下一項投資看起來怎麼樣。2013年,畢加索的畫作《夢》(Le Rêve)以1.55億美元售出。這幅畫其實已不全是原作,因為它的所有者、賭場大亨史蒂夫·韋恩不小心用胳膊肘在畫上戳出了一個大洞(之後他花重金請來高手對畫面進行了修復)。韋恩在12年前的2001年以6 000萬美元的價格買下了這幅畫。那麼韋恩在這場賭博中是贏家嗎?
經驗法則告訴我們,我們的錢會在10年後翻倍,所以根據72法則,我們的投資回報率為7.2%。這幅畫幾乎剛好在12年後出售,現值為6 000萬美元,終值為1.55億美元,我們需要求解利率r
60 000 000=155 000 000/(1+r)12
(1+r)12=2.583 3
求解r,我們發現出售者的投資回報率大致為8.23%,大於根據經驗法則得來的7.2%。
那麼其他的收藏品怎麼樣呢?對於一個集郵家(像你我這樣的)而言,最值得驕傲的就是1918年24美分面值的反版Jenny C3a。這版郵票值得收藏是因為它有一幅顛倒了的雙翼飛機圖案。在2016年,一枚這樣的郵票在拍賣會上賣出了1 175 000美元。它的價值增長比率是多少?你可以驗算一下,假設期限為98年,這個問題的答案是17.02%。
可收集的汽車也可以有很好的回報。例如,據報道,1939年一輛嶄新的阿爾法羅密歐8C 2900B Lungo蜘蛛售價1 150英鎊。當它在2016年被拍賣,以1 980萬英鎊的售價成為迄今為止最昂貴的戰前汽車。假設77年過去了,看看你是否同意汽車價值每年增長13.50%。
並不是所有藏品的表現都這麼好。同樣是在2016年,一枚1792年制的銀幣拍賣得了352 500美元。這枚銀幣被認為是美國造幣廠以外的第一枚銀幣。也許對於圈外人來講這是一筆很大的回報,但經過計算得知,這枚金幣在224年中的年報酬率僅為8.07%。
最稀有的硬幣之一是舊金山造幣廠鑄造的1894年的一角硬幣。只製造了24枚,其中9枚據信仍存於世。2016年,其中一枚一角硬幣以200萬美元的價格拍賣。你可以算一下看看這枚硬幣的年投資回報率是不是14.77%。
另一個更為極端的例子是關於1790年4月17日去世的本傑明·富蘭克林遺贈的錢。在他的遺囑中,他贈給馬薩諸塞州和波士頓市1 000磅銀幣;同時,也贈給賓夕法尼亞州和費城差不多的錢。這些錢來自他從政期間的報酬,但是富蘭克林認為政治家不應該收取報酬(這個觀點沒有被現代社會的政治家廣泛認同)。
富蘭克林本來規定這筆錢要在他死後100年再拿出來,並主要用於對年輕人的培訓。然而經過一番法律上的角逐後,最終協定於1990年,也就是富蘭克林去世200年後將這筆錢拿出來。當時,賓夕法尼亞州獲得的贈金已經達到了200萬美元。馬薩諸塞州的贈金達到了450萬美元。這些錢用於幫助波士頓和費城的富蘭克林機構設立基金。假設1 000磅銀幣價值1 000美元,這兩個州的報酬率是多少?(1792年美元才成為美國的官方貨幣。)
對於賓夕法尼亞州而言,終值為200萬美元,現值為1 000美元。期間為200年,因此我們需要在下式中求出r
1 000=2 000 000/(1+r)200
(1+r)200=2 000
求解r我們得到,賓夕法尼亞州的錢以每年3.87%的速度增長。馬薩諸塞州的錢表現會更好一些,驗算一下報酬率為4.3%。微小的報酬率差異累積起來居然有這麼大!
計算器使用說明
我們將會舉例說明如何使用財務計算器計算利率r。計算賓夕法尼亞州的回報率,你需要做:

同我們之前介紹過的一樣,計算的時候注意現值的符號。計算馬薩諸塞州的回報率時,你需要做什麼改變?
【例5-11】攢錢上大學
假設8年後你需要大概80 000美元用來送孩子上大學,你現在有35 000美元,投資回報率為20%,你可以攢夠錢嗎?投資回報率為多少時你可以攢夠錢?
如果你的投資回報率為20%,期限為8年,現值為35 000美元,終值為
FV=35 000×1.208=35 000×4.299 8=150 493.59(美元)
因此你可以很輕鬆地攢夠錢。最低報酬率即下式中未知的r,其計算如下
FV=35 000×(1+r)8=80 000(美元)
(1+r)8=80 000/35 000=2.285 7
因此,終值係數為2.285 7。查附錄A,表A-1中,8期所對應的那一行,我們的終值係數大致介於10%(2.143 6)和12%(2.476 0)之間。因此你的最低投資回報率大致為11%。我們也可以使用財務計算器計算回報率r
(1+r)8=80 000/35 000=2.285 7
1+r=2.285 7(1/8)=2.285 70.125=1.108 9
r=10.89%
【例5-12】離退休只有18 262.5天了
50年後你希望將以百萬富翁的身份退休。如果你今天有10 000美元,為了達到你的目標,報酬率需要為多少?
終值為1 000 000美元,現值為10 000美元,期限為50年。我們需計算未知的貼現率
10 000=1 000 000/(1+r)50
(1+r)50=100
終值係數為100。你可以驗算得出隱含報酬率大約為9.65%。
注意在現實世界中,計算增長率或者報酬率時不考慮貨幣時間價值的話往往會產生誤導性數據。例如,最受喜愛(或是憎恨)的棒球隊,紐約揚基隊1988年賽季的薪水最高,大約為1 900萬美元。2016年,洛杉磯道奇隊是薪水最高的球隊,薪水是令人難以置信的2.23億美元:增長了1 074%!如果歷史能夠作為未來的指示,我們可以大致算出棒球隊未來薪水的增長。你可以驗算一下,棒球隊薪水的年度可持續增長率為9.19%,遠遠小於剛剛計算得出的1 074%。
那麼對於古代的地圖呢?幾年前,1507年在羅馬印製的第一幅美國地圖賣出了135 000美元,價格比10年前的80 000美元增長了69%。如果你是這個地圖的所有者,那麼你10年間的投資回報率是多少?計算得知,你的年報酬率為5.4%,遠小於所報道的69%的價格增長率。
無論是針對棒球隊的薪水,或是地圖,所談的報酬都沒有考慮貨幣的時間價值,這很容易產生誤導。但並不是僅僅只有對此沒有研究的人會犯此類錯誤。一份著名的商業雜誌最近一篇文章的標題就是道瓊斯工業指數在5年內將會飆升70%,這是否意味著你的年投資回報率就是70%呢?好好想想吧。
5.3.3 求解期數
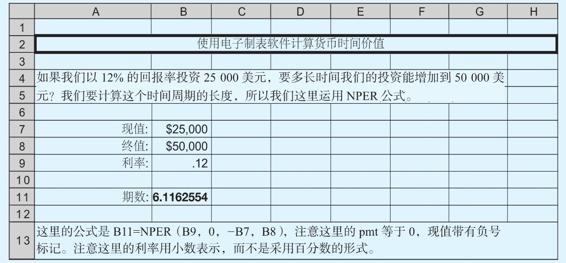
假如我們將要購買一項價值50 000美元的資產,現在有25 000美元。如果投資回報率為12%,我們需要多久可以得到50 000美元?答案是需要求出基本現值等式的最後一個變量:期數。你已經知道如何得到這個特定問題的大概答案了。注意你需要使你的錢翻倍。由72法則可知,在利率為12%的情況下,這將需要72/12=6年。
為求出精確的答案,我們可以再次採用基本現值等式。現值為25 000美元,終值為
50 000美元。在貼現率為12%時,基本等式為
25 000=50 000/1.12t
50 000/25 000=1.12t=2
我們的終值係數為2,我們現在需要求解期數t。如果你查看錶A-1中12%的那一列,你將會看到終值係數1.973 8對應著6期,因此這將需要6年達成目標。為了得到準確的答案,我們需要求t(或者使用財務計算器)。如果你這樣做,將會看到答案為6.116 3年,和我們的近似答案非常接近。
計算器使用說明
如果使用計算器,以下是你需要使用的相關變量:

【例5-13】等待收購Godot
你正存錢準備收購Godot公司。這大概需要1 000萬美元。你現在有230萬美元。如果投資回報率為5%,你需要等待多久?如果投資回報率為16%呢?
在投資回報率為5%的情況下,需要等待很長時間。從基本現值等式中我們可以看到
2 300 000=10 000 000/1.05t
1.05t=4.35
t=30(年)
在投資回報率為16%的情況下,情況好一些,你大概需要等待10年。
回到我們開篇討論的美國的EE儲蓄債券。你可以以其面值50美元的一半來購買。換句話說,今天你只需要付出25美元就可以在未來的某個時點,在債券到期的時候得到50美元。債券到期之前你不會收到任何利息,且債券的利率每6個月就會調整一次。因此,你的25美元增長到50美元所需時間的長短取決於未來的利率。但是,即使是在最壞的情況下,也能保證第20年年末可以得到50美元,這就是你需要等待的最長年限。如果你需要等待整整20年,你的投資回報率是多少?
由於這項投資會使你的錢在20年內翻倍,72法則告訴我們投資回報率為72/20=3.6%。記住,這是保證的最低報酬率,你的實際報酬可能高於這個數值。這個例子結束了我們對於基本時間價值概念的介紹。表5-4總結了現值和終值的計算,以備未來參考。
概念問題
5.3a 什麼是基本現值等式?
5.3b 什麼是72法則?
表5-4 時間價值計算總結


使用電子製表軟件 使用電子製表軟件計算貨幣時間價值
越來越多不同領域的商務人士(不單單是財務與金融領域)開始依靠電子製表軟件解決遇到的計算問題。因此,在這一節我們將會介紹如何使用財務報表解決我們之前談到的有關貨幣時間價值的問題。
我們將會介紹使用Microsoft Excel的方法,這種操作方法在你使用其他類型的軟件時可以通用。我們假設你已經熟悉了基本的軟件操作流程。
像我們知道的那樣,終值、現值、貼現率、期限這4個變量給出任意3個,可以求解出第4個。在使用電子製表軟件時,求解每一個變量都有一個單獨的公式。在Excel中所需的公式見下表:

在這些公式中,PV和FV分別代表現值和終值,NPER代表期數,RATE代表貼現率(或者利率)。
這裡我們將給出兩個小提示。首先,和財務計算器不同,輸入電子製表軟件的利率需要是十進制的。其次,就像使用財務計算器那樣,在求解利率或是期數的時候需要給輸入的現值或是終值加一個負號。
我們現在將回顧這章中的一個例子來說明怎樣使用這些公式。假如你將投資25 000美元於一個投資回報率為12%的項目,你的錢多久可以變為50 000美元?你需要創建一個如下圖所示的電子表格: