e1 John Hull 風險管理與金融機構 v5
附錄H
特徵向量和特徵值
考慮一個n×n矩陣A,假定x為一個n×1的向量,考慮方程
Ax=λx
(H-1)
以上方程可以寫為
(A-λI)x=0
其中I為n×n單位矩陣(在該n×n矩陣中,對角元素為1,非對角元素均為0)。顯然x=0是式(H-1)的解,但在什麼條件下,以上方程具有非零解呢?線性代數的一個定理保證,如果A-λI的行列式為零,那麼式(H-1)有非零解。滿足以上方程的λ就是滿足令A-λI的行列式為零的一個n次多項式的解,一般來講,這個n次多項式有n個解,這些解被稱為是矩陣A的特徵值,對應於某個特徵值,滿足式(H-1)的向量x為特徵向量。一般來講矩陣A有n個特徵向量,即每一個特徵值會對應一個特徵向量。
作為一個簡單例子,假定
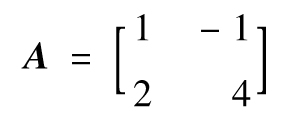
這時

以上矩陣的行列式等於
(1-λ)(4-λ)-(-1)×2=λ2-5λ+6
以上的解為λ=3及λ=2,這兩個值即為矩陣的特徵值。
為了確定對應於λ=3的特徵向量,我們對式(H-1)求解,即
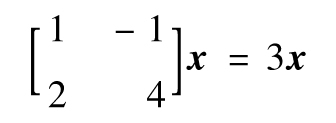
令
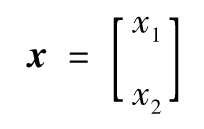
以上方程等價於
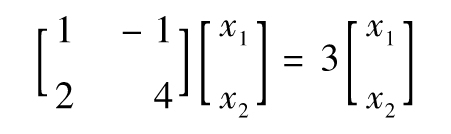
與此相對應的聯立方程為
x1-x2=3x1
及
2x1+4x2=3x2
以上兩個方程均等價於
x2+2x1=0
以上方程說明當λ=3時滿足x2=-2x1的任意x1和x2均滿足以上方程。一種約定是選取x1和x2保證向量x的長度為1,這意味著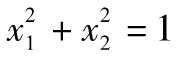 ,這時滿足x的長度為1的解為
,這時滿足x的長度為1的解為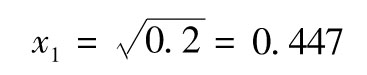 及
及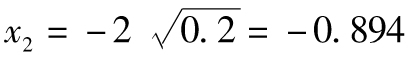 (另外一組解為
(另外一組解為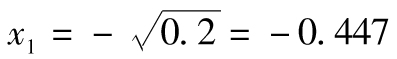 及
及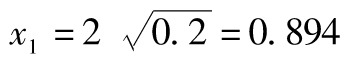 ),向量
),向量
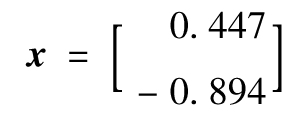
就是對應於特徵值λ=3的特徵向量。
通過一個類似的計算得出,對應於λ=2,式(H-1)為x1+x2=0,滿足以上方程,並且長度為1的向量為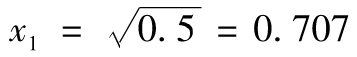 及
及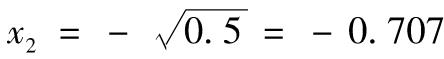 (另外一組解為
(另外一組解為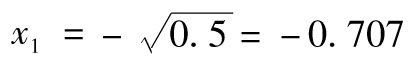 及
及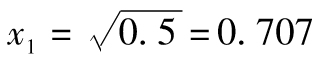 ),向量
),向量
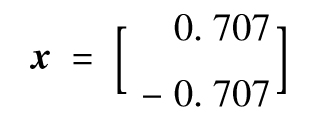
就是對應於特徵值λ=2的特徵向量。對於大型矩陣,我們必須採用數值分析方法來確定特徵值和特徵向量,一種數值方法是由Press等(2007)提供的。[1]
附錄I和附錄J是關於特徵值和特徵向量的應用,計算特徵值和特徵向量的軟件在作者的網站上。
[1] See W. H. Press, S. A. Teukolsky, W. T. Vetterling, and B. P. Flannery, Numerical Recipes: The Art of Scientific Computing, 3rd ed. (Cambridge, UK: Cambridge University Press, 2007).