e1 John Hull 風險管理與金融機構 v5
附錄E
歐式期權定價
對於一個不提供中間收入的資產的歐式看漲期權及歐式看跌期權,布萊克-斯科爾斯-默頓定價公式為
c=S0N(d1)-Ke-rTN(d2)
及
p=Ke-rTN(-d2)-S0N(-d1)
其中
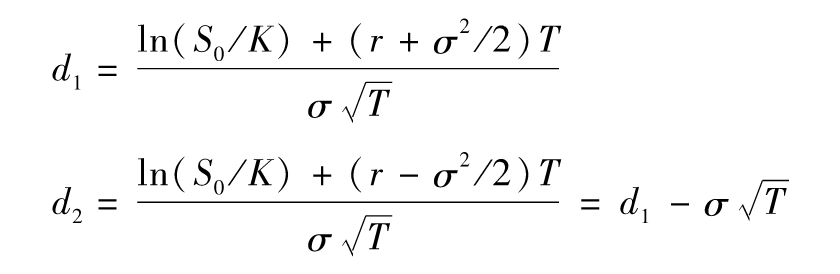
其中N(x)為正態分佈的累積分佈函數(函數表列於本書最後或Excel裡的NORMSDIST功能),變量c及p分別代表歐式看漲期權及歐式看跌期權的價格,S0為在時間0的股票價格,K為執行價格,r為連續複利的無風險利率,σ為股票波動率,T為期權的到期期限。
當資產提供現金收入時,在期權期限內的現金收入的貼現值應該在S0中扣除,當資產提供收入的收益率為q時,以上公式變為
c=S0e-qTN(d1)-Ke-rTN(d2)
及
p=Ke-rTN(-d2)-S0e-qTN(-d1)
其中
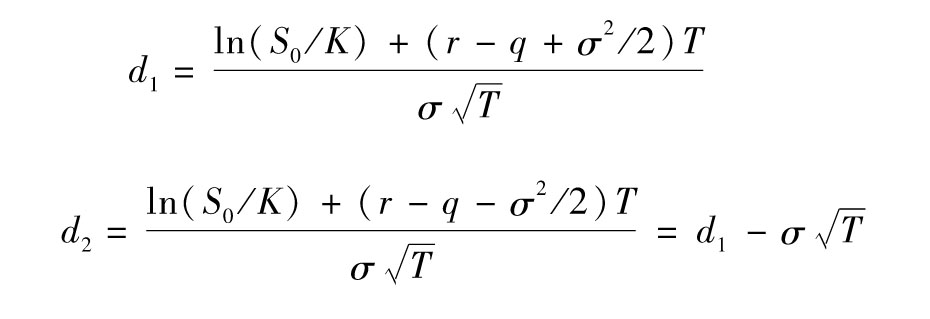
對於匯率期權可以通過設定q等於外匯無風險利率來估值。對於遠期或期貨期權,我們可以採用以上公式,其中,S0等於遠期或期貨的現值,σ是遠期或者期貨價格的波動率。
表E-1給出了期權所對應的希臘值,N′(x)代表正態分佈密度函數,其公式為
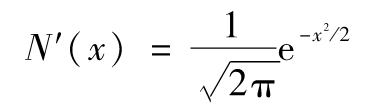
期權的隱含波動率的定義為使得布萊克-斯科爾斯-默頓模型給出的期權價格等於市場價格的波動性(見第10.2節),即σ為隱含波動率。
表E-1 資產的收益率為q的期權的希臘值
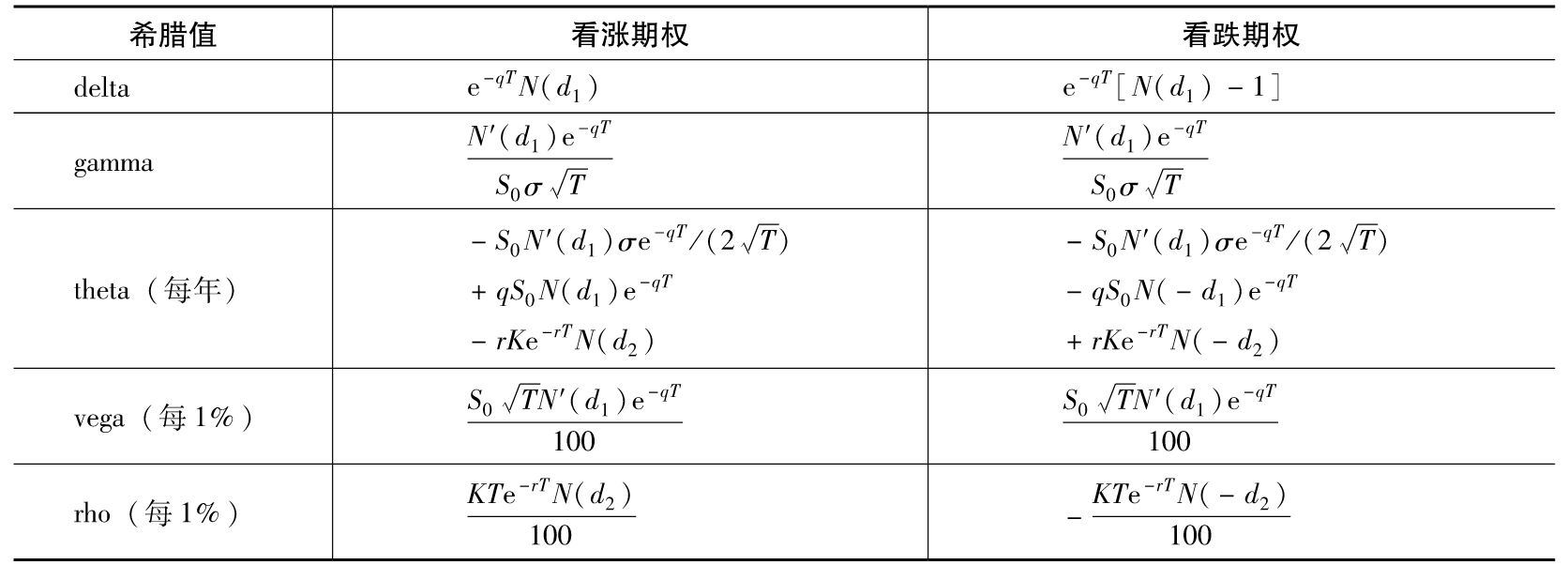
【例E-1】 我們考慮一個6個月期的歐式股指期權,股指的當前價格為1 200,期權執行價格為1 250,無風險利率為5%。股指的股息率為2%,股指的波動率為0.2,這時S0=1 200,K=1 250,r=0.05,q=0.02,σ=0.2,T=0.5,期權價格為53.44,期權的delta為0.45,gamma為0.002 3,theta為-0.22,vega為3.33,rho為2.44,注意表E-1給出的theta的時間單位為每年,我們這裡計算出的theta對應於日曆天。
以上計算可以用RMFI軟件實現,這一軟件可在作者的網頁上下載,在計算中選擇“期權類型:布萊克-斯科爾斯歐式期權”(Option Type:Black-Scholes European),在赫爾(2018)的著作中有關於期權定價更詳細的描述。[1]
[1] See J. C. Hull, Options, Futures, and Other Derivatives, 10th ed. (Upper Saddle River, NJ: Pearson, 2018).