e1 John Hull 風險管理與金融機構 v5

25.4　標準產品的模型

如果某些產品在市場上交易活躍，我們就不需要採用模型來對這些產品定價，市場交易價格就是實際價格。假設市場上某種交易活躍的股指期權，做市商報出的買入價為30美元，賣出價為30.5美元。我們對這一期權的最佳估價為其中間價30.25美元。

場外交易市場一種普遍的情況是儘管被定價的產品是一種標準產品（比如期權），但該產品與市場交易的產品並不完全相同。例如，被定價產品是一種期權，但其執行價格或者期限（或者兩者）與市場上可以直接觀察到的期權有所不同。此時模型被用來保證該產品的定價方式與市場上可觀察到的類似產品的價格一致。布萊克-斯科爾斯-默頓模型在實際中的應用方式為我們提供了一個很好實例（關於布萊克-斯科爾斯-默頓模型，見附錄E）。

布萊克-斯科爾斯-默頓模型之所以有效，是因為它的所有輸入參數（除了一個參數以外）都已知，模型中唯一一個不能被觀察到的變量即是波動率，這意味著價格和波動之間存在一對一的對應關係。當指定了期權的波動率時，就可以計算價格。同樣，如果市場上存在該資產的期權，就可以確定與市場價格相符的波動率。與期權價格保持一致的資產波動率被稱為隱含波動率（implied volatility）。負責對某一特定資產進行投資的交易員會跟蹤所謂的波動率曲面，這一曲面顯示了期權波動率同期權執行價格以及期限的函數關係。

表25-1顯示了一個匯率期權的波動率曲面（為簡單起見，我們假設當前匯率接近1）。注意，如果布萊克-斯科爾斯-默頓模型確實是對市場假設的一個準確描述的話，那麼表中的波動率應該為常數，不會隨時間而變化。針對不同的執行價格和期限，期權的隱含波動率是不一樣的，並且它們會隨著時間而變化（對於所有資產的期權都是如此）。交易員的工作是瞭解當前的波動率曲面以及其隨時間的變化情況。

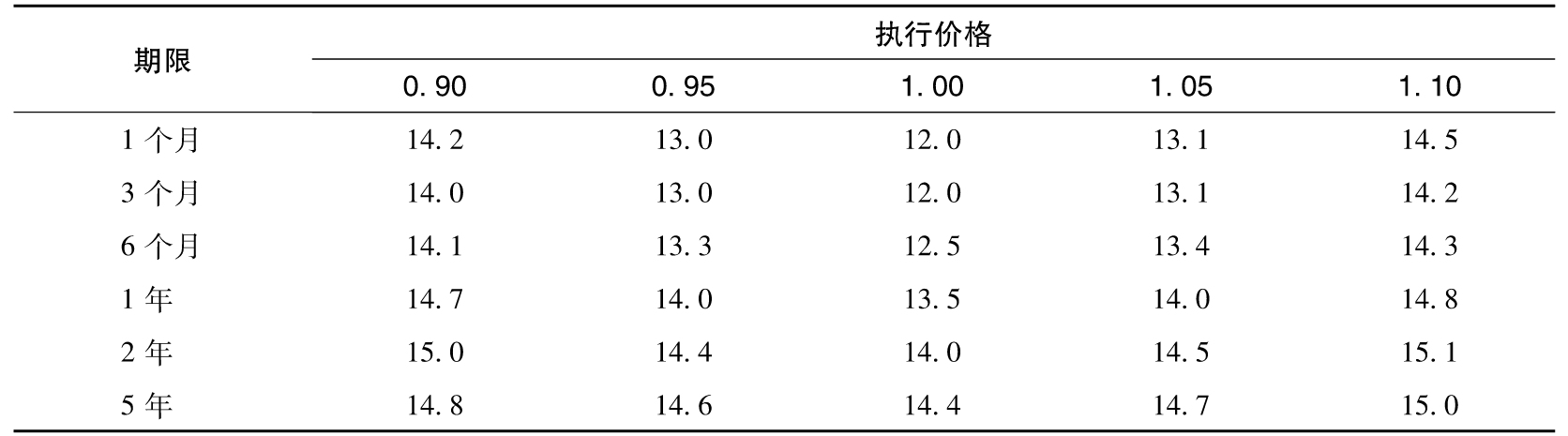
注：不同執行價格和期限的波動率以年百分比的形式給出。

假設某交易員想要為一個9個月期限和執行價格為1.05的期權進行定價（見表25-1）。具有此行權價的6個月期限的期權的波動率為13.4%，1年期限的期權的波動率為14.0%。交易員可以對13.4%及14.0%進行插值，作為對波動率估計，插值結果為13.7%。這一數據可以用於布萊克-斯科爾斯-默頓模型，從而評估波動率為13.7%的期權的價值。假設期限和執行價格都與表中不同，我們可採用二維插值。首先在執行價格之間插入，然後在期限之間插入（如果先在到期期限之間插值，然後在執行價格之間插值，也會得到相同的答案。見練習題25.12）。考慮執行價格為0.92和期限為1.5年的期權。具有此行權價的1年期限的期權的插值隱含波動率為14.42%，2年期限的期權的插值波動率為14.76%，因此1.5年期權的插值波動率為14.59%。

25.4.1　標準產品的模型風險來源

模型驗證組面臨的一個問題是，對活躍交易產品價格的確定是否取決於所使用的模型。如果在剛剛考慮的例子中，我們用另一個模型代替布萊克-斯科爾斯-默頓模型，價格會是相似的嗎？這個問題的答案是，當被估值產品的性質與活躍交易的產品完全相同時（即只有執行價格和期限等參數不同），該模型通常不會對價格產生實質性影響。^[1]這是因為這個模型僅僅被用作一個複雜的插值工具，如果另一種合理的模型使用的方式類似於布萊克-斯科爾斯-默頓模型，那麼兩個不同的模型通常會給出相似的交易活躍產品價格。

在極端情況下容易產生模型風險，模型驗證組應該對此進行檢查。例如，當波動率曲面在執行價格或期限維度上非常陡峭時，應該檢查不同模型的運行情況。此外，模型驗證組應該檢查市場上可用的定價數據的可靠性，以及當可用數據比通常少時模型如何工作。

25.4.2　對衝

對於交易活躍的產品，主要的模型風險是對衝。正如我們所討論的，使用不同的模型通常不會對價格產生太大的影響，但會對對衝業績產生影響。

我們應該區分模型內對衝（within-model hedging）以及模型外對衝（outside-model hedging）。模型內對衝是指對模型內已假設具有不確定性的變量來進行對衝，模型外對衝是指對在模型內被假設為常量（或者非隨機變量）的變量來進行對衝。以布萊克-斯科爾斯-默頓模型為例，採用該模型對股票價格的變化進行對衝（delta及gamma對衝）是模型內對衝，這是因為模型假定標的資產價格變化具有不確定性，但是對波動率對衝（vega對衝）是模型外對衝，這是因為模型本身假定波動率為常數。

在實踐中，交易員幾乎總會同時進行模型外對衝和模型內對衝。如我們以前的解釋，這樣做的原因是在參數校正過程中，波動率（在模型中被假設為常數）等參數每天都會發生變化。一個好的交易員在對交易賬戶的風險進行監控時，會關心交易賬戶對於市場常見的波動率曲面移動的敏感性。^[2]

如果一個模型給出的產品價格與市場價格一致，並且對每天會產生變化的變量都進行對衝（這裡的參數包括模型中假設的常量以及隨機變量），那麼理論上對衝後會使交易員頭寸的價值保持恆定。事實上，這並不一定成立。再次考慮布萊克-斯科爾斯-默頓模型來評估匯率期權中的頭寸價值。每個期權價格都是匯率、其隱含波動率和期限的確定性函數，^[3]這意味著交易員對投資組合中所有期權的匯率和隱含波動率都有風險敞口。通過外匯交易，可以很容易地對衝匯率風險，這被稱為delta對衝，通常至少進行一次（參見第8章）。對衝波動率變化的風險並不那麼容易，這需要在其他期權（可能是昂貴的）上進行交易，並且基於波動率曲面會隨時間變化的假設。^[4]因此，波動率對衝不可能像delta對衝那樣有效。

在實踐中，delta對衝往往是交易員唯一定期進行的對衝。期權頭寸的delta取決於所使用的模型，這意味著交易員採取的對衝頭寸因模型而異。模型驗證組的一項重要工作是測試用於替代模型的delta對衝的有效性。

25.4.3　損益分解

可以進行的一種分析稱為損益分解（P&L decomposition）。風險經理將投資組合每天價格的變化分解成以下成分：

（1）沒有被對衝的風險所帶來的變化；

（2）由於對衝模型的不完善所帶來的變化；

（3）每一天新的交易所帶來的變化。

如果某天價格變化變得不可接受，損益分析就會指出在哪些方面我們應花更多精力。好消息是，平均來講，根據錯誤模型進行對衝導致總損失或總收益通常很小，這是因為在一家較大的金融機構中，不完美對衝所帶來的風險通常會被不同的交易組合分散。

[1] 這在S. Figlewski, “Assessing the Incremental Value of Option Pricing Theory Relative to an Informationally Passive Benchmark,” Journal of Derivatives (Fall 2002):80-96中已經說明。

[2] 我們可以採用第9章描述的主成分分析方法。如果風險敞口對每個主要成分的敏感性都很小，則敞口對實際中觀察的移動的敏感性也會很小。

[3] 為簡化例子，假設利率和股息收益率恆定。

[4] 如果可以完全對衝波動率曲面的波動，那麼delta對衝的差異將被波動率對衝的差異所抵消，但這在實踐中並不能完美實現。