e1 John Hull 風險管理與金融機構 v5
14.4 對於期限結構的處理
期限結構描述了利率、信用價差和平價波動率等變量。期限結構表明這些變量的值是到期期限的函數。當變量為利率時,期限結構顯示零息利率與其到期期限的關係(有關如何計算零息利率的討論,請參見附錄B)。當變量為信用價差時,期限結構反映了適用於債券或信用違約互換的信用價差與其到期期限的函數關係。當變量為平價波動率時,期限結構顯示了平價期權定價的波動率是其到期期限的函數。[1]
期限結構使模型構建方法更復雜。例如,考慮特定利率的期限結構。公司投資組合中的一種工具可能會在3.32年內產生現金流量,在接下來的短時間內,這一工具的價值變化取決於期限結構上3.32年到期點的情況;另一種工具可能會在4.48年的時點上產生現金流,因此金融機構在期限結構上的該時點也會有風險敞口。3.32年期利率和4.48年期利率將趨於一致,但二者並非完全相關。
顯然,我們不可能對這家金融機構每一種期限的工具都加以考慮。我們將考慮兩種處理期限結構風險的方法:主成分分析和“多重頂點法”(multiple-vertices approach)。對於股票價格、價格和匯率等變量,若變量的值成百分比變化,那麼參數σ就是百分比變化的標準差(如波動率)。在介紹的這兩種方法中,對於這些變量,我們通常考慮實際變化,而不是百分比變化。
14.4.1 主成分分析法
我們在第9.7節中討論了主成分分析法(PCA)的性質。前兩個或三個主因子(PC)說明了在實踐中觀察到的期限結構的大部分變化。第一個因子通常是期限結構的平行移動;第二個因子是期限結構斜率的變化;第三個因子是“彎曲”,即存在期限結構的曲率變化。
處理期限結構的一種方法是,假定1天之內期限結構的變化僅由前兩個或三個主因子引起。我們使用第9章中利率敏感性的例子來說明計算方法。表14-6中的數據是投資組合對利率變動的敏感性。因子載荷和因子得分的標準差在表14-7和表14-8中列出(與表9-6和表9-7相同)。
表14-6 利率1個基點變動所觸發的投資組合價值(以百萬美元計)的變化

表14-7 互換利率的因子載荷
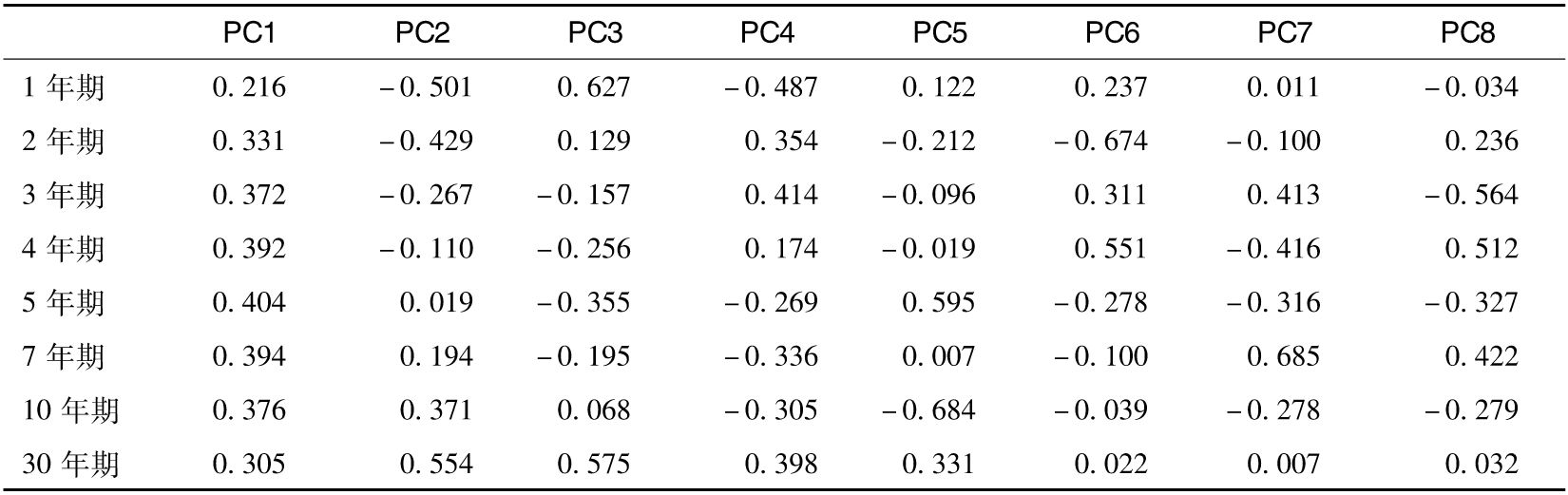
假設前兩個主因子描述了利率變動。投資組合對第1個主因子的敏感度敞口是
10×0.372+4×0.392-8×0.404-7×0.394+2×0.376=+0.05
對第2個主因子的敏感度敞口是
10×(-0.267)+4×(-0.110)-8×0.019-7×0.194+2×0.371=-3.88
均以每個基點的百萬美元為衡量單位。
假設f1和f2是前兩個主因子的因子得分,我們將它們視為每日變化的第一主因子和第二主因子的個數。前兩個主因子導致的投資組合價值在1天之內的變化(以百萬美元計)為
ΔP=0.05f1-3.88f2
主成分分析法中的因子得分相互獨立。表14-8顯示主成分分析法中前兩個因子的標準差分別為17.55和4.77,因此ΔP的標準差為
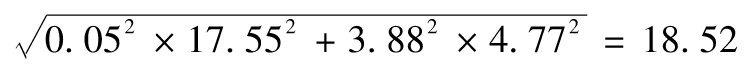
表14-8 因子得分的標準差

假定因子得分服從正態分佈,1天展望期的99% VaR等於18.52×2.326=43.08百萬美元,即4 308萬美元。
注意投資組合對於第1個因子的敏感性較低,而對於第2個因子的敏感性較大。只採用第1個因子(見練習題14.9)進行計算會顯著地低估VaR。
剛才考慮的示例僅對因子載荷表(見表9-7)中的期限有敏感性敞口,可使用內插法計算其他到期期限的敏感性敞口。例如,假設3.5年利率的第1個因子敞口為0.382,第2個因子敞口為-0.188 5,依此類推。
14.4.2 多重頂點法
在度量風險敞口時,衍生工具交易商及其監管者喜歡引入期限結構。我們再次通過利率期限結構來闡述這一點。假設利率期限結構由不同到期期限對應的點構成:3個月、6個月、1年、2年、3年、5年、10年、15年、20年和30年。期限結構是連接這些點的分段線性曲線,如附錄B中所述。通過將一個點移動一個基點,同時保持其他點不變,可以為期限結構上的每個點計算一個delta。我們將以這種方式定義的delta稱為“節點delta”(node delta,使用第9章的術語,又叫“現金局部久期”)。圖14-1顯示了計算5年節點delta時的期限結構變化。其他時點的delta也是類似的計算。當計算最短到期期限(3個月)的delta時,所有小於這一時點的利率都增加一個基點;當計算相對於最長期限(30年)的delta時,所有大於最長期限的利率都增加一個基點(這與附錄B中描述的期限結構的構造方法是一致的)。節點delta的總和為DV01(這是整個期限結構中每個時點的利率平移一個基點的影響)。因此,節點delta是將DV01分為10個組成部分的一種方式。
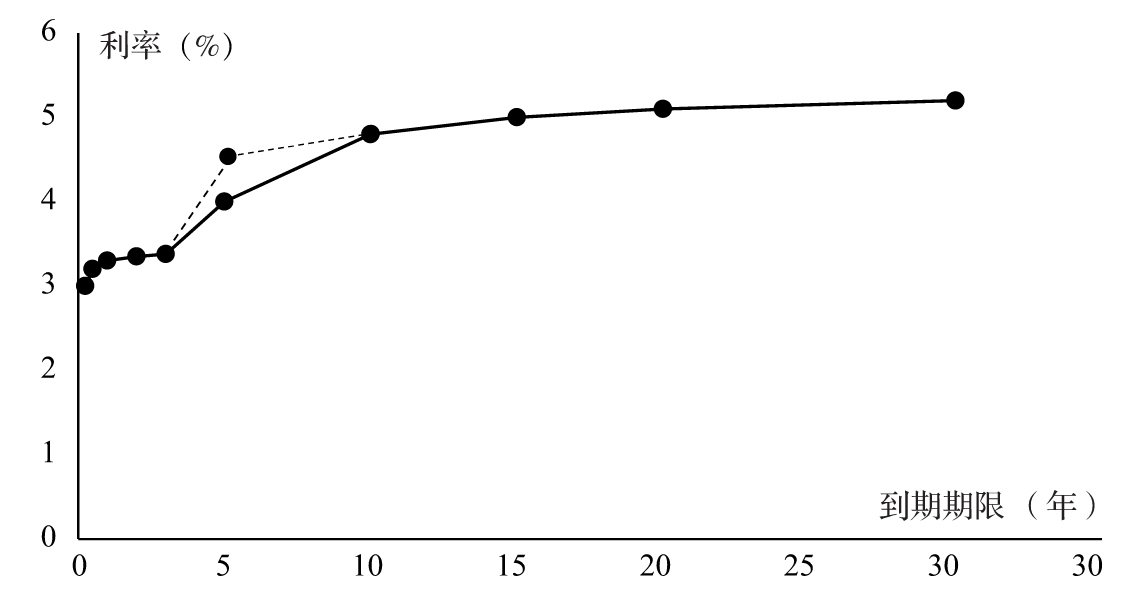
圖14-1 5年期利率隨其他利率不變的變化
考慮一個投資組合,其價值僅取決於一個期限結構。將δi定義為第i個節點delta(當第i個到期期限的利率上升一個基點時,投資組合的價值增加值)。如果σi是第i個節點相對應的1天的利率變化的標準差(以基點為單位),ρij是第i個節點和第j個節點的利率變動之間的相關性,則投資組合在1天之內價值變化的標準差是

任何給定的未來現金流量都具有相對於兩個相鄰到期日的delta。例如,3.5年的現金流相對於3年期利率和5年期利率具有delta,而相對於其他利率則沒有。如果3.5年期利率的一個基點變化的影響為X,那麼3年節點的delta為0.75X,5年節點的delta為0.25X。
注意,式(14-4)與式(14-2)相同。唯一不同的是,式(14-2)考察風險因子的百分比變化(δ變量衡量百分比變化的風險因子對投資組合的影響,σ變量是波動率),而式(14-4)考察風險因子的實際變化(δ變量衡量風險因子實際變化的影響,而σ變量是標準偏差)。式(14-2)和式(14-4)可以擴展到一個考慮某些風險因子的百分比變化和考慮其他風險因子的實際變化的投資組合。
現在假設投資組合P的價值取決於K個期限結構。定義δik、σik、ρijk分別是期限結構k(1≤k≤K)中δi、σi、ρij的值,同時定義
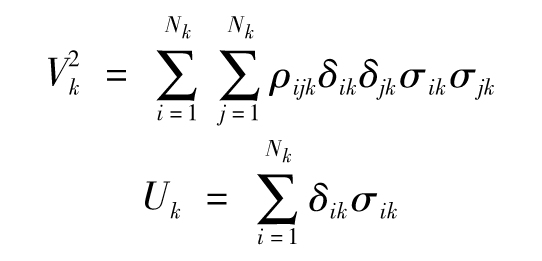
其中Nk是用於期限結構k的頂點數。
通常用一個參數描述兩個期限結構之間的相關性。假設ρ(k1,k2)是期限結構k1和k2之間的相關性。定義它的兩種方法如下:
(1)對於所有i和j,期限結構k1的利率i與期限結構k2的利率j之間的相關性是ρ(k1,k2)。
(2)由於期限結構k1和期限結構k2的變動而導致的投資組合價值的變化之間具有ρ(k1,k2)的相關性。
根據第一個定義可以得到
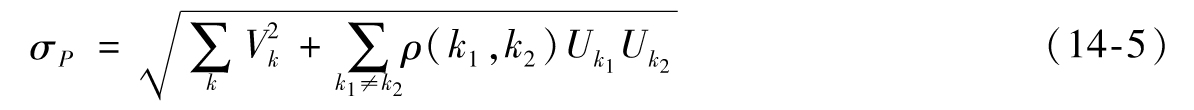
根據第二個定義可以得到
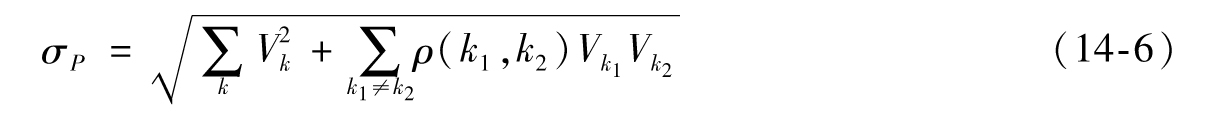
【例14-2】 假設一個投資組合有兩種不同的利率期限結構敞口。表14-9顯示了每天利率變動的標準差以及利率變動的delta敞口。例如,期限結構1的2年期利率每天變化的標準差為5.6個基點(0.056%),而期限結構2的2年期利率每天變化的標準差為11.4個基點。2年期利率的一個基點變化對於期限結構1的影響是8500萬美元,對於期限結構2是6500萬美元。假設兩個期限結構中各節點的相關性ρij都相同,如表14-10所示。期限結構1中的1年期利率變動與期限結構1中的2年期利率變動之間的相關性為0.92。期限結構2也是如此。
表14-9 標準差(以基點為單位)和delta敞口(以每個基點百萬美元計)
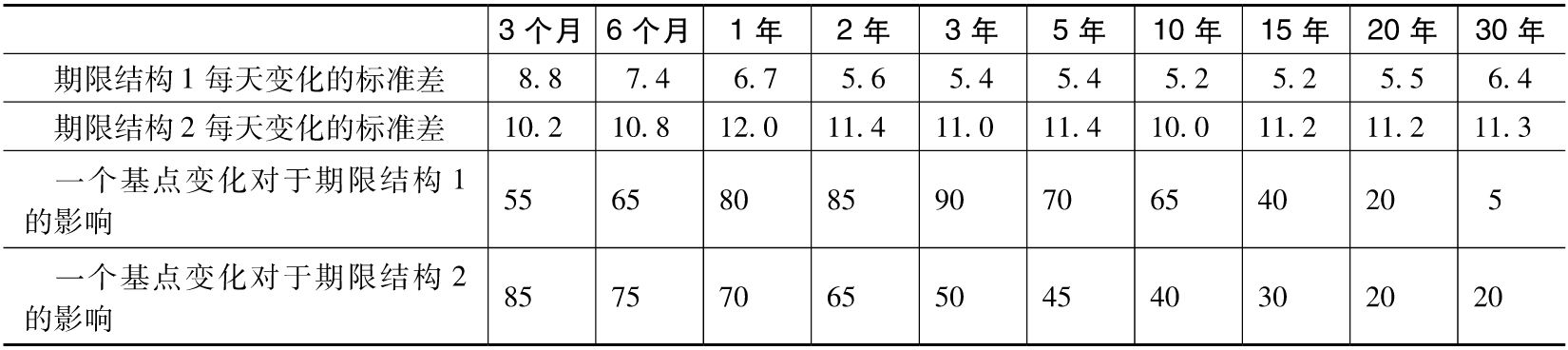
表14-10 不同期限利率之間的相關性
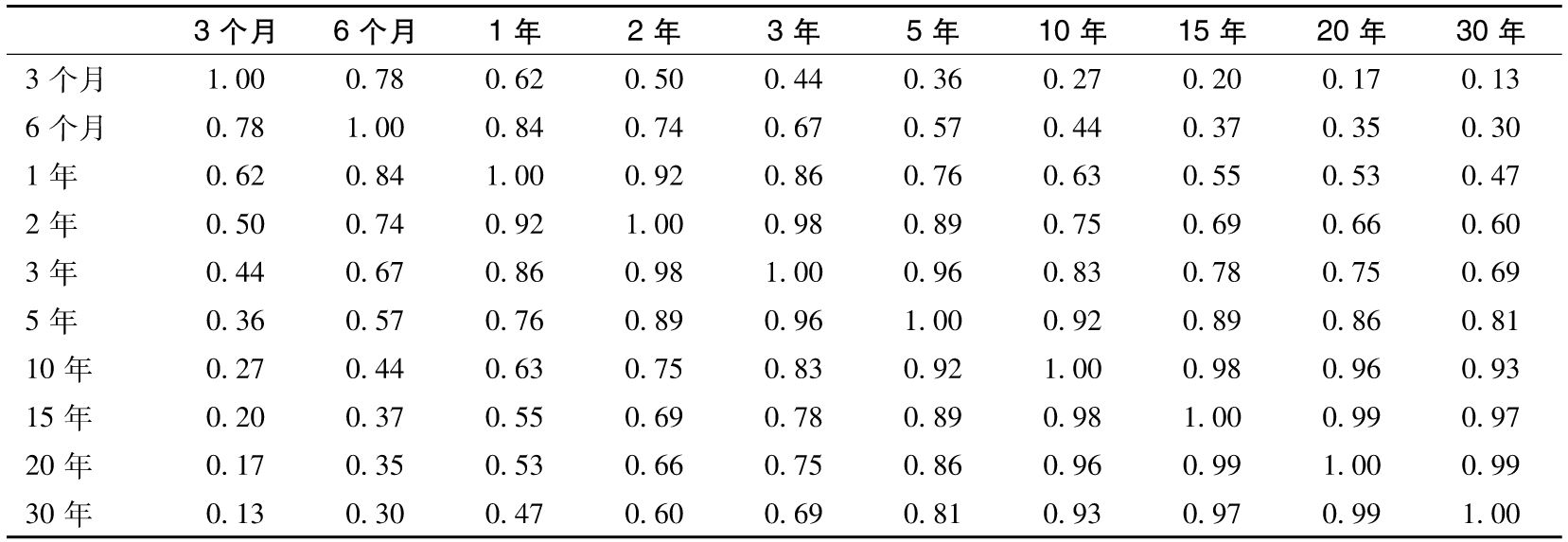
最後,我們假設兩個期限結構之間的相關參數為0.4(以百萬美元計),結果是
U1=3 529 U2=5 501
V1=3 004.9 V2=4 604.3
式(14-5)給出的每天投資組合標準差為6 163.9,式(14-6)給出的每天投資組合標準差為5 980.2。將它們乘以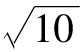 和2.326得到10天的99%VaR。使用式(12-2)計算ES。計算結果顯示在作者的網站上:www-2.rotman.utoronto.ca/~hull/riskman。
和2.326得到10天的99%VaR。使用式(12-2)計算ES。計算結果顯示在作者的網站上:www-2.rotman.utoronto.ca/~hull/riskman。
[1] 正如我們稍後將解釋的那樣,普通期權價格與波動率近似線性相關,因此可以使用式(14-2)處理其對波動率的依賴關係。