e1 John Hull 風險管理與金融機構 v5

14.1　基本方法論

我們先考慮當投資組合只包含單一股票時如何用模型構建法來計算VaR。假定投資組合只包含價值為1000萬美元的微軟公司股票，在計算中我們選擇10天的展望期，同時假定置信水平為99%，在這裡我們要求出投資組合在10天展望期內、99%置信水平下，損失不能超出的數量。在計算過程中我們首先將展望期選定為1天。

我們假定微軟公司股票的波動率為每天2%（對應於每年的波動率32%），^[1]交易頭寸的數量為1 000萬美元，投資組合每天價值變化的標準差為1 000萬美元的2%，即200 000美元。

在模型構建法中，我們往往需要假定在展望期內，市場價格變化的期望值為0，這一假設雖然不是絕對正確的，但也還算合理。同標準差相比，市場變量在一個較小的時間區間內價格變化的期望值相對較小。例如，微軟公司的年回報大約是20%，以1天為計，預期回報大約是0.20/252，約等於0.08%，與此對應的每天價格變化的標準差大約為2%。考慮10天的展望期，預期回報大約為0.08％×10，即0.8%，而10天所對應的回報標準差為，即6.3%。

截至目前，我們得出微軟公司股票每天價格變化的標準差為200 000美元，並且（以近似意義來講）每天價格變化的均值為0。我們假定價格的變化服從正態分佈。^[2]因為N（-2.326）=0.01，所以我們得出在正態分佈下，價格下降大於2.326倍的標準差的概率為1%。另外一種等價的說法是，在正態分佈下，我們有99%的把握肯定價格下降程度不會超過2.326倍的標準差，因此，我們得出1 000萬美元微軟公司股票1天展望期的99%的VaR等於

2.326×200 000=465300（美元）

假定微軟公司股票連續每天之間變化相互獨立，我們可以假設10天的收益率標準差為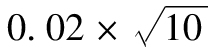，10天的收益率為正態分佈，因此微軟公司10天的99%的VaR等於

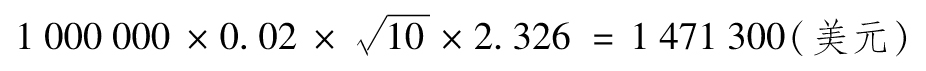
10天的99%的ES可由式（12-2）計算得出，令，Y=2.326，且X=0.99。ES的值為1 687 000美元。

接下來我們考慮價值為500萬美元的AT&T的股票投資。假定AT&T的每天價格波動率為1%（這對應於每年16%），採用與微軟公司股票類似的計算，我們得出AT&T的每天價格變化的標準差為

5 000 000×0.01=50000

假定價格的變化為正態分佈，1天展望期的99%的VaR等於

50 000×2.326=116 300（美元）

10天展望期的99%的VaR等於

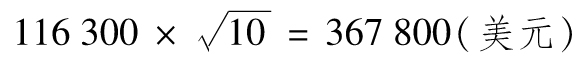
由式（12-2），10天展望期的99%的ES為421 400美元。

14.1.1　兩個資產的情形

接下來我們考慮價值為1 000萬美元的微軟公司股票和價值為500萬美元的AT&T股票的投資組合。我們假定微軟公司及AT&T的股票價值變化服從二元正態分佈，分佈中的相關係數為0.3。由統計學中一個標準的結果得出，如果變量X和Y的方差分別為σ_X和σ_Y，變量的相關係數為ρ，那麼X+Y的標準差為

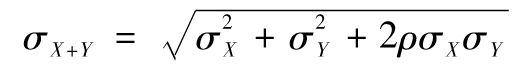
在應用這一結果時，我們令X為微軟公司股票每天的價格變化，令Y為AT&T股票每天的價格變化

σ_X=200 000，　σ_Y=50 000

因此，由兩種股票所組成的投資組合價值的1天變化的標準差為

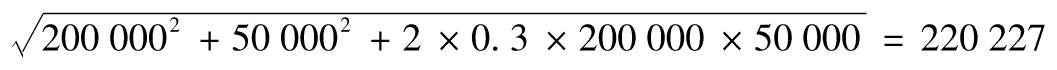
投資組合價值變化的期望值為0，如果我們進一步假設微軟公司和AT&T的收益的聯合分佈是雙變量正態分佈，那麼投資組合的價值變化服從正態分佈。我們得出1天展望期的99%的VaR等於

220 227×2.326=512 300（美元）

考慮10天展望期，σ_X和σ_Y增加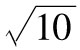倍，則10天展望期的99%的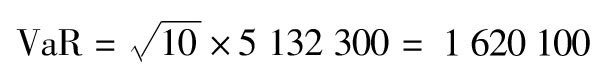美元。由式（12-2），10天展望期的99%的ES為1 856 100美元，其中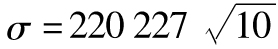，Y=2.326，X=0.99。

14.1.2　風險分散的益處

我們以上考慮的例子滿足以下性質：

（1）由單一微軟公司股票組成的投資組合的10天展望期的99%的VaR等於1 471 300美元。

（2）由單一AT&T股票組成的投資組合10天展望期的99%的VaR等於367 800美元。

（3）由微軟公司及AT&T兩種股票組成的投資組合的10天展望期的99%的VaR等於1 620 100美元。

數量（1 471 300+367 800）-1 620 100=219 000美元代表風險分散帶來的好處。如果微軟公司及AT&T的相關係數等於1（完全相關），由微軟公司及AT&T共同組成的投資組合的VaR等於單一微軟公司組合的VaR加上單一AT&T組合的VaR；如果相關係數小於1，就會帶來部分風險的分散化解（diversified away）。^[3]同樣的結論對ES也適用。

[1] 如第10.1節所示，在計算VaR時，波動率通常以每天為計量，而在期權定價時，通常以每年為計量，我們可以將每天波動率乘以，即大約為16，轉化為每年的波動率。

[2] 我們可以假定微軟公司股票價格在明天的分佈為對數正態（lognormal），因為1天展望期的時間太短，在這裡對數正態假設與我們以前所做的連續兩天的股價變化服從正態分佈的假設幾乎沒有什麼區別。

[3] 如第12.5節所示，VaR並不一定永遠能帶來風險分散效應。對於非正態分佈，兩個交易組合在合併後所產生的VaR可能會大於兩個交易組合的VaR的總和，而ES沒有此缺點。