e1 John Hull 風險管理與金融機構 v5

13.3　歷史模擬法的擴展

對非壓力VaR和ES使用歷史模擬法計算的一個關鍵假設是歷史在某種意義上是對將來的一種指導。更為準確地講，即假設由過去幾年數據得出的關於市場變量的實證概率分佈，是對明天市場變量行為的一個指導。不幸的是，市場變量的行為並非平穩的，有時市場波動率會很高，有時會很低。在這一節中，我們將提出第13.1節中的基本歷史模擬法的幾種拓展方法，這些拓展的目的是對歷史數據非穩態的情況進行調整。我們還會介紹一種被稱作自助法的統計方法，該方法可用來確定標準誤差。

13.3.1　對觀察值賦權

在最基本的歷史模擬法中，過去每一天觀察值所對應的權重都相等。更精確地講，當我們採集了n天的日價格變化數據後，我們對於這n個觀察值中任意一個所設定的權重均為1/n。Boudoukh（1998）等建議，對最近的觀察數據應該賦予更大的權重，這可以保證模型充分反映當前市場波動率以及當前市場經濟環境的變化。^[1]一種較為自然的權重選擇是使得觀測值的權重隨時間回望期的延伸而呈指數遞減（在第10章中介紹指數加權平均移動模型時，我們曾經對這一方法進行過討論）。情景1所對應的權重（對應於最遙遠的數據）等於λ乘以情景2的權重，情景2所對應的權重等於λ乘以情景3的權重，依此類推。所有權重之和為1，情景i所對應的權重為

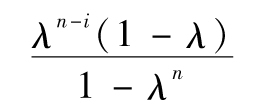
其中n為觀察值的天數。當λ趨向於1時，這一權重趨向於基本歷史模擬法的權重，也就是說權重趨向於1/n（見練習題13.2）。

將所有的觀察值由最壞到最好進行排序，我們可以計算出VaR。由損失最壞的情景開始，我們開始累積計算每一項權重的和，當權重總和達到某指定的分位數界限時，停止計算。例如，假定我們需要計算置信程度為99%的VaR，將觀察數據排序後，我們由最壞的損失開始計算權重和，當權重和剛好超過0.01時，我們停止計算。這時所對應的損失恰恰是置信程度為99%的VaR。對於最佳參數λ的選取，我們可以通過實驗不同的λ，並選擇在回顧檢驗中表現最佳的。與一般的歷史模擬法相比，指數加權方法的缺點在於其應用的有效抽樣的數量較小，但採用一個較大的n是對這一缺陷的補救。事實上，隨著時間的推移，我們並不需要捨棄那些較為陳舊的數據，因此它們對應的權重很低。

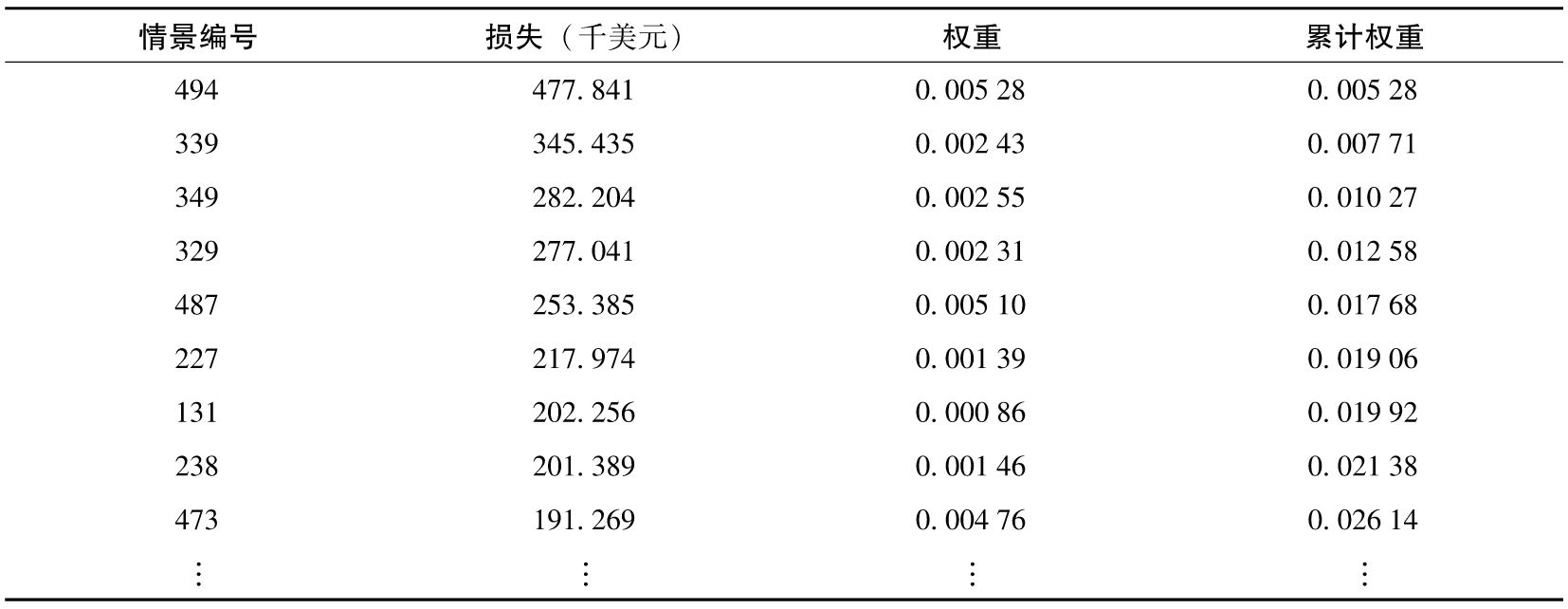
表13-5顯示了將這一方法應用到第13.1節中討論的組合所得出的結果，其中λ=0.995（參見作者網站上給出的表單文件中的工作表4和工作表5）。當置信程度為99%時，VaR對應於第3個最糟糕的情景，即282 204美元（而不是第5個最糟情景，即253 385美元），原因是最近的觀察值對應較高的權重，而最大損失的發生時間相對較近。第13.1節的標準計算對所有的觀察值設定的權重為1/500=0.002。最大損失對應於情景494，這一情景所對應的權重為

在損失分佈0.01的尾部中，有0.005 28的概率損失477 841美元，0.002 43的概率損失345 435美元，有0.01-0.005 28-0.002 43=0.002 28的概率損失282 204美元。因此，ES的計算如下

13.3.2　在歷史模擬法中進行波動率的更新

Hull和White（1998）提出了一種在歷史模擬法中引入波動率估計的方法。^[2]假定在第i-1天結束時，對於某市場變量的波動率估計為σ_i，這一數值可以被認為是對第i-1天天末和第i天天末之間的波動率的估計。假定現在為第n天天末，對於市場變量的當前波動率（即今明兩天之間的波動率）估計為σ_n+1。

假定對某變量，σ_n+1是σ_i的2倍。這意味著，我們對某市場變量今天的波動率估計為第i-1天的波動率估計的2倍，因此我們預期今天到明天的變化量也應該是從第i-1天到第i天變化量的2倍。在進行歷史模擬分析時，我們試圖由歷史上第i-1天至第i天的變化，得出由今天到明天變化的一個抽樣，很自然地我們應該將第i-1天至第i天的變化乘以2，一般來講，在實施這一想法時，式（13-1）中的市場變量在第i個情景會變成

在模擬過程中，我們對所有的市場變量均可採取同樣的處理方式。

這一方法很自然及直觀地考慮了波動率的變化，VaR的估計值包括了最新的市場信息，這樣計算出的VaR可能會大於當前交易組合對應於歷史上任意一天情景變化而計算出的損失。Hull和White採用匯率及股指數據證明，這一方法的確比傳統歷史模擬法及指數加權方法要好。

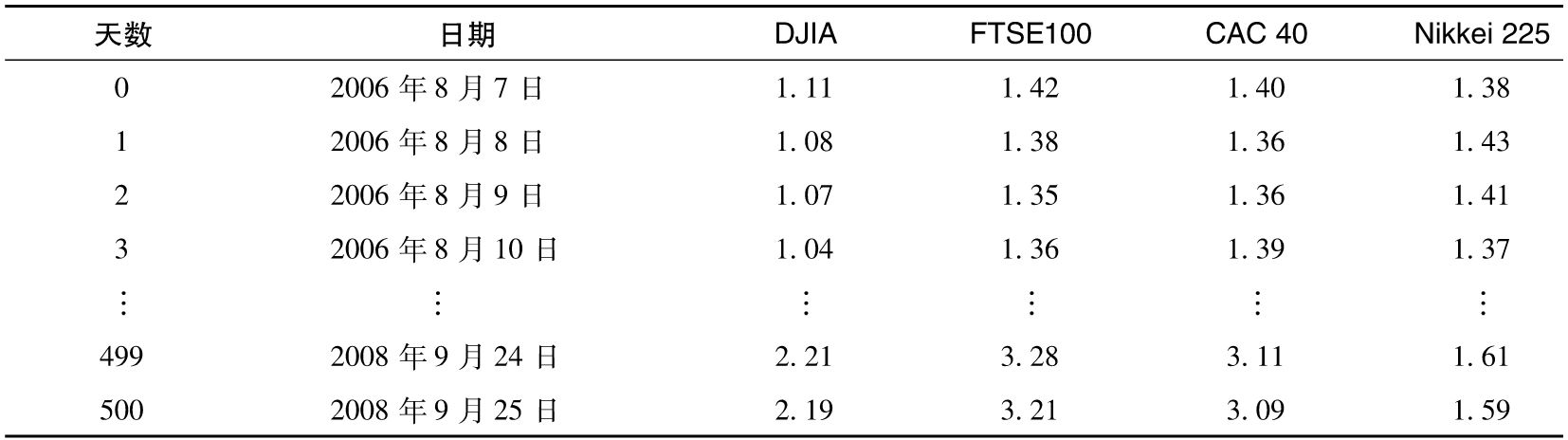
按表13-2中的數據，假定λ=0.94，我們可以使用指數加權移動平均法（EWMA）估計每天的波動率，計算結果被顯示在表13-6中^[3]（見作者網站提供的表單文件中的工作表6～8）。對於DJIA、FTSE 100、CAC 40和Nikkie 225在2008年9月26日得出的波動率（表中最後一行）與在2008年8月8日得出的波動率（表中第1行）的比率分別為1.98、2.26、2.21、1.15。這些比率作為2006年8月7日～8月8日指數實際變化的乘數因子；類似地，對於以上股票指數，在2008年9月26日得出的波動率（表中最後一行）與在2008年8月9日得出的波動率（表中第2行）的比率分別為2.03、2.33、2.28、1.12，這些比率是作為2006年8月8日～8月9日指數實際變化的乘數因子；其他498天每天變化的乘數因子可以採用類似的方法得出。

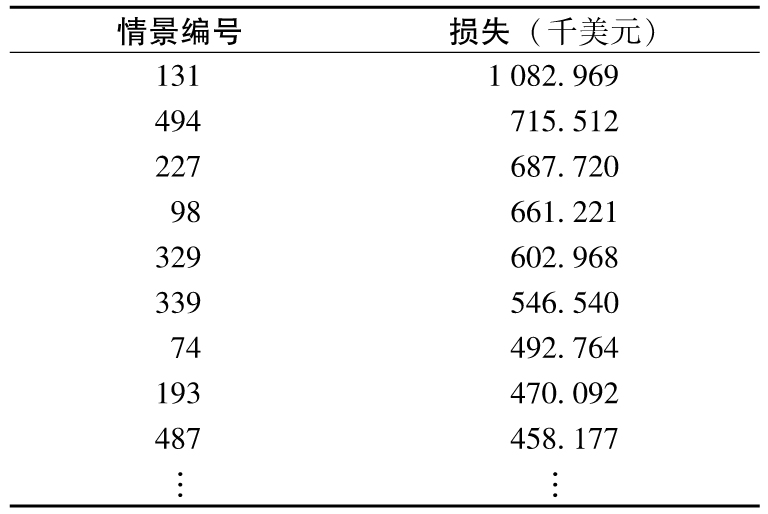
在我們給出的例子中，波動率在歷史數據的結束時達到最高，波動率調整的效果是對500個情景的盈虧增加了變動幅度。表13-7中顯示了將損失由最高到最低進行排序後的部分數據。與表13-4相比，我們看到損失幅度要高得多。1天展望期的99%VaR為602968美元，ES為786855美元。這些值為由標準法計算出的相應值的兩倍多。

在這個特例中，股票市場的波動率在2008年餘下的時段仍然很高，1天內指數變化在5%～10%並不少見。在這種情況下，採用波動率調整的方式來計算VaR和ES比標準方法要更好。

13.3.3　調整波動率的更簡便的方法

對我們剛才介紹的方法的一種簡化是使用指數移動加權法對第13.1節標準法中模擬計算出的連續情景下損失的標準差進行監測。表13-3中的最後一列顯示了損失。在作者網頁提供的表單文件中的工作表9和工作表10給出了相關計算。針對第i個場景的調整後的損失等於由標準法計算出的損失乘以第500個場景（最後一行）的標準差的估計值與第i個場景的標準差的估計值的比率。相比對多個市場變量的波動率進行逐一更新，此方法非常簡潔，並且具有將相關性的變化及波動率的變化隱含考慮在內的優點。表13-8顯示了本例中損失的標準差以及經調整後的損失（與以往相同，第一天損失的方差仍然設為整個500天樣本的方差，EWMA模型使用的λ等於0.94）。我們可以看到，較晚期場景的損失的標準差估計遠遠高於早期場景。場景1，2，3，…中的損失分別被乘以2.203，2.270，2.335，…

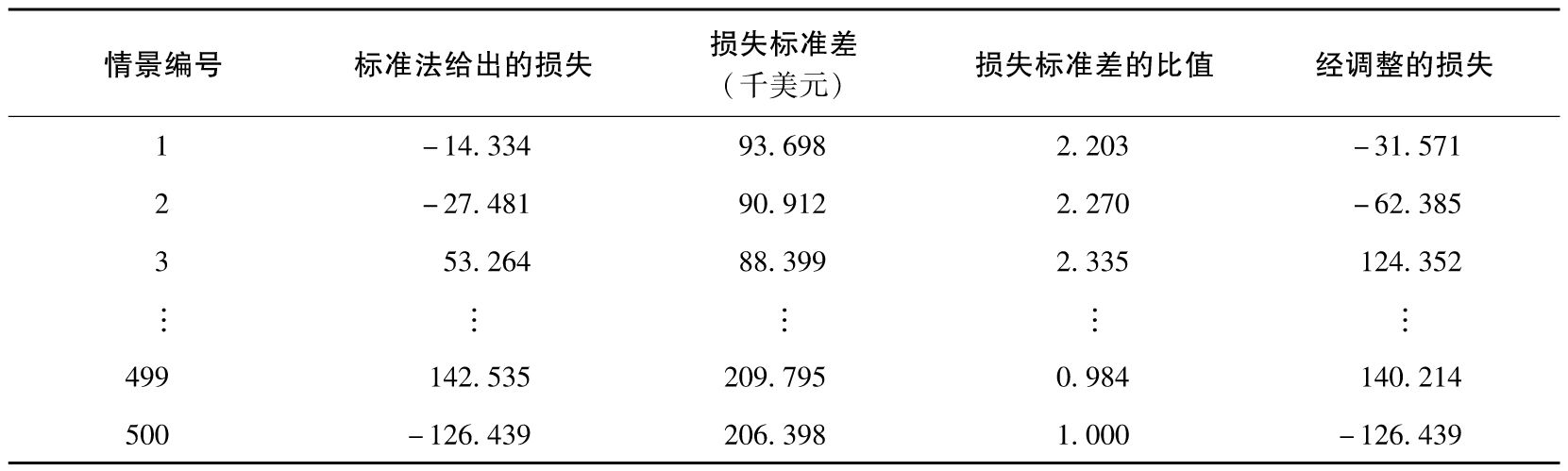
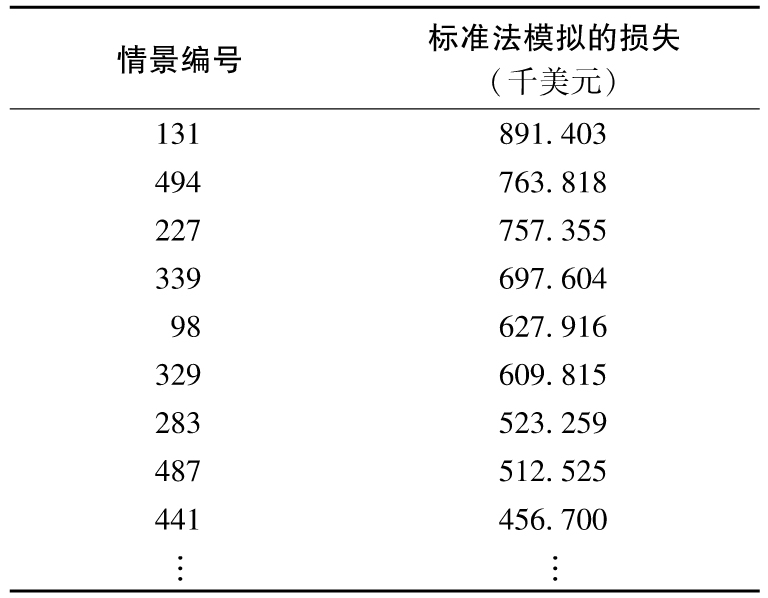
表13-9顯示了經調整後的損失排序後的結果。結果與表13-7中的相似（但得到這裡的結果要簡單得多）。1天展望期的99%置信度的VaR是627 916美元，ES為777 545美元。

13.3.4　自助法

自助法（bootstrap method）是基本歷史模擬法的一種變形，其目的是計算VaR（非壓力VaR或壓力VaR）值本身的置信區間。^[4]在這種方法中，我們首先需要按傳統的手段，以歷史數據的變動為基礎，來計算出交易組合的價值變化，然後我們對變化數據進行放回抽樣（sample with replacement），並由此來產生新的抽樣數據。對每一組新的數據，我們都要計算相應的VaR，95%VaR的置信區間估計恰好是介於由新產生數據所計算出的VaR的分佈中第2.5個分位數及第97.5個分位數所界定的範圍。

例如，假定我們有500個數據，我們可以採用放回抽樣的形式，對數據進行抽樣50萬次，由此我們可以產生1000組500天的數據，對於每一組數據我們可以進行VaR運算，並按從小至大的順序進行排列，假如，名列第25位的VaR值為530萬美元，名列第975位的VaR值為890萬美元，因此對應於95%置信水平的置信區間為530萬～890萬美元。通常來講，由自助法所計算出的置信區間範圍要小於由第13.2節中的方法所給出的範圍。

[1] See J. Boudoukh, M. Richardson, and R. Whitelaw, “The Best of Both Worlds: A Hybrid Approach to Calculating Value at Risk,” Risk 11 (May 1998):64-67.

[2] See J. Hull and A. White, “Incorporating Volatility Updating into the Historical Simulation Method for Value at Risk,” Journal of Risk (Fall 1998):5-19.

[3] 方差序列的初始值取決於我們做出的選擇。我們這裡所採用的初始方差等於整個取樣樣本的方差。

[4] See P. Christoffersen and S. Goncalves, “Estimation Risk in Financial Risk Management,” Journal of Risk 7, no.3(2007):1-28.