e1 John Hull 風險管理與金融機構 v5
10.3 金融變量的每日變化量是否服從正態分佈
當通過波動率來計算市場變量變動的置信區間時,一個常用的假設是市場變量服從正態分佈。這也是在例10-1和例10-2中我們採納的假設。在實際中,大多數金融變量的值發生較大變化的可能性比正態分佈所給出的要大。表10-1顯示了用10種匯率在2005~2015年10年期內的日變化量來檢驗其是否符合正態分佈的結果。這10種匯率分別是美元與下列貨幣之間的匯率:澳元、英鎊、加拿大元、丹麥克朗、歐元、日元、墨西哥比索、新西蘭元、瑞典克朗和瑞士法郎。編制該表的第一步是計算每種匯率的日百分比變化的標準差,第二步是計算有多少百分比變化超過1個標準差、2個標準差,等等。將這些數字與正態分佈上對應的數字進行比較。
表10-1 價格比例變化大於1,2,…,6個標準差的天數佔全部觀察日數的比例(S.D.=價格比率變化的標準差)
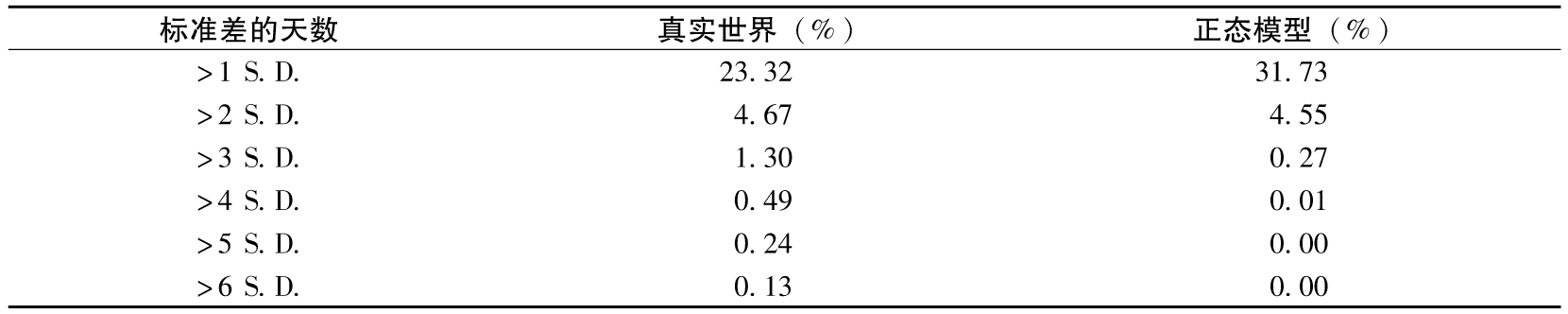
每天價格百分比變化超過3個標準差的個數佔所有觀察數據的比例為1.30%,而正態分佈所對應的比例只是0.27%。每天價格百分比變化超出4個、5個以及6個標準差的天數佔整個觀察日的比例分別為0.49%、0.24%以及0.13%,而正態分佈認為這些事件幾乎不可能發生。因此,表10-1提供了實際中的匯率變化比正態分佈的預測存在更肥大尾部的證據。
當對回報採用連續複利時,多日的回報等於其中每日回報的和。如果每日回報服從相同的非正態概率分佈,那麼統計學上的中心極限定律給出的結論是:多日的回報服從正態分佈。實際上,連續多日的回報並不服從同一個分佈(其中一個原因是,波動率並不為常數。我們會在本章的後面討論這個問題)。因此,較長觀察期內的回報以及每日回報的分佈都會呈現肥大的尾部。業界事例10-2指出,如果你早在1985年做了這一分析,你將如何賺大錢。
業界事例10-2
如何從外匯期權中盈利
布萊克、斯科爾斯和默頓在他們的期權定價模型中假設標的資產的價格在將來服從對數正態分佈。這一假設和資產的價格變化在短期(如1天內)服從正態分佈的假設是一致的。假如大多數市場參與者接受這一假設,而你剛剛做了表10-1中的分析,從而已獲知對數正態分佈並不是一個好的關於匯率的假設,那麼你應該做什麼才能從這些結論中來盈利呢?
答案是你應該買入不同幣種的深度虛值(deep-out-of-the-money)看漲及看跌期權,接下來就是等待。這些期權相對來講比較便宜並且成為實值期權的概率要比對數正態分佈模型預測的高一些,你的期權的平均收益要比期權費用高得多。
20世紀80年代中期,有一些交易員認識到匯率分佈中的“肥尾性態”,而其他交易員仍然認為布萊克-斯科爾斯-默頓模型中的對數正態分佈合理。對匯率分佈有正確認識的交易員採用了我們描述的策略並且獲得了巨大的盈利。到了80年代後期,幾乎所有人都認識到虛值期權所對應的隱含波動率應該更高,這時套利機會消失了。
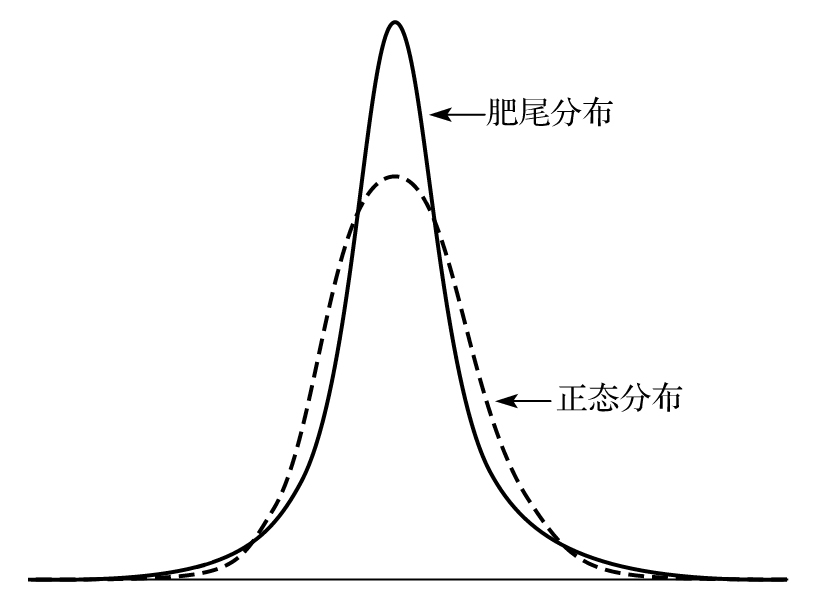
圖10-2 正態分佈與某肥尾分佈的比較
注:這裡的兩個分佈具有同樣的期望值及標準方差。
圖10-2比較了一個典型的肥尾分佈(例如匯率分佈)與一個具有同樣期望值及標準差的正態分佈。[1]肥尾分佈比正態分佈的峰值要高。在圖中我們可以看到這兩種分佈有3處不同,分別是中間部分、尾部以及介於中間及尾部的過渡部分。當從正態分佈轉移到肥尾分佈時,概率密度圖形的腰部向中央及兩尾部移動。我們在考慮市場變量的百分比變化時,肥尾分佈所對應的極大及極小變化事件的數量要比在正態分佈中相應的數量多,而相應過渡部分事件數量會少。
[1] 峰度(kurtosis)度量分佈尾部的大小。肥尾(leptokurtic)分佈比正態分佈的尾部要肥大,輕尾(platykurtic)分佈比正態分佈的尾部要瘦小,同尾(mesokurtic)分佈同正態分佈的尾部大小相等。