e1 John Hull 風險管理與金融機構 v5
9.3 利率久期
久期(duration)這一概念已經被廣泛地用來度量交易組合對於利率曲線的風險敞口。假設債券收益率為y,債券價格為B,債券的久期D的定義為

或等價於
ΔB=-DBΔy
其中Δy為債券收益率的一個小的變化,ΔB為相應債券價格的變化。因此債券久期用於衡量債券價格對收益率的敏感度。利用微積分中的符號,我們有

假定一個債券在t1,t2,…,tn時刻給債券持有者提供的現金流為c1,c2,…,cn(現金流包括券息和本金),債券收益率y是使得債券理論價格等於市場價格的貼現率。如果我們用vi來表示現金流ci以y為貼現率從時間ti貼現到當前的值,則債券的價格可表示為
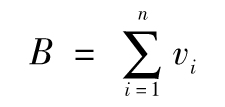
因此,債券久期D也可以定義為

式(9-3)括號中的項為ti時刻的債券支付的現金流的貼現值與債券價格的比率。債券價格等於將來所有支付的本息貼現值的總和。因此式(9-3)中久期的定義方式是付款時間ti的加權平均,而對應於ti時刻的權重等於ti時刻的現金流貼現值與債券總貼現值的比率(這裡的所有權重相加等於1),這一關係式給出了債券久期這一術語的出處。久期是指投資者收到現金流所要等待的時間。一個n年期零息債券的久期為n年,而一個n年帶息(coupon-bearing)債券的久期小於n年,這是因為國債持有者在第n年之前就已經收到部分現金付款。
如果式(9-1)中的債券收益率y以連續複利形式表示,則式(9-1)和式(9-3)是等價的(見作業題9.15)。
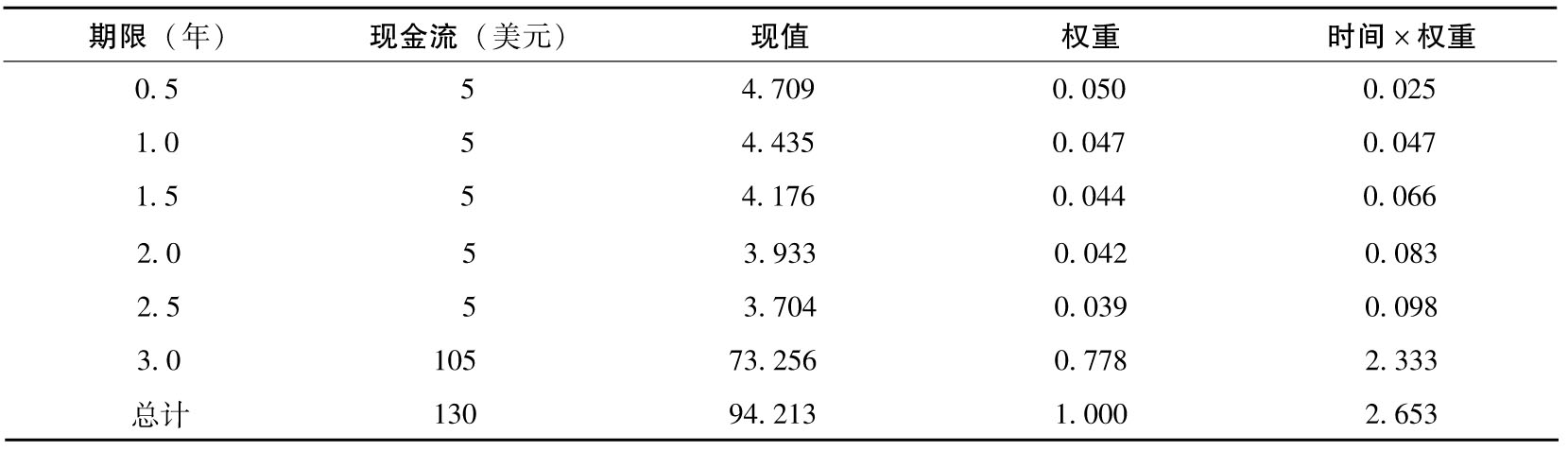
考慮某個面值為100美元、券息為10%的3年期債券。該債券連續複利的年收益率為12%,即y=0.12,每6個月付息一次,息值為5美元。表9-3顯示了有關債券久期計算的步驟,在計算中收益率代替貼現率,計算出的現值被呈現在表中的第3列(例如第一次付息的現值為5e-0.12×0.5=4.709),第3列的數字之和等於債券價格94.213,由第3列中的數字除以94.213,我們可以得到久期的權重,第5列的數字之和等於久期,即2.653年。
表9-3 久期的計算
利率的微小變化通常用基點(basis point)來描述,1個基點對應於0.01%。以下例子驗證了當久期定義為式(9-3),且收益率以連續複利形式表示時,式(9-1)是正確的。
【例9-1】 由表9-3描述的債券價格為94.213,久期為2.653,根據式(9-1)
ΔB=-94.213×2.653Δy
即
ΔB=-249.95Δy
當收益率增加了10個基點(=0.1%),即Δy=+0.001時,久期公式預計ΔB為
ΔB=-249.95×0.001=-0.250
久期公式預計債券價格會下降到94.213-0.25=93.963,為了檢驗這個預測的準確性,我們計算當收益率增加10個基點到12.1%時的債券價格,其數量為
5e-0.121×0.5+5e-0.121×1.0+5e-0.121×1.5+5e-0.121×2.0+5e-0.121×2.5+105e-0.121×3.0=93.963
這一數值同我們用久期公式預計的變化相同(精確到小數點後第3位)。
9.3.1 修正久期
式(9-3)定義的久期是由麥考利(Macaulay)在1938年首先提出的,因而這一久期被稱為麥考利久期(Macaulay’s duration),在收益率y為連續複利的前提之下,式(9-3)的定義與式(9-1)等價。由式(9-1)定義的久期,在其他複利的假設前提下,為了保證等價關係,我們必須對麥考利進行一個小的調整。如果y為一年複利一次的利率,則我們需要對式(9-3)中的久期D除以1+y;在更為一般的情況下,如果y為一年複利m次的利率,則式(9-3)中的久期D需要除以1+y/m(見作業題9.15)。對式(9-3)進行這一調整以後,所定義的久期被稱為修正久期(modified duration)。
【例9-2】 由表9-3描述的債券價格為94.213,久期為2.653。每年複利2次的收益率為12.3673%(見附錄A),修正久期為
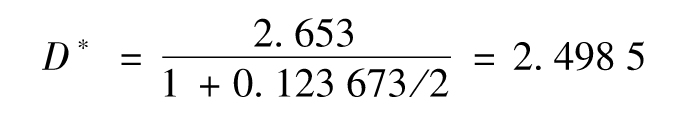
由式(9-1),我們得出
ΔB=-94.213×2.498 5Δy
或
ΔB=-235.39Δy
當收益率(一年複利2次)增加10個基點(0.1%),即Δy=+0.001時,久期關係式預計債券價格變化ΔB為-235.39×0.001=-0.235,因此債券價格下降到94.213-0.235=93.978。當收益率(一年複利2次)增加10個基點,即對應收益率y=12.4673%(或連續複利收益率增加10個基點,即對應收益率為12.0941%)時,通過一個幾乎與前面的例子相同的計算,我們得出的債券價格為93.978。這一例子說明:當債券收益率變化較小時,修正久期計算公式非常精確。
9.3.2 絕對額久期
絕對額久期(dollar duration)等於修正久期與債券價格的乘積,如果D$代表絕對額久期,由式(9-1)得出
ΔB=-D$Δy
採用微積分的記號
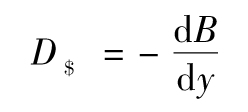
久期為債券相對價格變化(即債券價格變化與債券價格的比率)與收益率變化建立了聯繫,而絕對額久期將債券價格變化與收益率變化建立了聯繫,絕對額久期類似於我們在第8章中討論的delta測度。