e5 Mishkin 貨幣金融學 v2
4.2 利率和回報率的區別
許多人認為債券的利率包含持有債券獲得回報的全部內容。如果投資者歐文認為,在他持有利率為10%的長期債券而市場利率上升至20%的時候,他的經濟福利將會提高的話,他將會恍然大悟:正如我們隨後將會發現的那樣,如果歐文此時出售債券,他將血本無歸。回報(return),或者在術語上更精確的是回報率(rate of return),是精確衡量人們在特定時期持有某種債券或者任何其他種類證券獲得回報的指標。在本書中,我們將會始終使用回報率這一概念:如果你理解了回報率的概念,就會更加容易地掌握本書隨後表述的內容。
對於任何證券而言,回報率是指持有者獲得的利息收入再加上證券價格的變化,它表示為證券購入價格的一定比率。為了使回報率的定義更加清晰,讓我們考察一個例子:面值1000美元的息票債券,其息票利息為10%,而購入價格為1000美元,在持有1年後,以1200美元的價格出售,其收益率應該是多少?債券持有人息票利息收入為100美元,證券價格變化為1200美元-1000美元=200美元,將這兩項相加並且表示為購入價格1000美元的百分數,我們將會得到這種證券持有期為1年的回報率:

對於這個計算結果——回報率30%,你也許會感到十分驚訝;而根據表4-1所示,其初始到期收益率僅為10%。這證明了債券的回報率和到期收益率不一定相等。現在我們發現,儘管對於許多證券而言,回報率和利率密切相關,然而利率和回報率之間的區別是十分重要的。
從t到t+1時刻之間,持有債券獲得回報率的更一般形式是

式中,R為從t到t+1時刻之間持有債券所獲得的回報率;Pt為t時刻的債券價格;Pt+1為t+1時刻的債券價格;C為利息收益。
把式(4-7)分為兩個部分,回報率公式可以更簡便地寫為:

第一部分是當期收益率ic(利息收益除以購入價格):

第二部分是資本利得率(rate of capital gain),即債券現期價格相對於其初始購入價格的變化:

式中,g是資本利得率。
式(4-7)可以重新寫為:
R=ic+g (4-8)
式(4-8)表明,債券回報率是當期收益率ic和資本利得率g之和。這個重寫的公式使我們認識到:即使當期收益率是精確衡量債券到期收益率的指標,但是回報率和利率之間會存在很大的差別,特別是在債券價格出現大幅波動,導致資本利得出現劇烈變化的時候,兩者之間的差別更為顯著。
為了對此進行深入討論,讓我們考察在利率上升的條件下不同期限債券的回報率變化。表4-2提供了當利率從10%上升至20%的條件下,按照面值購入的、息票利率為10%的不同期限債券1年期回報率結算結果。從該表中,我們可以得出適於所有債券的幾個重要結論。
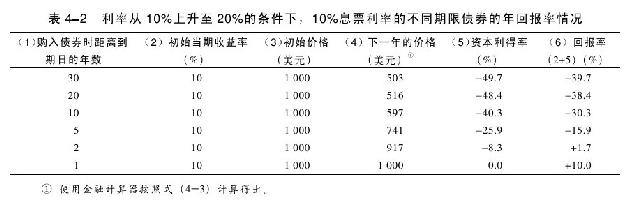
·只有在距離到期日的期限與債券持有時間相等時,債券的回報率將會等於其初始到期收益率(表4-2中的最後一種債券)。
·如果距離到期日的期限長於持有債券的期限,那麼利率的上升必將伴隨著債券價格的下跌,從而導致債券出現資本損失(資本利得為負)。
·距離債券到期日的期限越長,債券價格和利率的波動幅度也會越大。
·距離債券到期日的期限越長,當利率上升的時候,債券的回報率就會越低。
·儘管債券具有很高的初始利率,但是在利率上升的條件下,債券的回報率也有可能為負。
利率上升可能意味著購買債券是一項糟糕的投資活動,這一點也許經常讓學生們在開始時感到困惑。理解這一問題的關鍵在於,要意識到利率的上升就意味著債券價格的下跌。因此,利率的上升也就意味著會發生資本損失。如果資本損失足夠大,那麼這項債券投資就是一項失敗的投資活動。舉例來說,在表4-2中我們發現,在利率從10%上升到20%的條件下,距離到期日還有30年債券的資本損失為49.7%,遠遠超過10%的當期收益率,從而導致-39.7%的負回報率(損失)。如果歐文不賣出這些債券,他的資本損失通常稱為“賬面損失”。無論如何,它仍然是一種損失,因為如果原來沒有購買這種債券而是將資金存在銀行裡,那麼他現在就可以按照較低的價格購入比以前更多的債券。
4.2.1 期限與債券回報率:利率風險
債券期限越長,其價格變動幅度受到利率的影響會越大。這個發現有助於我們理解債券市場行為中一個重要的事實:長期債券的價格和回報率波動幅度比短期債券要大。對於距離到期日還有20年以上的債券而言,其價格和回報率在1年內出現20%±的變化是十分正常的。
現在我們發現,利率變化能夠加大長期債券的投資風險。實際上,由於利率變化導致的資產收益率風險變動問題十分重要,所以使用一個專門的術語——利率風險(interest-rate risk)[1]。正如我們在隨後章節中發現的那樣(也可參見參考資料專欄),對於金融機構的管理者和投資者而言,利率風險的管理活動是一項主要的工作。
參考資料 幫助投資者選擇適當的利率風險
由於許多投資者希望瞭解其面臨的利率風險水平,所以一些共同基金試圖向投資者提供關於利率風險危害程度的知識,並且提供與投資者風險偏好相匹配的多種投資選擇。
舉例來說,先鋒集團向投資者提供了8種不同的高評級債券型共同基金。在其計劃書中,先鋒集團按照債券的平均期限對基金進行分類,並且通過計算1%的利率波動造成的債券價值的變化來說明利率風險程度。其中,先鋒集團將三種債券型基金歸為具有最低利率風險的種類,其所投資債券的平均期限為1~3年;將另外三種債券型基金歸為具有中等利率風險的種類,其所投資債券的平均期限為5~10年;將兩種債券型基金歸為具有最高利率風險的種類,其所投資債券的平均期限為15~30年。
通過提供這些信息,先鋒集團希望能夠獲得在債券型基金市場中的更大份額。毫無意外的是,先鋒集團因此成為最成功的共同基金公司之一。
雖然持有長期債務工具會面臨相當大的利率風險,但是持有短期債券就不會這樣。實際上,那些距離到期日期限和持有期限相同的債券是沒有這種利率風險的[2]。從表4-2最後一種息票債券的例子中,我們可以看到這一點。由於在購買債券時,其回報率就已經確定並且等於其到期收益率,所以這種息票債券的回報率是確定的。要理解那些距離到期日期限和持有期限相同的債券不存在利率風險,其關鍵是要認識到(在這個事例中)債券持有期期末的價格已經被確定為其面值。因此,該債券持有期期末的價格就不會受到利率變化的影響,其回報率就等於在購入債券時已經確定的到期收益率[3]。
[1]我們使用久期(duration)這一概念來衡量利率風險。
[2]只有對在持有期結束之前沒有現金利息支付的貼現發行債券和零息債券而言,距離到期日期限和持有期限相同不會產生利率風險這一論斷才是正確的。對於那些在持有期限內能夠獲得現金利息支付的息票債券而言,獲得的現金利息支付款項可以用於再投資活動。由於不能確定再投資活動的利率,所以對於那些距離到期日期限和持有期限相同的債券而言,其回報率也包含著一定的不確定性。然而,由於使用持有息票債券獲得的息票利息進行再投資的風險相當小,所以那些距離到期日期限和持有期限相同的息票債券面臨的利率風險基本上是可以忽略不計的。
[3]在課本正文中,我們假定債券的持有期限比較短,並且都等於短期債券距離到期日的期限,因此不會出現利率風險。然而,如果投資者持有債券的期限長於債券距離到期日的期限,那麼投資者就會面臨再投資風險的利率風險。由於投資者使用其憑藉短期債券投資獲得的收入進行再投資,而再投資活動所包含的未來利率是不確定的,所以就產生了這種再投資風險。
為了更好地理解再投資風險,我們假設投資者歐文進行債券投資活動的期限為2年,他首先購買的是面值為1000美元的1年期債券,然後在第1年年末再投資購買另一種債券。如果初始利率為10%,那麼在第1年年末,歐文就獲得了1100美元。假如此時利率上升為20%,即如表4-2所示,歐文會發現,如果再次購買1100美元的這種1年期債券,那麼在第2年年末他可以獲得1100美元×(1+0.20)=1320美元。因此,歐文在這兩年中的回報率為(1320美元-1000美元)/1000美元=0.32=32%,即年回報率為14.9%。在這種情況下,歐文購買1年期債券所獲得的回報就要高於他最初購買10%利率的2年期債券所獲得的回報。因此,在歐文持有債券的期限超過其購買債券距離到期日期限的條件下,他能夠從利率上漲中獲取回報。相反,如果利率下降至5%,那麼在第2年年末歐文只能夠獲得1100美元×(1+0.05)=1155美元,這樣歐文在這兩年中的回報率為(1155美元-1000美元)/1000美元=0.155=15.5%,即年回報率僅為7.2%。因此,在持有債券的期限超過債券距離到期日期限的條件下,歐文將會因為利率下降而蒙受損失。
我們發現,當持有債券的期限超過債券距離到期日的期限時,由於再投資的未來利率存在不確定性,所以這種投資的回報率是不確定的。簡言之,就是存在再投資風險。我們還可以發現,當持有債券的期限超過債券距離到期日的期限時,投資者可以從利率的上升中獲利,也可以由於利率下跌而蒙受損失。