e4 Robert Jacobs 運營管理 v15

應用舉例

20-2

例1

某產品的單位售價為100美元，單位成本保持70美元不變。每一單位未售出的產品的殘值為20美元。在週期內的期望需求為35～40單位；至少能售出35單位，但超過40單位是一定不能售出的。需求概率及相關的累計概率分佈（P）如下表所示。

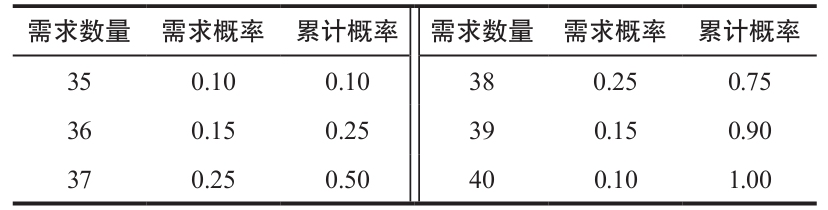
需要訂購多少單位？

解答

低估需求的成本也就是利潤的損失，即Cu =100-70=30（美元/單位）。高估需求的成本也就是當產品不得不以殘值出售時的損失，即Co =70-20=50（美元）。

未售出的最佳概率為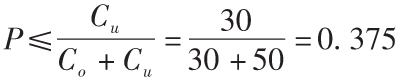

根據上面的分佈數據，對應的是第37單位。

以下是該問題完整的邊際分析。注意，最小成本出現在訂購37單位時。

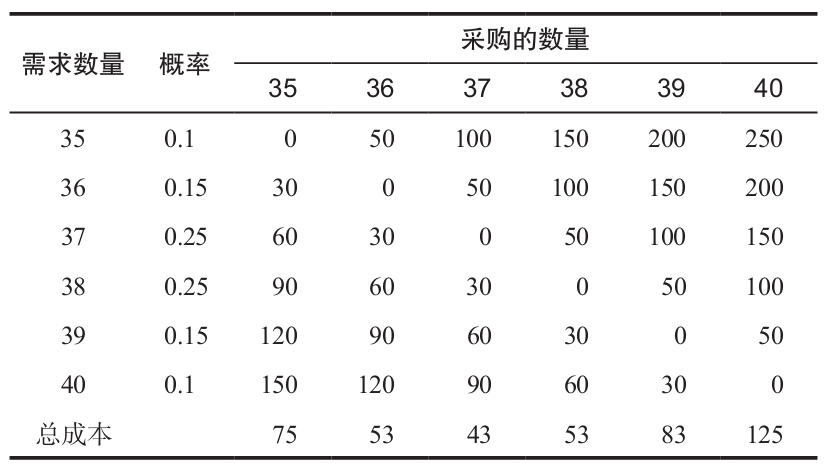
例2

從賣方採購產品的單位成本為20美元，下一年的預測需求為1 000單位。如果每次發出訂單的成本為5美元，單位產品年庫存成本為4美元。回答下列問題：

a.每次應該訂購多少單位？

b.一年的總訂購成本為多少？

c.一年的總持有成本為多少？

解答

a.每次的訂貨數量為：

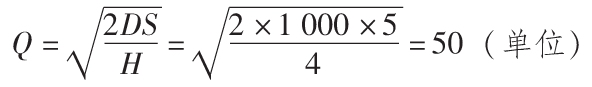
b.一年的總訂購成本為：

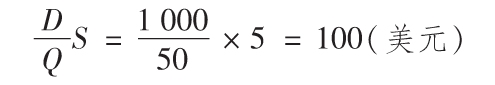
c.一年的總持有成本為：

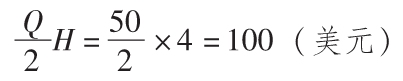
例3

某一產品的日需求量為120單位，標準差為30單位。檢查週期為14天，提前期為7天。檢查時，庫存量為130單位。如果可接受的缺貨概率僅為1%，應該訂購多少單位？

解答

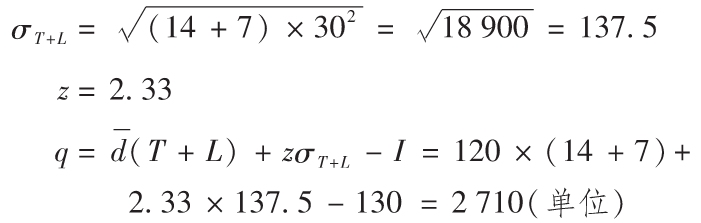
例4

一家企業現有200單位某產品庫存，銷售人員每兩週來訪一次，該企業就在此時訂貨。該產品的平均日需求為20單位，標準差為5單位。提前期為7天。管理層要求95%的不缺貨概率。

銷售人員將於今天下午來訪，此時剩餘的庫存為180單位（假設今天售出了20單位）。需要訂購多少單位？

解答

已知I=180，T=14，L=7，d=20

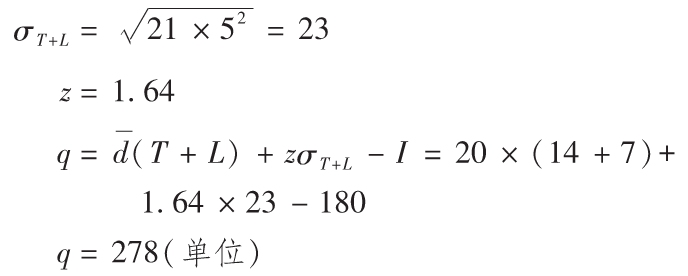
例5

金屬板加工公司（SMI）是金屬板供應的龍頭老大，臺式計算機和電子設備的製造商是其主要的客戶。SMI訂購了一批種類不多但數量較大的原材料。採購部門正要建立一條訂購政策以最小化總成本同時滿足公司需求。其中一個最大量的訂購是向鋼鐵處理商發出的裁剪鋼鐵。根據歷史數據的預測表明SMI需要採購200 000個薄板。鋼鐵製造商擁有最低1 000個薄板的採購量，並且根據訂購量有一定的浮動價格，如下所示。

採購部門估計每次採購需要花費300美元，SMI的庫存成本為庫存價值的15%。

根據這些信息，利用價格分界模型來確定最佳訂貨量。

解答

第一步是將題目中的信息匹配到模型中的合適位置。

D=200 000單位（每年需求）

S=單個訂單的分配和處置成本300美元

I=單位成本的15%

C=單位成本，根據上表中的訂購量有不同的價格

下一步是以最低單位成本計算出在每個價格初始點的經濟的訂購規模，當得到一個合適的訂購量Q時即停止。

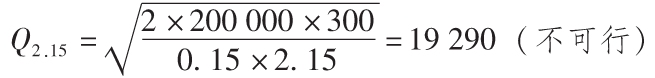
在2.15美元的價格上計算出的EOQ不可行，因此該價格點上的最佳訂購量是30 000個單位。

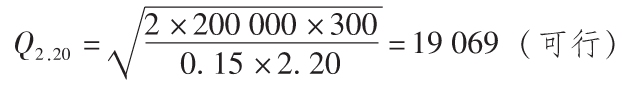
在2.20美元的價格上計算出的EOQ是可行的，因此該價格點上最佳訂貨量是19 069個單位。我們找到了一個可行的EOQ，不需要再考慮其他更高的價格點。需要考慮的兩個訂購策略如下：以2.15美元的單價訂購30 000個單位和以2.20美元的單價訂購19 069個單位。問題是以2.15美元的價格訂購能否抵銷更高訂購量產生的更高庫存成本。為了回答這個問題，要計算每種方案的總成本。

最低的總成本是訂購量為30 000、價格為2.15美元時的成本，因此這是最佳的訂購策略。你是否奇怪5美分的差別會導致總成本如此的不同？當採購大批量的貨物時，每個細微的價格變動都會對總成本有很大的影響。