e4 Robert Jacobs 運營管理 v15
4.2 網絡計劃模型
最著名的兩種網絡計劃模型都產生於19世紀50年代。關鍵路徑法 （critical path method，CPM）是杜邦公司旗下的化工廠在制訂停機期間的維護計劃時發明的。由於這個行業經常要進行維護項目，所以對這些維護活動有較為準確的時間預計。關鍵路徑法的假設前提是項目中各項活動所需的時間都能準確預計，且這些時間都不發生變化。計劃評審技術法 （program evaluation and review technique，PERT）是從美國海軍制訂北極星導彈研製計劃發展起來的。這是一個涉及了3 000個承包商的特大型項目，由於其中大部分的工作以前都沒有做過，所以計劃評審技術法就被用來解決不確定時間的估計問題。隨著時間的推移，關鍵路徑法和計劃評審技術法之間的差異逐漸消失，在這裡我們把它們都稱為關鍵路徑法（CPM）。
從某種意義上講，CPM的發展應歸功於其原型——甘特圖。對小項目，用甘特圖可以直觀地將各種活動和時間聯繫起來，但對於由超過25個活動組成的項目，其可視性就變得極差，而且操作起來也十分困難。
在一個項目中，關鍵路徑 （critical path）是一連串的活動，表示在項目完成過程中花費時間最長的一條路線。如果關鍵路徑上的某一項活動延期，整個項目就將延期。很多時候，一個項目可以同時具有多條關鍵路徑。確定項目中每一個活動的時間是CPM技術的主要目標。這個技術可以計算出每一個活動的開始和結束時間，以及該活動是否為關鍵路徑的一部分。
4.2.1 關鍵路徑法
下面是一個項目的計劃過程，在這個項目中，我們假設活動的時間都是已知的，因此給出了活動時間的唯一估計值。我們為一個簡單的項目安排時間，來說明這個基本的方法。
現在假設你們小組需要做出決定——是否投資於某家公司。投資顧問建議你通過下面的4步來進行分析：
新西蘭TE APITI風電場項目建造了南半球最大的風電場，從委託到完成只用了一年的時間，該項目在預期時間內準時完成。在進行有效的項目管理和使用合適的技術工具的基礎上，Meridian能源公司提供了一個可行的能源再生方案，這一項目也成為之後風電場項目的標杆。
A.選擇一家公司。
B.獲得這家公司的年報並做出比率分析。
C.收集技術股票價格數據並建立圖表。
D.獨立審核這些數據並做出決定，是否應該買這家公司的股票。
你們小組的4個成員決定按照投資顧問的建議將這個項目分成4個活動。你決定要讓所有的成員都參與選擇公司，並且這項任務要在一週之內完成。你們將在週末碰頭，決定你們小組想要投資的公司。在這次會議上，你們將進行分組：兩個人負責年報和比率分析，其他兩個人負責技術數據和建立圖表。你們小組希望花費兩週時間取得年報並做出比率分析，花費一週時間來收集股票價格數據並做出圖表。你同意讓這兩個小組獨立開展工作。最後你們將在一起決定是否購買該公司的股票。但在此之前，每一個小組成員都要花費一週的時間對所有的數據進行審核。
這是一個簡單的項目，但是它可以說明這種方法。下面就是相應的方法步驟。
（1）確定項目中每一個需要完成的活動，並估計完成每一個活動所需要的時間。 這一點很簡單，你可以從投資顧問那裡得到信息。所有活動如下：A（1），B（2），C（1），D（1）。括號中的數字就是活動所需要的時間。
（2）確定活動次序，建立起能夠反映活動次序的網絡。 首先要確定每個活動的緊前活動，緊前活動 （immediate predecessors）指的是在進行這個活動之前必須要完成的活動。活動A需要在活動B和C開始之前完成。活動B和C需要在進行活動D之前完成。這些關係如下表所示。
下面是一個描述前後次序關係的網絡圖。
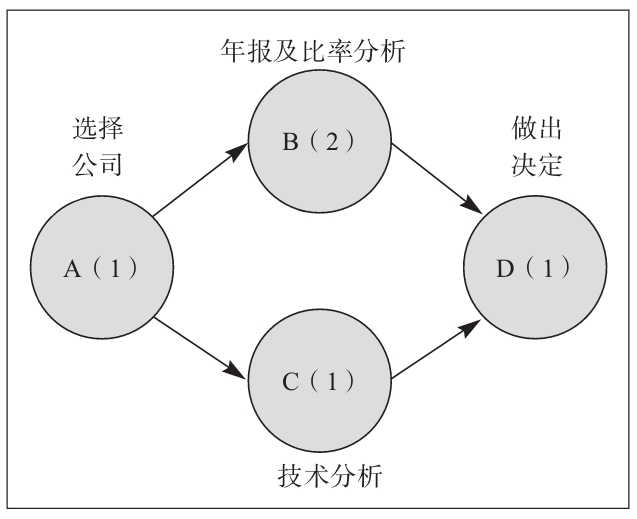
（3）確定關鍵路徑。 分析項目中從起點到終點的每一個路徑。對於這個簡單的項目來說，有兩條路徑：A-B-D和A-C-D。關鍵路徑就是總時間最長的一條路徑。A-B-D路徑的時間為4周，而A-C-D路徑的時間為3周。因此路徑A-B-D就是關鍵路徑，如果這條關鍵路徑上的任何活動延期，整個項目都將延期。
（4）確定最早開始／結束時間以及最晚開始／結束時間。 為了安排整個項目，就要找出每一個活動的開始時間和結束時間。但是對一些活動來說，在活動開始和結束的時候會存在一個時間上的餘量，這個餘量就叫作活動的鬆弛時間 （slack time）。對於項目中的每一個活動，我們要確定4個時間：最早開始時間、最早結束時間、最晚開始時間、最晚結束時間。最早開始時間和最早結束時間就是這個活動最早能夠開始和結束的時間。同樣，最晚開始時間和最晚結束時間就是在不影響整個項目工期的情況下活動最晚開始和結束的時間。最晚開始時間和最早開始時間之間的差就是鬆弛時間。為了能夠直觀地表示出來，我們在表示活動的符號旁邊分別添加了這些數據，如下圖所示。
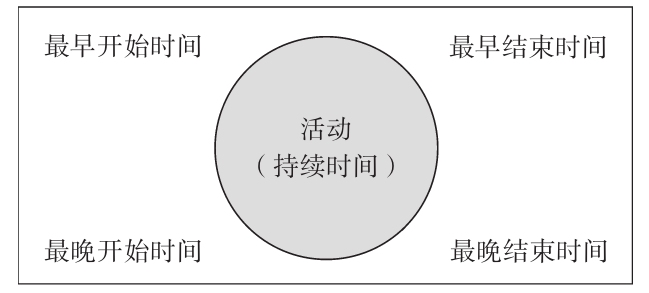
我們可以從網絡圖的開始活動到結束活動分別計算出每一個活動的最早開始與最早結束時間。設定我們的開始時間為0。活動A的最早開始時間為0，最早結束時間為1。活動Ｂ的最早開始時間是活動A的最早結束時間，也就是1。同樣，活動C的最早開始時間為1。活動B的最早結束時間為3，活動C的最早結束時間為2。現在考慮活動D，只有活動B、C完成才能進行活動D，由於活動B的最早結束時間是3，所以活動D的最早開始時間為3，最早結束時間為4。至此，我們的圖如下所示。
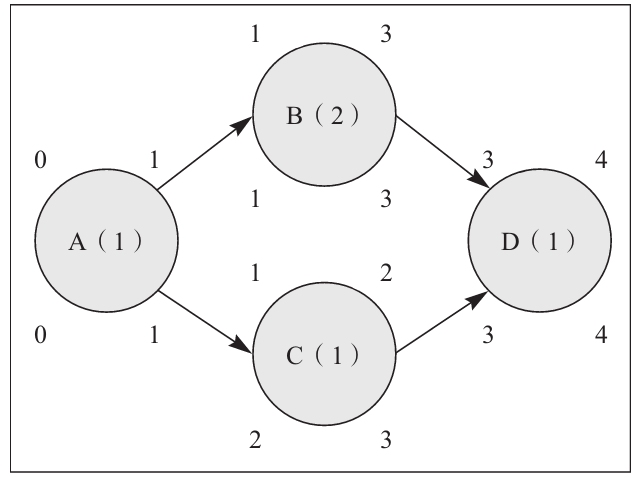
計算最晚結束和最晚開始時間，需要從網絡圖的結束活動開始，計算到網絡圖的開始活動為止。考慮活動D，它的最晚結束時間是4，如果我們不想推遲項目的完成時間，活動D的最晚結束時間應為4。由於有1個時間單位的工期，活動D的最晚開始時間就是3。現在來看活動C，活動C應該在活動D開始的時刻3完成，所以活動C的最晚結束時間為3，因此最晚開始時間就是2。注意活動C的最早時間和最晚時間的差，我們就會發現這裡有1周的鬆弛時間。活動Ｂ應該在時刻3完成，因此活動Ｂ的最晚結束時間為3，而最晚開始時間為1。在活動B上並沒有鬆弛時間。最後，活動A必須在活動B和C之前完成。由於活動B的開始時間早於C，所以活動A在B開始之前就需要完成，因此活動A的最晚結束時間為1，最晚開始時間為0。我們注意到活動A、B、D並沒有鬆弛時間。最終的網絡圖如下所示（希望你的小組在股票投資中能夠成功）。
例4-1 關鍵路徑法
許多試圖進入筆記本電腦市場的公司都以失敗告終。現假設你的公司仍相信該市場有很大的需求，因為現有產品的設計不符合用戶的要求。它們或者太重，或者太大，或者太小，以至於不能安裝標準尺寸的鍵盤。你設想中的計算機可以小到能放在衣服的口袋裡，其理想的尺寸是不超過5英寸×9.5英寸×1英寸，並且配有一個摺疊鍵盤。這種計算機的重量不能超過15盎司 [1] ，並配有一個液晶顯示屏、一個微型軟驅以及一個以太網卡的插槽。它主要是為經常出差的業務人員所設計的，但它也擁有包括學生在內的更廣闊的市場。它的價格定位應該在175～200美元。
該項目是設計、開發和製造微型計算機的樣機。對於瞬息萬變的計算機市場，該項目的關鍵是要在不到1年的時間內將新產品投放市場。因此，該項目小組必須在大約8個月（35周）的時間裡生產出樣機。
解答
項目小組的第一個任務是繪製項目網絡圖，然後估計在35周內完成計算機樣機的可能性，現在我們依照編制網絡圖的步驟來做。
（1）確定活動。 項目小組確定下列活動是該項目的主要活動：設計樣機、試製樣機、樣機檢測、編寫試製報告（在報告中對樣機試製方法進行總結）、對自動生產線設備的調查與評估、完成生產線設備的調查報告、完成總結報告（包括設計、設備和方法等所有方面）。
（2）活動排序及網絡圖的構建。 在與項目小組成員討論後，項目經理建立了活動的優先順序表以及相應的網絡圖，如圖4-4所示。建立網絡圖的時候，要注意確保活動順序的正確性和活動之間的邏輯關係，例如，如果設定活動A後面是活動B，活動B後面是活動C，活動C後面是活動A，顯然是不符合邏輯的。
（3）確定關鍵路徑。 關鍵路徑是網絡中完工時間最長的一條活動序列，即這個序列中不含有鬆弛時間。這個網絡有4條不同的路線，分別為：A-C-F-G、A-C-E-G、A-B-D-F-G和A-B-D-E-G。這些路徑的長度分別為38周、35周、38周和35周。由此我們注意到，該項目有兩條關鍵路徑，表明這個項目可能較難管理。通過編制最早開始和最晚開始計劃表，我們進一步發現這個項目確實很難按時完成。
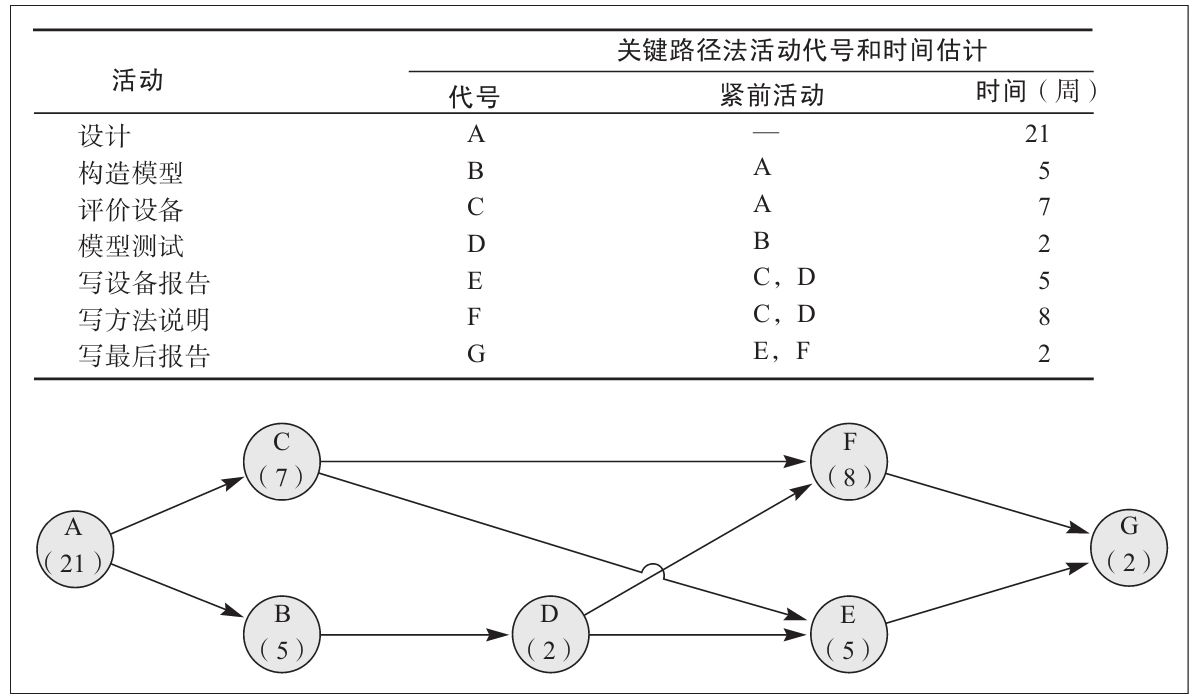
圖4-4 計算機設計項目的關鍵路徑網絡圖
最早開始計劃表與最晚開始計劃表
最早開始計劃表 （early start schedule）是按照最早開始時間的所有活動的列表。非關鍵路徑上活動的完成時間和下一活動的開始時間之間具有鬆弛時間。最早開始計劃表是為了儘早完成所有活動，從而儘早完成項目。
最晚開始計劃表 （late start schedule）是在不影響項目工期的情況下，每個活動最晚開始的時間列表。使用最晚開始計劃表的目的是通過推遲購買原材料、使用人工及降低其他成本來實現成本節約。這些計算如圖4-5所示，從圖中我們可以看到，唯一具有鬆弛時間的活動是E。因此這肯定是一個很難按時完成的項目。
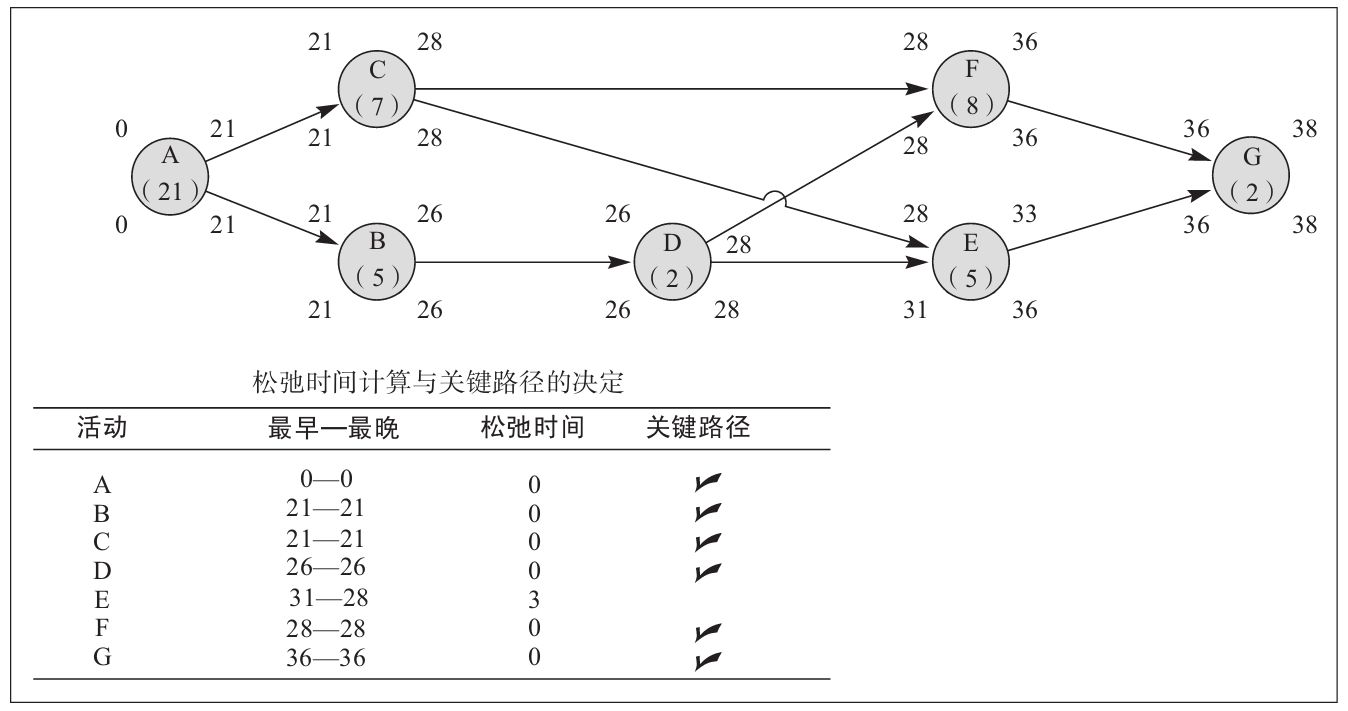
圖4-5 考慮鬆弛時間計算的計算機設計項目關鍵路徑網絡圖
4.2.2 具有三點時間估計的關鍵路徑法
如果單點時間估計可靠性不高的話，最好的解決辦法是使用三點時間估計。三點時間估計不僅要估計活動時間，而且要估計整個項目在規定時間內完成的概率。其估計過程如下：活動時間的估值是最悲觀時間、最樂觀時間和最可能時間的加權平均值。項目網絡的完成時間可以用我們前面所說的步驟來估算。通過估計關鍵路徑活動的時間變動，可以估算出在特定時間內完成項目的概率（注意，概率計算是經典PERT方法的一個顯著特徵）。
例4-2 三點時間估計法
本案例描述與例4-1相同，只是需用三點時間估計法來計算例4-1中的活動時間。
解答
（1）識別項目需要完成的活動。
（2）確定活動順序，構建反映活動優先順序關係的網絡圖。
（3）對完成每一活動所需的時間做三點時間估計：
a——最樂觀時間：完成某項活動需要的最短可能時間（活動在更短的時間內完工的可能性很小，通常設定為1%）。
m——最可能時間：完成某項活動最可能需要的時間。m是最可能發生的時間，因此它通常服從第4步要討論的β分佈。
b——最悲觀時間：完成某項活動需要的最長可能時間（活動需要更長時間才能完成的可能性也很小，通常設定為1%）。
在一般情況下，這些數值要從負責完成活動的人員那裡獲得。
（4）計算每個活動的期望時間（ET）。計算公式是：
該公式基於β分佈，賦予了最可能時間（m）4倍於最樂觀時間（a）和最悲觀時間（b）的權重。β分佈的靈活性極大，它可以用於通常發生的許多形式，有確定的區間點（限定了可能的活動時間的範圍是在a和b之間），允許直接計算活動的平均值和標準差。
（5）確定關鍵路徑。根據計算得到的活動期望時間來計算關鍵路徑。
（6）計算活動時間的方差（σ2 ）。與每一個期望時間有關的方差計算公式是：
我們看到，方差是兩個極端時間估計之差的1/6的平方。當然，時間差距越大，方差就越大。
（7）在應用標準正態分佈的基礎上確定項目在給定日期之內完工的概率。三點時間估計法最有價值的特點是，它可以估計出不確定因素對項目完工時間的影響（如果你對概率類型不熟悉的話，可以參照專欄4-1“概率分析”）。估計該概率的方法步驟如下。
a.計算關鍵路徑的各項活動的方差值。
b.將該值與規定的項目到期時間和期望的項目完工時間代入Z變換公式。該公式如下：
式中 D——項目的必須完工日期；
TE ——項目的期望完工時間；
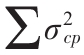——關鍵路徑上所有方差的總和。
c.計算Z值，Z值是項目規定完工日期與項目期望完工時間偏離標準差的數值（正態分佈）。
d.利用Z值計算符合項目完工日期的概率（利用附錄G的正態分佈表），期望完工時間是項目開始時間加上關鍵路徑上的活動持續時間之和。
遵循上述步驟，我們得到了如表4-1所示的期望時間和方差。項目網絡的建立方法與前面的方法一致，唯一的不同是活動時間採用的是加權平均值。確定關鍵路徑時，把它們當作單一數值。單點時間估計和三點時間估計（最樂觀時間、最可能時間、最悲觀時間）的不同在於，三點時間估計要計算完工的概率。圖4-6顯示的是網絡圖和關鍵路徑。
表4-1 活動的期望時間和方差
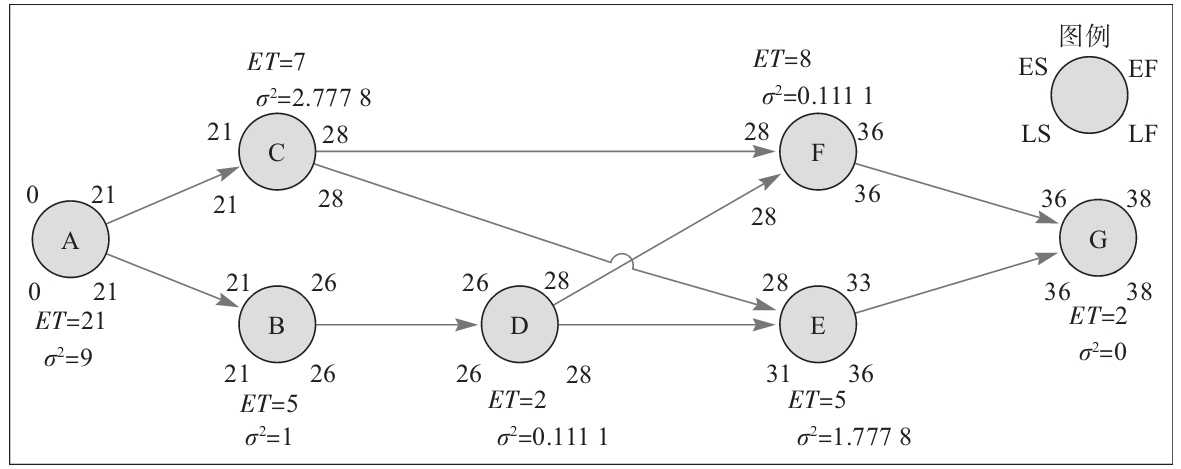
圖4-6 應用三點時間估計法的計算機設計項目
在網絡中有兩條關鍵路徑，我們必須決定哪一個方差滿足項目在目標日期完工的概率。一個保守的方法是使用總方差最大的關鍵路徑來計算完工概率，把注意力集中在那些時間波動最大的活動中。在這個基礎上，利用活動A、C、F和G的方差確定完工的概率，則可得到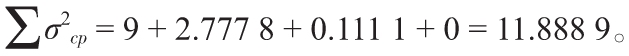
若要求在35周內完成項目的概率，則D=35，期望的完工時間是38。把這些值代入Z公式，我們得到：
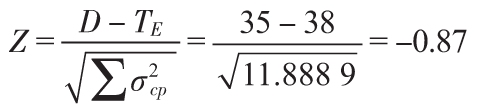
查附錄G，Z=-0.87對應的概率值是0.192 2，這意味著項目經理在35周內完成任務的可能性大約只有19%。請注意，該概率事實上是關鍵路線A-C-F-G的完工概率。因為本項目還存在另一條關鍵路徑，其他路徑也可能變得關鍵。因此本項目在35周內完成項目的概率事實上小於19%。
|專欄4-1|
概率分析
三點時間估計法可以計算出在某個特定時間內完成一個項目的可能性。這個假設的前提是每一個活動所需要的時間都是一個獨立的隨機變量。如果這些都成立，就可以使用中心極限定理來找出關鍵路徑上每一個活動的平均數和方差。中心極限定理告訴我們，隨著隨機變量的增加，這些獨立的變量將會呈正態分佈。在項目管理中，隨機變量就是完成每一個活動所需的時間（假設每個活動所用時間是相互獨立的，且服從統計分佈）。因此，完成關鍵路徑上活動的期望時間就是各活動時間的總和。
同理，由於假設活動所需時間是相互獨立的，所以關鍵路徑上活動的方差之和就是完成關鍵路徑所需要時間的方差。標準方差即為方差的平方根。
為了確定在某一特定時間內完成項目的概率，我們要找出在概率分佈圖表中何時會降低。附錄E給出了在Z取不同的數值時的標準分佈形式。Z表示了在分佈中0左邊和右邊的偏差。參照附錄E，G（z）的值就是在分佈圖形上曲線下的面積。每一個Z數值都對應著一個可能性。例如在表中的第一個數值-4.00，相對應的G（z）就等於0.000 03，它表示Z值是-4.0的概率只有0.003%。同樣，當Z等於1.50的時候，G（z）就等於0.933 19或者93.319%。Z的數值可以通過使用例4-2中的式（4-3）得到。這些概率值可以通過微軟Excel軟件中的NORMSDIST（z）功能來得到。
4.2.3 時間-費用模型和項目趕工
實際中，項目經理對項目成本的關心程度絕不亞於對工期的關心。因此，時間 -費用模型 （time-cost models）就應運而生了。這些模型作為基本關鍵路徑法的拓展，試圖為整個項目建立最小成本計劃，以控制項目執行期間的費用。
最小費用計劃（時間-費用均衡）
最小費用計劃也叫趕工（crashing），其基本假設是活動的完成時間與項目費用之間存在一定的關係。趕工是指壓縮項目工期。一方面，要有資金來保證各項活動的進行；另一方面，需要資金來維持項目實施。與活動有關的費用稱為活動的直接費用，加總得到整個項目的直接費用。這些費用可能是與人工有關的費用，如加班費、僱用更多工人的支出以及從其他崗位調用工人的費用；另外一些費用可能與資源消耗有關，例如購買或租賃附加設備、高效率設備以及借用輔助設施的支出。
與維持項目正常進行有關的費用稱為項目的間接費用，包括日常管理費用、設施維護費用、資源的機會成本以及在有合同約束下的罰款和獎金支出。因為活動的直接費用和項目的間接費用都隨時間變化，所以制訂計劃的關鍵問題就是尋找具有最小總費用的項目工期，換句話說，就是找到時間-費用的最優平衡點。
例4-3 時間-費用均衡的過程
項目趕工由以下5個步驟組成。下面我們通過圖4-7中4個簡單的活動網絡圖來進行說明。假設在項目的前8天，間接費用保持每天10美元不變。如果項目時間超過8天，則間接費用按照每天5美元的速度增加。
（1）繪製關鍵路徑網絡圖 。 針對每一個活動，需要給出以下信息：
a.常規費用（NC）：活動的最低期望費用（圖4-7中每個節點下面列出的費用中的較小者）。
b.常規時間（NT）：與每一常規費用相對應的時間。
c.趕工時間（CT）：活動最短可能完成時間。
d.趕工費用（CC）：與每一趕工時間相對應的費用。
（2）確定每項活動的趕工費用率（單位為天）。 活動的時間和費用之間的關係可用圖來表示：標出點（CC，CT）的座標，將該點與座標點（NC，NT）連接起來，連接曲線可為凹曲線、凸曲線、直線或其他形式的曲線。圖形的形式主要取決於活動的實際費用結構，如圖4-7所示。對於活動A，我們假設時間和費用之間是線性關係。這種假設在實際工作中經常使用，它有助於計算趕工費用率，此時趕工費用率的值就等於該直線的斜率，可用公式：斜率=（CC-NC）/（NT-CT）直接計算出來（當不能使用線性假定時，趕工費用必須用圖形確定，因為活動工期在每一天都可能在縮短）。
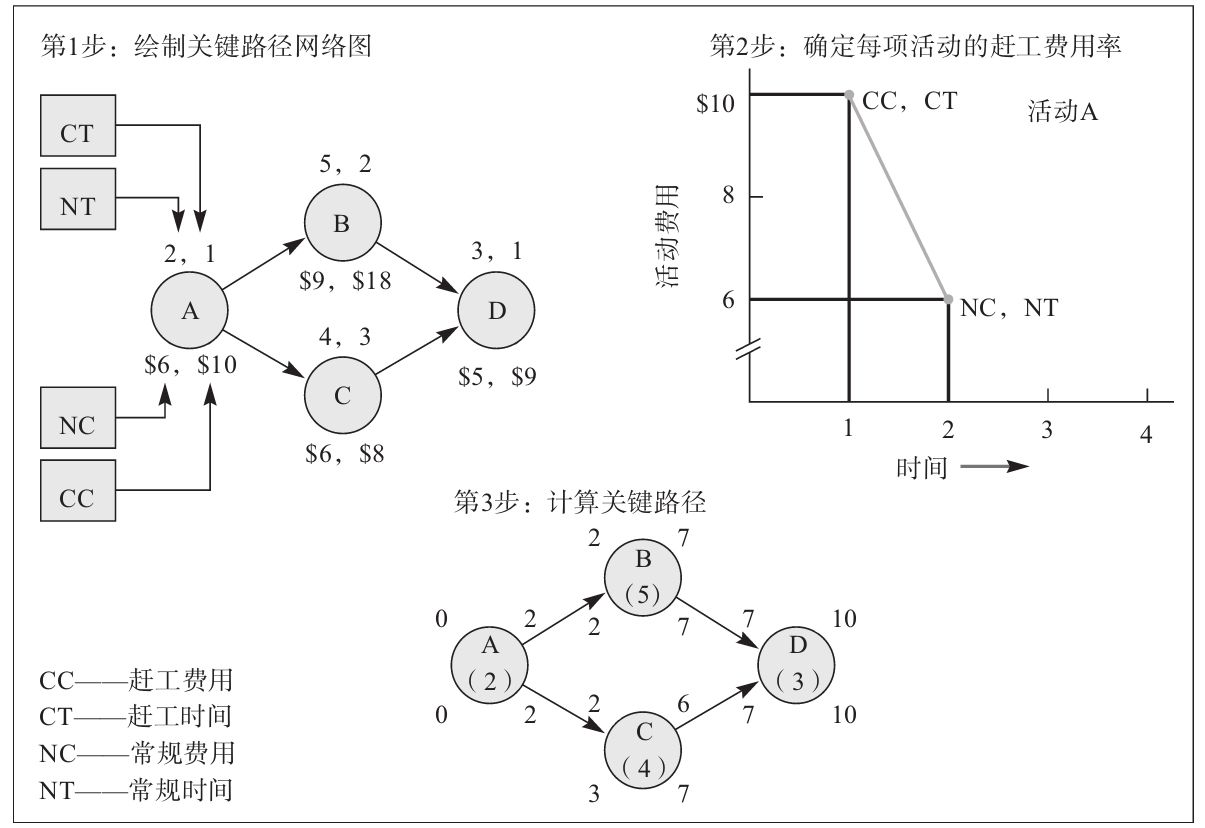
圖4-7 時間-費用均衡模型的例子
活動的趕工費用率的計算過程如表4-2所示。
表4-2 對每個活動進行趕工所需的費用計算（天） （金額單位：美元）
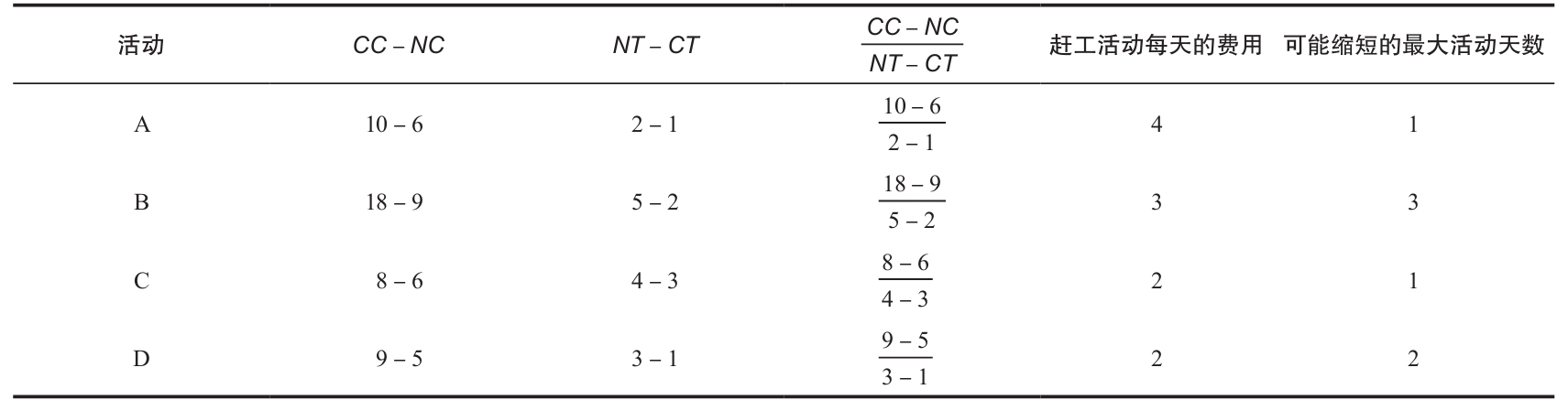
（3）計算關鍵路徑。 對於我們使用的簡單網絡圖，這個項目計劃花費10天時間，其關鍵路徑是A-B-D。
（4）用最少的費用來縮短關鍵路徑的完工時間。 最簡單的辦法是從初始計劃入手，找到關鍵路徑，將關鍵路徑上趕工費用率最低的活動的完工時間減少一天，然後重新計算並尋找新的關鍵路徑，在新的關鍵路徑上同樣逐次逐日減少完工時間。重複這一步驟，直到獲得滿意的完工時間或完工時間不能進一步縮短為止。表4-3顯示了逐次逐日減少完工時間的過程。
表4-3 在常規工作時間內逐次逐日縮短項目的完工時間
①為了在關鍵路徑上縮短1天，可以單獨縮短活動A，或者同時縮短活動B和C（僅僅修改關鍵路徑上的活動B或C不能縮短時間）。
②活動B和C必須同時趕工才能縮短1天時間。
③縮短活動B不能縮短項目的時間長度，所以這個額外的費用不會產生。
以表4-3來開展工作一開始看起來會很困難。在第1行中，所有的活動都是常規時間和常規費用。關鍵路徑是A-B-D，完成項目的費用是26美元，項目完工時間是10天。
第2行的目的是把項目的完工時間減少1天。我們知道必須在關鍵路徑上減少一項或多項活動的時間。在第2列中，我們注意到活動A可以減少1天（從2天變為1天），活動B可以減少3天（從5天變為2天），活動D可以減少2天（從3天變為1天）。再後面一列顯示了每項活動時間減少一天所增加的成本。例如，對活動A，它的常規費用是6美元，在2天內完成。如果它可以在1天內完成，則費用是10美元，增加了4美元。因此，我們認為使活動A完工時間減少一天的費用是4美元。對活動B，它的常規費用是9美元，在5天內完成。如果讓它在2天內完成，其費用是18美元。因此活動B完工時間減少3天的費用是9美元，或減少1天的費用是3美元。對於C，它的常規費用是5美元，在3天內完成。如果它在1天內完成，則其費用是9美元。因此活動C完工時間減少2天的費用是4美元（即減少1天的成本是2美元）。在時間上減少1天費用最低的是活動D，費用是2美元。所以整個網絡的費用上升到28美元，而項目的完工時間減少到9天。
我們下一步的迭代開始於第3行，目標是把項目的完工時間減少到8天。9天的關鍵路徑是A-B-D。我們可以縮短活動A 1天、B 3天、D 1天（注意：活動D已經從3天減少到2天了）。把每個活動減少1天所產生的費用與第二條路徑相同。接著，活動時間減少費用最小的是活動D。活動D的時間從2天減少到1天使得在網絡中所有活動總費用上升到30美元，而項目的完成時間下降到8天。
第4行與第3行相同，只是現在在關鍵路徑中只有活動A和B的活動時間可以減少。結果活動B的時間減少，使得總費用上升到33美元，增加了3美元，而項目的活動時間縮短為7天。
在第5行（實際上是我們解決問題的第5次迭代），活動A、B、C和D都在關鍵路徑中，D不能再減少，因此，我們只能選擇活動A、B和C。注意活動B和C是並行的，因此，減少活動B而不減少C是沒用的。我們的選擇是單獨減少活動A，其費用是4美元/天，同時減少活動B和C的費用是5美元/天（B是3美元，C是2美元），因此，在這次迭代中我們減少活動A。
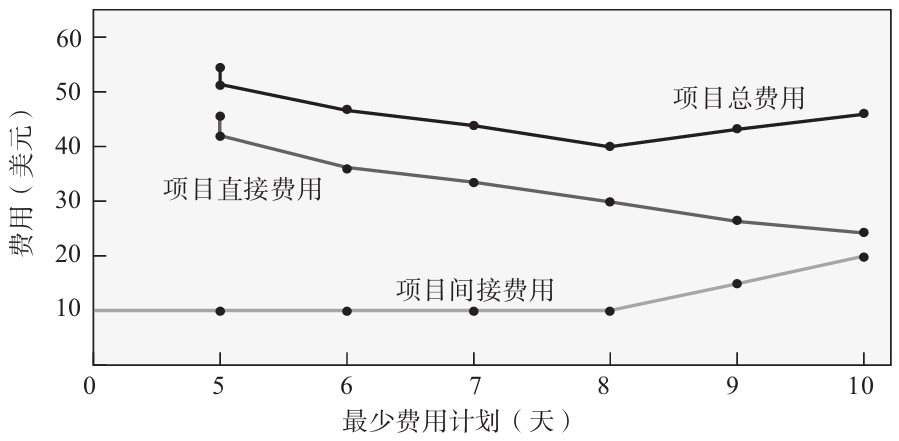
圖4-8 最少費用計劃與成本圖例
在第6行，我們考慮選擇在第5行時所考慮到的活動B和C。最後，在第7行，我們唯一的選擇是減少活動B的天數。由於活動B和C是平行的，並且我們不能減少活動C，所以，單獨減少活動B也沒有實際價值。我們不能再進一步減少項目的完工時間。
（5）繪製項目直接費用、間接費用及總費用的曲線，制訂最少費用計劃。 圖4-8所示的是前8天每天是一個固定成本10美元，以後每天增加5美元情況下的間接費用曲線。直接成本標示在表4-3中，項目的總費用是這兩個費用之和。
每天的直接費用與間接費用求和就得到總費用曲線。我們可以看出，該曲線的最小值出現在完工時間為8天的計劃中，其值為40美元=直接成本（30美元）+間接成本（10美元）。
[1] 1盎司=28.35克。——譯者注