e5 黄達 金融學 v3
第五節 無套利均衡與風險中性定價
關於金融市場的均衡
市場的大系統中有商品服務市場、有勞動力市場、有資金借貸市場、有本章講的資本市場等等。商品服務市場有供給與需求的對比並從而形成商品和服務的均衡價格,勞動力市場有供給與需求的對比並從而形成均衡工資率,資金借貸市場有供給與需求的對比並從而形成均衡利率。本章講的資本市場上有種種金融工具,那麼,這裡的供需與均衡應該怎樣理解和把握?
關於這個問題的一個重要視角、重要理論是:無套利均衡(no-arbitrage equilibrium)及其均衡價格(equilibrium price)定價模型。
本節只是作極其簡略的介紹。
金融產品的可替代性
在第八章第一節講了金融產品的特徵,那是從五個方面講的。較為簡練的概括就是“三性”:流動性、風險性和收益性。如果用商品的使用價值類比,所有金融產品的“使用價值”更會集中於一點,即都是對未來收益的所有權、要求權、索償權,都可視為各產品未來的收入現金流——由流動性能、風險大小、收益高低等因素所決定的未來收入現金流。而取得未來現金流的能力也就是金融產品的“價值”所在。
林林總總的普通商品,使用價值各異,總的說來不具有置換性,只有在同類品種內的極其狹小範圍之間有可能相互代替。而金融產品雖然也是林林總總、多種多樣,卻由於有著共同的單一“使用價值”,可以直接相互比較。所以,凡是可以取得同等未來收入現金流的金融產品,它們就會被認為是等同的;那麼彼此之間也就可以互相替代。可以相互替代的金融產品,也就應該認定有等量的價值。
複製與無套利均衡分析
精確一點地說,作為兩個未來的收入現金流,只要在任何可能發生的場合,所發生的現金流量相等,則兩個現金流所代表的兩項金融產品就是完全等價的。
自然,要找出一對一的兩種金融產品,未來的現金流完全等同,從而兩者可以視為全然等價,幾乎是不可能的。但只要引進資產組合,這種顯得苛刻的要求則可以實現。那就是,在金融市場中選取一項金融產品,如果可以找到另外一些金融產品,按適當的比重把它們組合起來,得到的組合在未來任何情況下所產生的現金流都與選取的這項金融產品未來的現金流完全相同,則選取的這項金融產品與這組金融產品的組合就是完全等價的。也可以說,這組金融產品的組合成為選取的這項金融產品的複製品;而選取的這項金融產品就是這個組合的被複製品。
等價的被複製品與複製品,它們的價格應該相等。如果不相等,就會出現無風險的套利機會。當存在這樣的機會時,可以對價格低者做多頭(long position),對價格高者做空頭(short position);多頭買進與空頭賣出的差價就是無風險地套取到的利潤——相當於無風險收益率的收益。這樣的操作之所以無風險,是因為多頭與空頭二者未來的現金流在任何情況下都完全相同:對空頭承擔的未來償付現金流的責任完全可以用多頭在未來獲得的收入現金流來抵補;對多頭承擔的未來償付現金流的責任則完全可以用空頭在未來獲得的收入現金流來抵補。
可舉例說明:有某一種股票,對該種股票可以通過購入某一無風險資產並同時購買該股票遠期合約的方式,實現對該股票的複製。假設無風險利率為5%。如以105元的遠期價格買入該種股票1股的遠期合約,同時以100元購入1年後到期、面值為105元的國債,這就等同於現在以100元購入該種股票並予以持有。如表23—3所示,複製品和被複製品的即期和遠期現金流完全一致;表中的S為1年後該股票的價格。
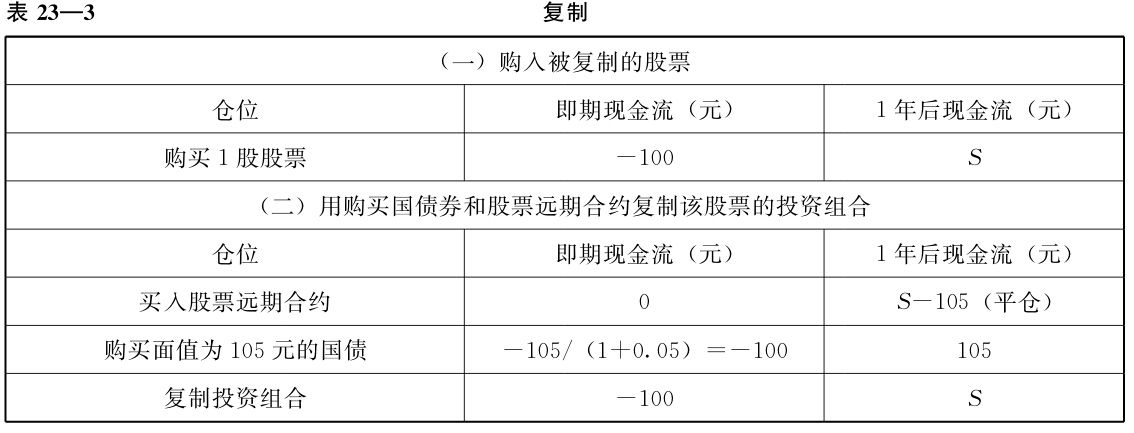
如果其中某一資產的價格發生偏離,可以構建無風險套利頭寸。例如,在上述其他條件不變的情況下,如果股票的價格為104元,就存在無風險套利的機會,可以:(1)借入股票賣空;(2)買入該股票的遠期合約;(3)以100元購入1年後到期、面值為105元的國債,並從而實現4元的無風險套利收益——如表23—4所示,當期可以得到4元的淨現金流入。1年後,國債投資資金回收,數額為105元,加上股票遠期合約平倉收益或損失S-105元,兩者之和恰恰可以用於購買並歸還借入的股票。
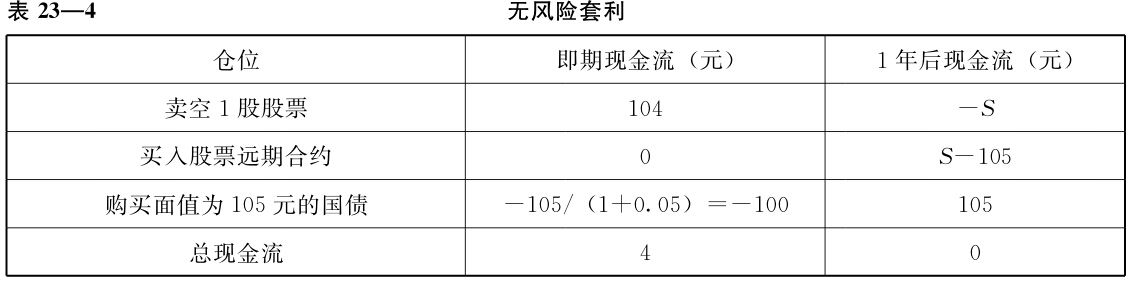
當然,理論上的論述,套利應是無風險的。但在實際運作中,因為市場存在摩擦,如需要交易費用,如交易有時間差等,不可能完全無風險。
套利機會的出現意味著複製品和被複製品任一方的市場價格或雙方的市場價格處於失衡狀態,套利力量將使價格復位;價格復位,套利機會也同時消失。因此,不存在套利機會的金融產品的市場價格意味著均衡價格。這樣的分析思路稱為無套利(機會的)均衡分析。
其中,複製技術是關鍵。
複製技術
現以著名的布萊克斯科爾斯期權定價公式為例來說明覆制技術。我們已經知道,公式(23·33)中左邊的c(t)是歐式看漲期權在到期日前t時刻的市場價格,右邊實際上是它的複製組合。N(d2)前面的負號表示在這個複製組合中無風險證券是空頭(即相當於以無風險利率借入現金)。
這個公式實際表明,作為相關資產的股票和無風險證券按一定比例的數量組合起來,就能複製買權。而股票的數量和無風險證券的數量隨著時間的變化不斷地進行調整,才能保持對買權的等價複製關係,這稱為“動態複製”(dynamic replication)。
等式成立,意味著左右兩邊直至到期日之際所產生的現金流在任何情況下都相同(我們已經知道,歐式期權在到期日前是不執行的);等式兩邊一旦不相等,就意味著出現無風險套利的機會。所以,複製和無風險套利在這個意義上是緊密相連的。其實,所有的衍生品定價技術在本質上都是複製套利定價。
上面所述的被複製品是單個金融商品,複製品是一組金融商品。因為兩者是完全等價的,所以前者可以看做後者的“組合”,而後者就成為前者的“分解”。“組合”與“分解”技術是金融工程的核心技術,通過一定的技術手段對現有的金融商品加以組合和分解,可以創造出許許多多新型金融商品,這是金融工具創新的基本手段,其原理則是複製套利。
金融市場均衡的特點
通過套利,消除無風險套利機會,如此建立的均衡與一般商品及服務市場的供需均衡相比有其顯著的特殊性。
金融基本的內涵是借貸,這蘊涵著金融市場具有“空頭”的機制。通常說的“買空”是先買進商品,以後再拋售平倉。價格上漲就能獲利,否則反之。通常說的“賣空”是先賣出商品,以後再補進平倉。價格下跌就能獲利,否則反之。不論是買空還是賣空,之所以標之以“空”,是因為買時並未付出現款,賣時並未拿出現貨。如果與借入現款來購買金融產品比較,“買空”是以負債的義務持有金融產品;如果與借入金融產品出售比較,“賣空”則是以負債義務持有應收權利。所以“空頭”頭寸就意味著在平倉之前的負債金額。在這裡,借貸和“做空—建立空頭頭寸”,在本質上是同一回事。而套利就是在借貸這個基礎平臺之上對買空與賣空的結合運作。
這就產生了套利均衡機制與一般商品和服務市場供需均衡機制之間的顯著不同特點。
第一,是空頭機制的作用。對於價格被低估的金融產品或複製組合,套利者將建立現金空頭大量購入,從而產生巨大的需求;對於價格被高估的複製組合或金融產品,套利者將建立證券空頭大量出售,從而產生巨大的供給。因為套利是無風險的,所以無論是現金空頭還是證券空頭的資本成本都很低,即只要求無風險回報率。這樣,套利者將傾向於無限放大套利頭寸。這就會產生巨大的供需壓力,並使失衡的價格迅速復位。
第二,在於建立均衡過程中參與者的情況不同。在一般的商品和服務市場中,一旦價格失衡,眾多的供給者和需求者都會採取行動,但每位供給者和需求者都只會少量地調整自己的供給量和需求量,市場將他們的調整集結起來,才會產生大的供需量的調整,從而推動價格復位。套利則不然,一旦發現套利機會,只需要少數套利者,在理論上說甚至只需要一位,就可以利用空頭機制建立巨大的套利頭寸來推動失衡的價格復位。因此,套利重建均衡的速度遠高於一般商品和服務市場供需缺口的調整。
風險中性定價
套利使金融產品實現均衡價格,也即意味著市場價格復歸於價值。無套利均衡分析的定價模型也是直接採用折現公式建立的。
第二節討論了幾種金融產品未來收入現金流的折現值公式。其中,股票折現值的公式(23·15)具有一般的意義。把公式(23·15)進一步一般化,可以是:

在這個折現公式中,首先是r的值如何認定。
在資本資產定價模型中,核心在於選取與風險相匹配的貼現率r。這構成第三節的內容。但無套利均衡分析認為,涉及風險補償的折現率是難以找到的。比如,對於風險補償,因人而異。理性的投資者被認為是風險規避者(即風險厭惡者),但各人厭惡風險的程度也還不一樣。相比較而言,風險厭惡越甚(即越保守)的人,對於同樣的風險所要求的風險補償就會比較高;反之亦然。因為人們的風險偏好(厭惡)程度不同,從而不同的人所要求的風險補償也不同,這就無法找到一個可以代入折現公式的統一的、共同的折現率。
於是設想,在一個假想的世界裡,人們對風險普遍採取無所謂的態度,即他們在承擔風險時,不管風險大小如何,都不要求風險補償。同時,他們也不像賭徒那樣為了追逐風險,寧可付出風險折扣。這樣的人可稱為風險中性(risk neutral)的人。理性的投資者被認為是風險厭惡(risk averse)的,賭徒被認為是風險偏好(risk preference)的,風險中性的人則正好嚴格地介於二者之間。由風險中性的人所構成的假想世界可稱為風險中性的世界。
在這個假想的風險中性的世界裡,因為人們風險偏好不同而無法確定一個統一折現率的難題不存在了;對於任何現金流,都可以統一地採用無風險利率——既不含風險補償也不含風險折扣的利率作為折現率。
再者,是對未來預期的收入現金流如何計算。無套利均衡分析認為,對未來可能發生的各種情況下的現金流的概率分佈,在風險中性的世界裡也會不同於真實世界的概率分佈,而應是一個風險中性概率。
對於一個金融市場來說,風險中性概率是否存在?如果存在,是否唯一?如果存在而不唯一,會發生什麼情況?又如何處理?論證的基本原理是:(1)存在風險中性概率的必要且充分條件是市場中不存在無風險套利機會。(2)風險中性概率是唯一的,其必要且充分條件是市場是動態完全的,而所謂“動態完全”是指市場中有足夠多的金融商品可以充當構築動態複製組合的零部件。(3)在實際的市場並非動態完全的條件下,可以創造出原來“缺失”的新的金融產品並從而補足市場的完全性。
這樣,在假想的風險中性世界裡的折現公式是:

問題是,以這樣的方式計算得到的假想世界裡的現金流的價值拿回到真實世界裡,是否就是該現金流所代表的金融產品的價值?或者說,是否就是無套利均衡價格?
邏輯的推理是:當套利機會出現時,因為它給予人們無風險套取利潤的機會,所以不管發現套利機會的人的風險偏好如何,都會採取套利行動。這就是說,套利活動與人的風險偏好(厭惡)是無關的;消除套利機會後的均衡價位也應是與人的風險偏好(厭惡)無關的。既然可以認為無套利均衡價格就應該是現金流的折現值,在假想的風險中性的世界裡得到的折現值在真實世界裡也就應該依然有效。
根據以上思路來計算均衡價格,被稱為風險中性定價(risk-neutral pricing)。在實踐中,對於這一定價技術所依據的原理作了更簡明的歸納:
(1)所有證券的預期收益率均為無風險利率。
(2)無風險利率是任何預期的未來現金流最為適當的折現率。
風險中性定價在國外大型投資銀行的新產品創新中經常使用。
【複習思考題】
1.種種金融工具的交易,幾乎都不按票面值進行,為什麼?你是否知道鈔票也有不按票面計價的情況?
2.下面哪種證券具有較高的實際年利率?
(1)票面金額為100000元,售價為97645元的3個月期限的國庫券。
(2)售價為票面金額,每半年付息一次,息票率為10%的債券。
3.某公司發行5年到期的債券,票面面額為1000元,售價為960元,年息票率為7%,半年付息一次。試計算:
(1)當期收益率。
(2)到期收益率。
(3)持有3年後,將該債券以992元的價格出售,則該投資者的實際收益率為多少?
4.對於金融資產——無論是原生工具還是衍生工具——的評估,都提到“內在價值”這個概念。這個概念的本質內涵是什麼?
5.如何理解金融資產的收益與風險的對稱原則?試通過對一些金融工具特徵的簡要分析,來表達你對這一問題的理解。
6.對於金融資產的風險大小和收益高低,人們早就憑藉經驗進行估計,並懂得對資產進行“選擇”和“組合”。為什麼說只有當對風險的科學度量成為可能,才有資產組合理論和資產定價模型理論的發展?
7.也許你過去聽到過期權定價模型獲得了諾貝爾經濟學獎。對於這個定價模型的貢獻,人們是怎樣估價的?
8.有人說,金融市場的均衡就是由無套利均衡體現的。你對這樣的論斷是怎樣領會的?
9.風險客觀存在,但可以推導出風險中性定價。對於推導的基本思路,你能理解到怎樣的程度?