e5 黄達 金融學 v3
第四節 期權定價模型
期權價格與期權定價模型
期權這種衍生金融產品的價值體現為期權費(option premium),即期權的買主按特定價格從期權的賣主買進期權所支付的款項。期權費的多少就是期權的價格;行文中也有期權費價格(option premium prices)的說法。
期權費包含兩部分內容:內在價值(intrinsic value)與時間價值(time value)。
在期權領域中,內在價值的術語是專指:期權相關資產的市場價格與執行價格,也叫履約價格(strike price,exercise price)兩者之間的差額。對於看漲期權來說,內在價值等於市場價格大於執行價格的部分。例如,一種作為期權合約的股票,其執行價格是50美元,市場價格是52美元,則該股票的內在價值就是2美元。對於看跌期權來說,內在價值等於市場價格小於執行價格的部分。例如,一種作為期權合約的股票,其執行價格是52美元,市場價格是50美元,則該股票的內在價值也是2美元。市場價格與執行價格的差越大,期權的內在價值就越大。內在價值是期權費的核心部分。
期權的時間價值,是指期權費超過其內在價值的部分。在美式期權中,隨著期權的有效期限的加長,期權的價值會隨之加大。之所以如此,有這樣的解釋:比較其他條件相同只有到期日不同的兩隻期權,有效期長的期權,其執行的機會包含了有效期短的期權所可能有的執行合約的機會;而有效期短的期權,則不可能有超過自己的有效期卻處於有效期長的期權在其到期日之前所具有的執行合約的機會。
期權定價的理論模型,是在期權交易實踐存在很久之後於1973年問世的。在這方面作出重要貢獻的是費希爾·布萊克(Fischer Black)、邁倫·斯科爾斯(Myron Scholes)和羅伯特·默頓(Robert C.Merton)。斯科爾斯和默頓也因此獲得了1997年的諾貝爾經濟學獎。[1]解決了期權這種資產的定價方法,對於現代金融理論和實踐的發展有重大意義。
按照期權的運作原理,對於購買期權者來說,期權的內在價值不會小於零。按美式期權,看漲期權Call(call option)的價值區間是:

式中,P為相關資產在合約執行時的市場價格;S為執行價格。
按照歐式期權,上面公式中的“≥”符號需要改成“=”符號。
期權價值的邊界只給出了一個價值變化區間,要得到具體的數量值,還需要藉助於不斷髮展的期權定價模型。到目前為止,有關的研究又有很大進展。但在說明基本原理時,還需要從最簡單的二叉樹定價方法開始。在本教材中,也僅限於用通俗的方式講解這方面的最基本原理。
期權定價的二叉樹模型
為了給期權定價,需要設計一個對衝型的資產組合(hedge portfolios)。設計的對衝型資產組合包括:(1)需要買進一定量的現貨資產;(2)賣出一份看漲期權(為了簡化,以下均就歐式期權討論),該期權的相關資產就是買入的那種現貨資產;(3)買入現貨的量必須足以保證這個組合的投資收益率相當於無風險利率,從而使投資成為可以取得無風險利率收益的零風險投資。
先舉一個具體例子:
假定某資產的當前市場價格是80元,預期一年以後價格可能上升到100元,也可能下降到70元。同時假定市場上現在有這種資產的看漲期權,期限一年,執行價格是80元,恰好等於當前的市場價格。這時,投資者可以買入該資產的2/3,為此要付出53.33元(=80×2/3);同時賣出一份看漲期權,並從而有一筆期權費收入C,即看漲期權的當前價格。兩者相抵,實際的投資額為53.33元-C。
當資產的價格一年以後上升到100元時,期權買方會行權,即按照約定的80元價格要求投資者出售資產。由於投資者手中只有該資產的2/3,所以還得按100元的市場價格從市場上購買不足的1/3用於交貨,支付的金額是33.33元;同時,得到80元的資產銷售收入。在買賣合約和執行合約時,投資者的支出總額是86.67元-C[=(53.33-C)+33.33]。[2]如果暫不考慮C,投資者虧損6.67元(=86.67-80)。
假如一年後資產的市場價格下降到70元,期權買方不會行權。這時,投資者的資產價值——起初買入該資產2/3的買入價值——要相應貶低。如果不考慮C,投資者虧損6.67元[=(80-70)×2/3],即與資產的市場價格上漲到100元時所虧的數量一樣。
之所以不管資產的價格是漲是跌都會出現同樣的結果,顯然是由於在出售看漲期權合約的同時購買了2/3數量的同一種資產的現貨,並從而起了對衝作用。
考慮到有期權費收入C,可能不虧。由於不管資產的價格是漲是跌都虧6.67元,所以從平衡虧損的角度考慮C,C的決定是與資產價格的漲跌無關的。但還有一筆收益是必須加以考慮的,那就是投資應取得的無風險利率的收益。假設無風險利率是10%,則應有的收益是(53.33-C)×10%。如果C滿足下式:
C=6.67+(53.33-C)×10%
即C等於10.91元,則投資者的投資行為是零風險的。
分析到這裡可以看出,為了建立對衝組合,每出售一份看漲期權合約的同時需要購買一定比例的同一種資產的現貨,這個比例叫做對衝比率。例子中的對衝比率是2/3。正是對衝比率足以保證組合的投資收益率相當於無風險利率。
以下推導如何確定對衝比率,並從而確定期權價值的方法。
就看漲期權——而且是歐式期權——討論,假設P0為期權合約中資產的當前價格;u為該資產到合約執行時價格上升的幅度;d為該資產到合約執行時價格下降的幅度;r為時間為1期的無風險利率;C為看漲期權的當前價格;Cu為資產價格上升時的看漲期權內在價值;Cd為資產價格下降時的看漲期權內在價值;S為看漲期權的執行價格;H為對衝比率。

一旦知道了對衝比率H,就可以進一步求出看漲期權的價格C。
由於這個無風險投資組合的投資成本是HP0-C,按照無風險利率r計算,所投本金的未來價值應該是(1+r)(HP0-C),並且等於到期時資產的價值uHP0-Cu或者dHP0-Cd。因為uHP0-Cu=dHP0-Cd,可任取其一。如取價格上漲時的資產價值表達式,於是,有
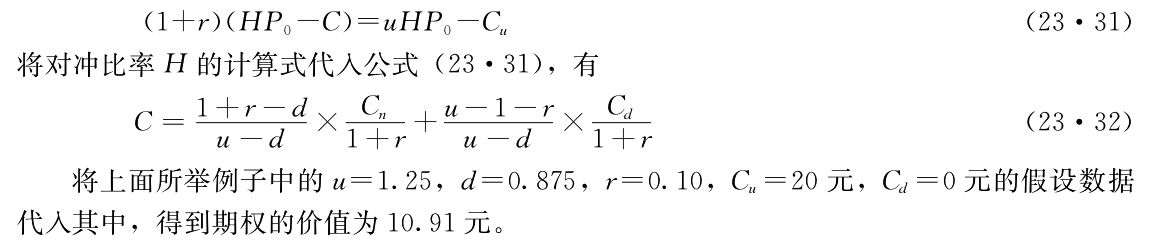
以上為期權定價的方法稱為二叉樹模型。之所以如此稱謂,是由於論證出發點的基本要素可以由圖23—5形象地表達出來。
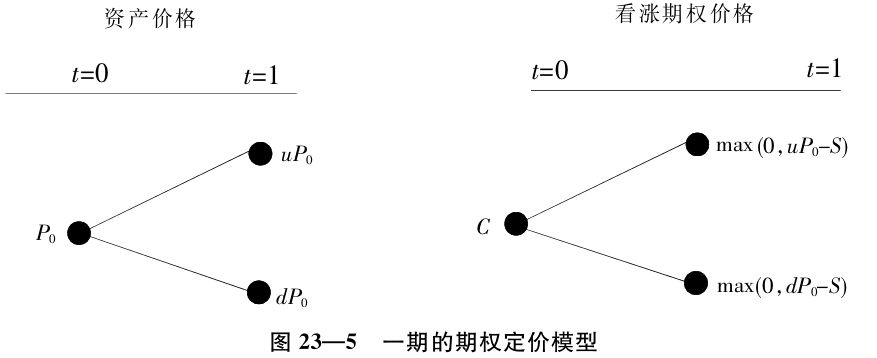
我們上面分析了一個投資期只有一期的極其簡單的情形。現實情況複雜得多。比如投資期不止一期,而是兩期、三期、…,但基本原理還是一樣的。
布萊克斯科爾斯定價模型
布萊克與斯科爾斯的最大貢獻,是導出一個相對簡單的方程,使其能夠在廣泛的情況下對期權定價。對它的論證是有關專門學科的內容,下面僅作簡單提示。
布萊克斯科爾斯定價模型假定期權是歐式看漲期權;價格可以在期間內連續變動;無風險利率在期間內不發生變化;假設相關資產為股票,股票沒有現金和利息等分紅收入。該定價模型可表示為:

式中,第一個因素和第四個因素是可觀察的市場因素,第二個因素和第三個因素是合約本身定義的,只有第五個因素σ需要對價格波動進行統計分析。
註釋
[1]布萊克於1995年逝世。
[2]因四捨五入原因,此處取實際值86.67元。